Диаграммы Фейнмана – наглядный и универсальный графический способ изображения взаимодействий частиц, дополненный алгоритмом расчёта вероятности этих взаимодействий. Метод диаграмм предложен Р. Фейнманом в 1949 г. и является наиболее широко используемым методом описания взаимодействий частиц в квантовой теории поля.

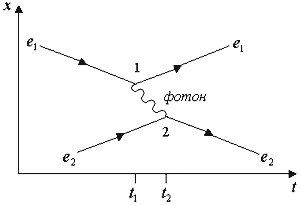Простейшая диаграмма Фейнмана для рассеяния электронов.

Диаграммы Фейнмана показывают, как произошло взаимодействие между частицами. На диаграммах частицы изображаются линиями, а точки (вершины), из которых выходят эти линии (или в которые приходят), показывают места локальных взаимодействий частиц. Рассмотрим простейшую диаграмму рассеяния двух электронов за счёт электромагнитного взаимодействия. Процесс развивается в пространстве и во времени. Ось времени t направлена слева направо. Координатная ось х, условно отражающая положение частиц в пространстве, направлена снизу вверх (эти оси на диаграммах обычно не показывают). Диаграмма “читается” следующим образом. До взаимодействия (t < t₁) имелись два свободных сближающихся электрона е₁ и е₂. Им отвечают незамкнутые слева линии. Взаимодействие между ними произошло в период времени t₁ – t₂. В точке (вершине) 1, отвечающей моменту t₁, электрон е₁ испустил фотон (переносчик электромагнитного взаимодействия) и, испытав отдачу, изменил направление движения. Фотон, изображённый волнистой линией, распространяется в сторону электрона е₂ и в точке (вершине) 2 в момент времени t₂ поглощается им. Электрон е₂, испытав отдачу, также изменяет направление движения. Далее электроны разлетаются, не испытав больше никаких взаимодействий. Каждому элементу диаграммы отвечает известная функция или множитель, которые по известным правилам объединяются в математическое выражение, дающее вероятность процесса. Линиям со свободными электронами, приходящим из t = -∞ и уходящим в t = +∞, отвечают реальные частицы. Внутренним линиям отвечают виртуальные частицы, распространяющиеся от точки рождения до точки поглощения (в данном случае это виртуальный фотон). Приведённая диаграмма показывает самый простой вариант электрон-электронного рассеяния. Для получения полной вероятности этого процесса необходимо учесть все возможные диаграммы, которые могут иметь очень разветвлённую структуру.

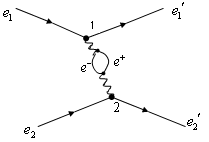     Пример одной из таких более сложных диаграмм рассеяния показан на рис. справа. В случае электромагнитного взаимодействия константа взаимодействия мала, поэтому диаграммы, содержащие большее число вершин, дают малые поправки по сравнению с вкладом основной диаграммы. Диаграмма, имеющая n вершин, при прочих равных условиях будет давать вклад в амплитуду процесса в 10ⁿ раз меньший, чем амплитуда элементарного процесса

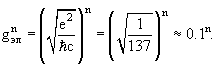
Сечение процесса, содержащего n узлов, пропорционально квадрату амплитуды, т.е. . Диаграммы Фейнмана используются также для наглядного описания процессов, обусловленных другими типами взаимодействий.

См. также

• Диаграммы Фейнмана
• Диаграммы Фейнмана
• Диаграммы Фейнмана
• Диаграммы Фейнмана
• Механизм взаимодействия частиц
• Диаграммы Фейнмана