Распределение Гаусса  (нормальное распределение) − плотность распределения вероятностей случайной величины n.

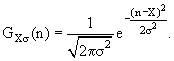
    Функция G_Xσ называется функцией Гаусса. Говорят, что результаты измерений имеют нормальное распределение, если они описываются функцией Гаусса. Распределение Гаусса, в отличие от распределения Пуассона, характеризуется двумя независимыми параметрами X и σ. X − среднее число отсчетов, которое мы ожидаем получить в случае многократного повторения измерений. σ − среднее стандартное отклонение.
    Оказывается, что если на результаты измерений влияет большое число источников небольших случайных ошибок, то вся совокупность измерений имеет в качестве предельного распределения симметричную колоколообразную функцию Гаусса. Центр распределения X, совпадающий с его максимумом, будет истинным значением измеряемой величины.
Распределение Гаусса нормировано на единицу.

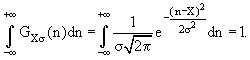
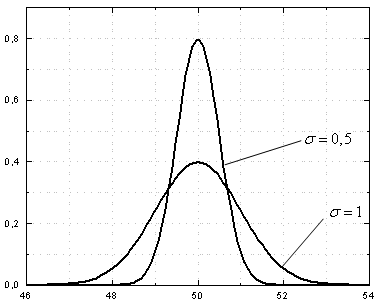
Рис. 1. Распределение Гаусса для σ = 0,5, X = 50 и σ = 1, X = 50.

    На рис. 1 показано два нормальных или гауссовых распределения, соответствующие различным измерениям с одинаковыми значениями X и разными σ. В первом случае X = 50, σ = 0.5, во втором случае − X = 50, σ = 1. Величина σ в знаменателе экспоненты обеспечивает для более узкого распределения большую высоту в максимуме.
    В случае распределения Гаусса ожидаемое среднее значение для большого числа измерений можно вычислить по стандартной формуле

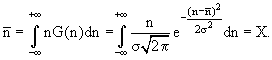
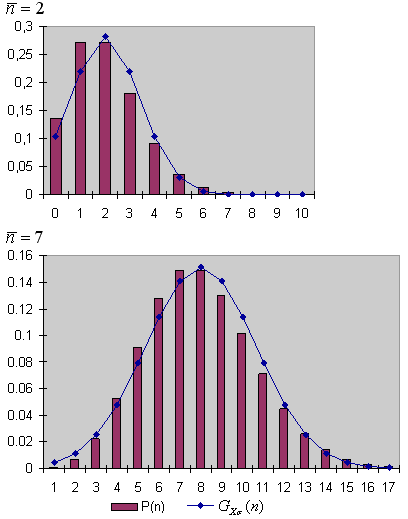
Рис. 2 Сравнение распределений Пуассона P(n) и Гаусса G_Xσ(n) для = 2 и = 7.

    Сравним распределения Гаусса G_Xσ(n) и Пуассона .

1. Распределение Гаусса G_Xσ(n) является непрерывным, т.к. величина n может быть непрерывной, в то время как в распределении Пуассона величина n = 0, 1, 2, 3, … дискретна.

2. Распределение Гаусса G_Xσ(n) определяется двумя параметрами: X − средней величиной и шириной распределения − стандартным отклонением σ, в то время как распределение Пуассона P_μ(n)  определяется единственным параметром
   μ = , т.к. ширина распределения Пуассона σ автоматически определяется величиной μ (σ =  √μ).

3. При увеличении среднего числа отсчетов дискретная природа величины μ в распределении Пуассона P_μ(n) становится менее существенна, и распределение Пуассона хорошо аппроксимируется функцией Гаусса G_Xσ(n).

P_μ(n) ≈ G_Xσ(n),

 при X = μ, σ = √μ.
    На рис. 2 сравниваются распределение Пуассона и распределение Гаусса для двух значений = 2 и X = = 7,  σ =  √7. Видно, что уже при достаточно малых значениях распределения Пуассона и Гаусса практически совпадают. Необходимо иметь в виду, что распределения Пуассона и Гаусса совпадают только тогда, когда для распределения Гаусса σ =  √. В общем случае распределение Гаусса характеризуется двумя независимыми параметрами = и σ. Величина σ может быть как больше √, так и меньше √.