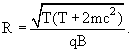Магнитный спектрометр – прибор для измерения импульсов заряженных частиц по кривизне их траекторий в магнитном поле. Магнитный спектрометр характеризуется разрешающей способностью (точностью измерения импульса частицы) и апертурой (диапазоном углов, под которыми должны попадать частицы в спектрометр, чтобы быть зарегистрированными на его выходе). Поясним принцип работы магнитного спектрометра, рассмотрев его простейший вариант.

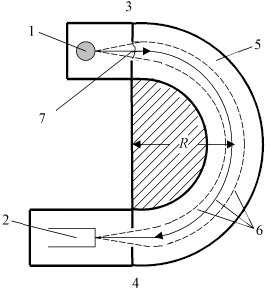Рис. 1. Схема простейшего магнитного спектрометра: 1 - источник заряженных частиц, 2 - детектор частиц, 3, 4 - щелевые диафрагмы, 5 - камера спектрометра, 6 - траектории частиц, 7 - апертурный угол α.

    Спектрометр состоит из источника заряженных частиц 1 (это может быть радиоактивный источник или мишень, где происходит ядерная реакция), полукруговой вакуумной камеры, где создано однородное постоянное магнитное поле напряжённостью Н, силовые линии которого перпендикулярны плоскости рисунка, и детектора частиц 2, регистрирующего частицы, выходящие из камеры. Частицы из источника через щелевую диафрагму 3 попадают в камеру спектрометра. В камере они двигаются по круговым орбитам, радиусы R которых находятся из равенства лоренцевой и центробежной сил: qvH = mv²/R. Отсюда получаем для импульса частицы

Поскольку радиус орбиты частицы R в камере и напряжённость магнитного поля в ней заданы, то в выходную щелевую диафрагму 4 попадут лишь частицы, импульс которых определяется соотношением (1).
    Магнитный спектрометр обладает фокусирующими свойствами, которые проявляются в том, что пучок частиц с одинаковыми импульсами, расходящийся под углом α на входе в камеру, на её выходе будет вновь собираться. Этот угол α и является угловой апертурой спектрометра.
    Изменяя магнитное поле внутри камеры, можно настраивать спектрометр на регистрацию частиц с различными значениями импульса. Поэтому магнитный спектрометр позволяет определять спектр импульсов частиц, вылетающих из источника. Если известна масса частицы, то по импульсу можно определить её кинетическую энергию. Так для нерелятивистской частицы кинетическая энергия Е связана с её импульсом p соотношением

    Радиус кривизны R нерелятивистской частицы массы m, имеющей заряд q и кинетическую энергию T в магнитном поле с индукцией определяется соотношением

Для расчётов удобно использовать соотношение (3) в системе единиц, приведённой в квадратных скобках:

R[м] = (2T[МэВ]mc²[МэВ])^1/2/300B[Тл]Z,

где Z − заряд частицы в единицах элементарного заряда.
    Получим расчётную формулу для движения частицы в постоянном магнитном поле, справедливую при любых скоростях. Сила Лоренца _L, действующая на точечную частицу с зарядом q и скоростью со стороны магнитного поля с индукцией , даётся следующим выражением:

где с − скорость света. Релятивистским уравнением движения в данном случае является Второй закон Ньютона

в котором

− релятивистский импульс, где γ = 1/(1 - v²/c²)^1/2, а m − масса покоя.
    Если в начальный момент времени , траекторией частицы является окружность радиуса R, определяемая величиной B = || и значением кинетической энергии
T = E - mc², где E − полная энергия частицы. Отметим, что T = T(²) = inv, так как в силу соотношений (4) и (5).

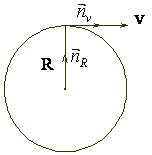Рис. 2. Векторная диаграмма движения частицы в постоянном магнитном поле.

    Обозначим через _v единичный вектор, сонаправленный скорости, через _R − единичный вектор, направленный из центра окружности в точку местоположения частицы. Тогда уравнение движения (5) при учёте (4) сводится к соотношению

Из рис. 2 видно, что

Из (7) и (8) следует, что γmv/R = qB/c, то есть

Формула (9) справедлива как в релятивистском, так и в нерелятивистском случае. Учитывая, что cp = [E² - (mc²)]^1/2 = [T(T + 2mc²)]^1/2, получаем

Введём безразмерный параметр

и Z = q/e, где e − элементарный заряд,

(12)

В нерелятивистском случае (α → 0)

в ультрарелятивистском (α → ∞)

В ультрарелятивистском случае с Z = 1

сравнивая (15) с (14), получаем окончательно расчётную формулу, справедливую при любых скоростях

См. также

• Детекторный комплекс AMS-02
• Структура элементов детектора ATLAS (Магнитная система)