Волновая функция (или вектор состояния) – комплексная функция, описывающая состояние квантовомеханической системы. Её знание позволяет получить максимально полные сведения о системе, принципиально достижимые в микромире. Так с её помощью можно рассчитать все измеряемые физические характеристики системы, вероятность пребывания её в определенном месте пространства и эволюцию во времени. Волновая функция может быть найдена в результате решения волнового уравнения Шредингера.
    Волновая функция ψ(x, y, z, t) ≡ ψ(x,t) точечной бесструктурной частицы является комплексной функцией координат этой частицы и времени. Простейшим примером такой функции является волновая функция свободной частицы с импульсом и полной энергией Е (плоская волна)

.

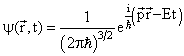    Волновая функция системы А частиц содержит координаты всех частиц: ψ(₁,₂,...,_A,t).
    Квадрат модуля волновой функции отдельной частицы |ψ(,t)|² = ψ*(,t)ψ(,t) дает вероятность обнаружить частицу в момент времени t в точке пространства, описываемой координатами , а именно, |ψ(,t)|²dv ≡ |ψ(x, y, z, t)|²dxdydz это вероятность найти частицу в области пространства объемом dv = dxdydz вокруг точки x, y, z. Аналогично, вероятность найти в момент времени t систему А частиц с координатами ₁,₂,...,_A в элементе объема многомерного пространства дается величиной |ψ(₁,₂,...,_A,t)|²dv₁dv₂...dv_A.
    Волновая функция полностью определяет все физические характеристики квантовой системы. Так среднее наблюдаемое значение физической величины F у системы дается выражением

,

где - оператор этой величины и интегрирование проводится по всей области многомерного пространства.
    В качестве независимых переменных волновой функции вместо координат частиц x, y, z могут быть выбраны их импульсы p_x, p_y, p_z или другие наборы физических величин. Этот выбор зависит от представления (координатного, импульсного или другого).
    Волновая функция ψ(,t) частицы не учитывает ее внутренних характеристик и степеней свободы, т. е. описывает ее движение как целого бесструктурного (точечного) объекта по некой траектории (орбите) в пространстве. Этими внутренними характеристиками частицы могут быть её спин, спиральность, изоспин (для сильновзаимодействующих частиц), цвет (для кварков и глюонов) и некоторые другие. Внутренние характеристики частицы задаются специальной волновой функцией её внутреннего состояния φ. При этом полная волновая функция частицы Ψ может быть представлена в виде произведения функции орбитального движения ψ и внутренней функции φ:

Ψ = φψ,

поскольку обычно внутренние характеристики частицы и её степени свободы, описывающие орбитальное движение, не зависят друг от друга.
     В качестве примера ограничимся случаем, когда единственной внутренней характеристикой, учитываемой функцией , является спин частицы, причем этот спин равен 1/2. Частица с таким спином может пребывать в одном из двух состояний − с проекцией спина на ось z, равной +1/2 (спин вверх), и с проекцией спина на ось z, равной -1/2 (спин вниз). Эту двойственность описывают спиновой функцией взятой в виде двухкомпонентного спинора:

Тогда волновая функция Ψ^+1/2 = χ^+1/2ψ будет описывать движение частицы со спином 1/2, направленным вверх, по траектории, определяемой функцией ψ , а волновая функция Ψ^-1/2 = χ^-1/2ψ будет описывать движение по той же траектории этой же частицы, но со спином, направленным вниз.
    В заключении отметим, что в квантовой механике возможны такие состояния, которые нельзя описать с помощью волновой функции. Такие состояния называют смешанными и их описывают в рамках более сложного подхода, использующего понятие матрицы плотности. Состояния квантовой системы, описываемые волновой функцией, называют чистыми.