Возбуждённые состояния ядер − состояния, в которых энергия системы превышает наименьшее возможное значение энергии, которое называется основным состоянием. Возбуждённое состояние ядра является неустойчивым, и с течением времени ядро переходит в состояние с меньшей энергией возбуждения и в результате таких переходов оказывается в основном состоянии. В оболочечной модели возбужденные состояния ядер возникают в результате переходов нуклонов с низших заполненных состояний на более высокорасположенные по энергии свободные состояния (рис. 1).

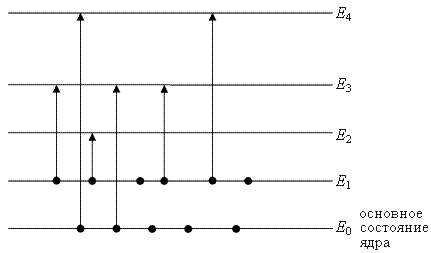Рис. 1. Возбуждённые состояния оболочечной модели.

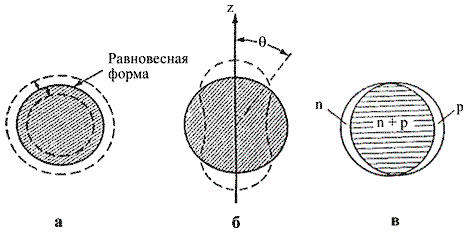Рис. 2. Колебания ядра: а − монопольная объемная мода, б − квадрупольная поверхностная мода, в − нейтрон-протонные поляризационные колебания.

    В атомном ядре наблюдаются возбужденные состояния и другого типа − многонуклонные возбужденные состояния, в которых движение отдельных нуклонов скоррелировано. Это колебательные и вращательные возбуждения атомных ядер (рис. 2–5).
    Когерентные колебания протонов относительно нейтронов называются гигантскими резонансами. Наиболее изученный из них гигантский дипольный резонанс. Он наблюдается во всех ядрах. Феноменологическая теория колебательных состояний атомных ядер была разработана О. Бором (1952 г.).
    Спектры энергий и моментов количества движения возбужденных колебательных состояний дискретны. Энергии квадрупольных и октупольных возбуждений в квантовой теории могут принимать значения

 где n₂, n₃ - числа соответственно квадрупольных и октупольных квантов (для квантов коллективных ядерных колебаний часто используют термин фононы, заимствованный из физики твердого тела), причем n₂, n₃ = 1, 2, 3, ...
    Каждый квадрупольный квант (фонон) имеет момент количества движения J = 2 и положительную четность. Аналогично, каждый октупольный фонон имеет момент
J = 3 и отрицательную четность и т. д. В общем виде энергию возбуждения ядра, в котором одновременно происходят различные поверхностные колебания формы, можно записать в виде

(2)

где n_{J −} число фононов определенного типа, а ћω_J − энергия фонона.
    Формулы (1), (2) лучше всего должны описывать самые низкие колебательные уровни ядер, т. е. уровни, отвечающие n₂, n₃ = 1, 2. Действительно, при увеличении n₂, n₃ во-первых, нарушится гармоничность колебаний, а во-вторых, станут энергетически возможными возбуждения других типов, что усложняет энергетический спектр.

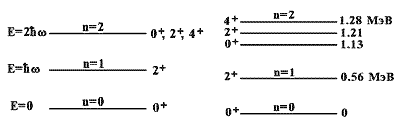На рис. 3 показан спектр низколежащих состояний ядра (справа) в сравнении с идеальным спектром нижних квадрупольных возбуждений чётно-чётного сферического ядра (слева).

    По мере удаления от заполненных оболочек минимум потенциальной энергии ядра может соответствовать деформированному состоянию ядра. У несферического ядра изменяются одночастичные уровни, изменяется частота колебаний, появляются вращательные степени свободы.
    Энергия вращательных состояний четно-четных деформированных аксиально-симметричных ядер описывается соотношением

E = ћ²J(J + 1)/(2),

где − момент инерции ядра, J − спин ядра (рис. 5).

    Модель, которая позволяет одновременно учесть как одночастичные так и коллективные степени свободы ядра — обобщенная модель была развита в начале 50-х годов Д. Рейнуотером, О. Бором и Б. Моттельсоном. В этой модели предполагается сильная связь внешних по отношению к заполненным оболочкам нуклонов с остовом, что может приводить к устойчивой равновесной деформации ядра. Движение остова описывалось в гидродинамической модели. Одночастичные состояния рассчитывались в деформированном потенциале. Впервые такие расчеты одночастичных состояний с использованием деформированного аксиально-симметричного потенциала были выполнены в 1955 году Нильссоном.