Светимость ускорителя − характеристика эффективности системы “ускоритель + мишень”, показывающая сколько актов взаимодействия в секунду происходит между частицами пучка и мишени при единичном сечении этого взаимодействия. Используется как для ускорителей с неподвижными мишенями, так и для ускорителей на встречных пучках (коллайдеров).
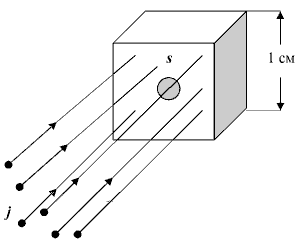 |
Определим светимость ускорителя с неподвижной мишенью. j − плотность потока частиц от ускорителя. Облучаемая мишень − единственное ядро, заключенное в области пространствам размером 1х1х1 см3. Число взаимодействий в секунду частиц пучка с такой мишенью дается соотношением N = jσ, где σ − эффективное сечений. Если теперь перейти к макроскопической мишени, с облучаемой поперечной площадью S, толщиной в направлении движения частиц пучка l и концентрацией ядер (их числом в 1 см3) n, то число взаимодействий в секунду будет определяться выражением
| N = jnSlσ = jМσ, | (1) |
где М − полное число ядер в облучаемой части мишени. Величина L = jМ и есть светимость и вместо (1) можем записать
| N = Lσ. | (2) |
 К понятию “светимость”. Два сталкивающихся сгустка частиц (банча) в коллайдере |
В случае экспериментов на встречных пучках два сталкивающихся
пучка ускоренных частиц являются одновременно и движущимися мишенями. Встречные
пучки состоят из отдельных сгустков частиц, называемых банчами (от
англ. bunch), двигающихся с определенным интервалом (частотой) друг
за другом. Рассмотрим два цилиндрических сгустка одинакового сечения, летящих
навстречу друг другу и затем сталкивающихся.
Будем считать, что сгустки равномерно заполнены частицами и при
столкновении полностью перекрываются. В левом сгустке n1 частиц,
а в правом - n2. Вначале положим, что на орбите коллайдера сгустки
сталкиваются один раз в единицу времени. Число взаимодействий N1
в единицу времени между частицами этих двух сгустков (т. е. число актов
реакций в единицу времени) можно вычислить по формуле (1), приняв левый
сгусток за частицы-снаряды, а правый - за мишень:
| N = jnSlσ = (n1/S)n2σ, | (3) |
Здесь учтено, что плотность потока падающих на правый сгусток частиц левого сгустка j = n1/S, а полное число частиц в правом сгустке (принятом в качестве мишени) n2= nSl, где n - концентрация частиц в правом сгустке. Если сгустки сталкиваются f раз в единицу времени (т. е. с частотой f), то число актов реакции N будет даваться выражением
| N = f(n1n2/S)σ = Lσ, | (4) |
где
| L = f(n1n2/S) | (5) |
и есть светимость коллайдера. Размерность светимости [L] = см-2·с-1. Для исследуемой реакции, имеющей сечение σ, число событий в единицу времени равно N = Lσ.
См. также