Распределение Пуассона  − распределение случайной величины , принимающей целые неотрицательные значения.

Оно определяет вероятность наблюдения величины n в конкретном измерении, если события происходят независимо и характеризуются средней величиной

    Одним из классических примеров распределения Пуассона является распределение числа распадов радиоактивного источника постоянной интенсивности. Распределение Пуассона в этом случае показывает, как распределяются результаты отдельных измерений интенсивности n вокруг среднего значения интенсивности , т.е. вероятность получить значение интенсивности n в данном отдельном измерении, если среднее значение интенсивности равно . Дисперсия D в случае распределения Пуассона равна среднему числу частиц D = . Стандартное отклонение σ = √D = √. С увеличением распределение Пуассона становится всё более симметричным относительно и переходит в распределение Гаусса.

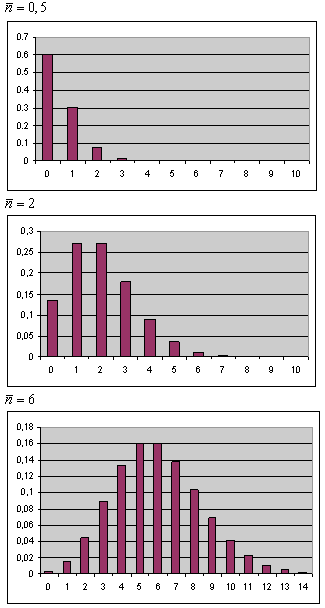
Рис. Распределения Пуассона для = 0.5, = 2 и = 6.