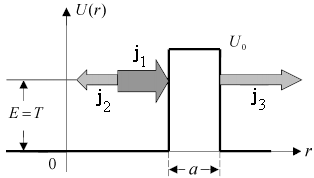
Прямоугольный потенциальный барьер и туннельный эффект: j1 – поток частиц, падающих на барьер, j2 – поток отражённых частиц, j3 – поток прошедших частиц.

    Потенциальный барьер – область пространства, где потенциальная энергия частицы (или тела) выше, чем в соседних областях. Рассмотрим простейший потенциальный барьер прямоугольной формы шириной а и высотой U₀. Вне барьера потенциальная энергия частицы равна нулю. Полная энергия частицы Е равна сумме её кинетической энергии Т и потенциальной U. Вне барьера Е = Т. Если частица двигается на барьер слева и имеет Е = Т < U₀, то с точки зрения классической физики она не может преодолеть его и отразится от него. Действительно, классическая физика требует безусловного сохранения энергии. Если представить, что частица с Е < U₀, вошла внутрь барьера, то она неизбежно должна иметь там отрицательную кинетическую энергию (чтобы её полная энергия сохранилась), что невозможно по смыслу кинетической энергии.
    С точки зрения квантовой физики частица с Е < U₀ может с некоторой вероятностью пройти сквозь барьер. Это явление носит название туннельного эффекта.
    Вероятность прохождения частицы массы m через барьер D определяется соотношением

где .
Основная зависимость коэффициента прохождения D от ширины a и высоты барьера  U₀ определяется экспоненциальным множителем e^-χa.

В случае a ~ 10^-13 см, m ~ 10^-24 г для (U₀ − E) ~ 10 МэВ D ~ 1/e.
То есть частица (протон, α-частица) с заметной вероятностью может пройти сквозь потенциальный барьер, превышающий её энергию на 5–10 МэВ.