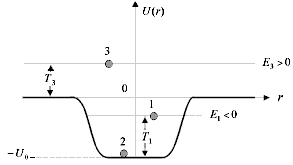
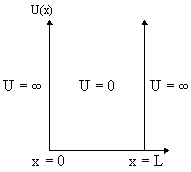Рис. 1. Потенциальная яма

   Потенциальная яма – ограниченная область пространства с пониженной потенциальной энергией частицы. Потенциальная яма обычно отвечает короткодействующим силам притяжения. В области действия этих сил потенциал отрицателен, вне – нулевой.
   Энергия частицы Е есть сумма её кинетической энергии Т  > 0 и потенциальной U (может быть как положительной, так и отрицательной). Если частица находится внутри ямы, то её кинетическая энергия Т₁ меньше глубины ямы U₀, энергия частицы Е₁ = Т₁ + U₁ = Т₁ - U₀ < 0 и частица не может покинуть яму (находится в связанном состоянии). Она двигается в ней с кинетической энергией Т₁, отражаясь от стенок. Если частица находится на дне ямы, то её кинетическая энергия Т₂ = 0 и Е₂ = -U₀ < 0 (частица лежит на дне ямы). Это положение частицы наиболее устойчиво. Если частица вне ямы имела кинетическую энергию Т₃ то она беспрепятственно пересекает яму, преодолевая её с возросшей кинетической энергией Т₃ + U₀.
    В квантовой механике энергия частицы, находящейся в связанном состоянии, может принимать лишь определённые дискретные значения, т.е. существуют дискретные уровни энергии. При этом наинизший (основной) уровень всегда лежит выше дна ямы. По порядку величины расстояние ΔЕ между уровнями частицы массы m в глубокой яме шириной а даётся выражением ΔЕћ²/mа².
    Пример потенциальной ямы – ядерная яма глубиной 40- 50 МэВ и шириной 10^-13–10^-12 см, в которой на различных уровнях находятся нуклоны, двигающиеся со средней кинетической энергией20 МэВ.
    На простом примере движения частицы в одномерной бесконечной прямоугольной яме можно легко увидеть, как возникают дискретные значения энергии. В классическом случае частица, двигаясь от одной стенки к другой, принимает любое значение энергии, в зависимости от сообщенного ей импульса. В квантовой системе ситуация совсем другая. Если движение квантовой частицы происходит в ограниченной области пространства, спектр энергий оказывается дискретным.

    Итак, пусть частица массы m находится в одномерной потенциальной яме бесконечной глубины (рис. 2). Потенциальная энергия U удовлетворяет следующим граничным условиям

При таких граничных условиях частица находится внутри потенциальной ямы 0 < x < L и не может выйти за ее пределы, т.е.

Используя станционарное уравнение Шредингера для случая U = 0, получим

Уравнение (3) описывает положение частицы внутри потенциальной ямы.
    Для бесконечной одномерной потенциальной ямы имеем следующее:

1. Энергия частицы принимает определенные дискретные значения. Обычно говорят, что частица находится в определенных энергетических состояниях. 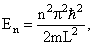где n = 1, 2, 3...
2. Частица может находиться в каком-то одном из множества энергетических состояний.
3. Частица не может иметь энергию равную нулю.
4. Каждому значению энергии E_n соответствует собственная волновая функция ψ_n, описывающая данное состояние.
5. Для собственной функции ψ₁(x) вероятность обнаружить частицу в точке x = L/2 максимальна. Для состояния ψ₂(x) вероятность обнаружения частицы в этой точке равна 0 и так далее.

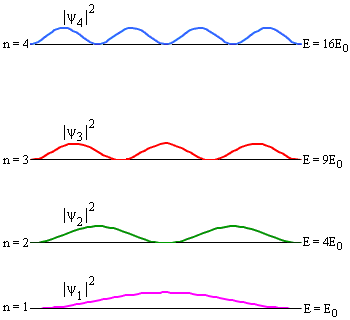
   Рис. 2. Плотности вероятности обнаружения частицы в различных квантовых состояниях.

Подробнее см. "Потенциальная яма" в "Шпаргалке для отличника".