Эксперименты в физике частиц при изучении разных типов взаимодействий

    В основе современных представлений о строении материи лежит глубокий теоретический анализ экспериментальных данных, накопленных в течение последних десятилетий в различных лабораториях мира. Эксперименты проводились с использованием сложнейшей экспериментальной техники.
    Главным инструментом, позволяющим изучить структуру вещества, является ускоритель частиц, создающий частицы столь высокой энергии, что они способны проникнуть в глубинные области изучаемого микрообъекта.
    Ускоритель частиц можно сравнить с микроскопом. Из классической оптики известно, что для изучения структуры объекта, имеющего размер d, его надо облучить светом, длина волны которого λ существенно меньше этого размера, т.е. λ << d. В основе квантовой (волновой) физики, оперирующей с представлением о частице как о волновом пакете, лежит полученное Де Бройлем соотношение между длиной волны λ и импульсом р, который имеет частица: = ћ/р, где ћ = h/2π − постоянная Планка, h = б,б·10^-27 эрг·с. Отсюда следует, что частица имеет тем меньшую длину волны, чем больше ее импульс. Понятно поэтому стремление экспериментаторов построить ускорители, способные ускорять частицы до все более высоких энергий.
    В настоящее время в мире работает несколько таких машин, ускоряющих заряженные частицы (электроны, протоны и антипротоны) до очень высоких энергий. Многие действующие ускорители работают как в режиме выведенных пучков (когда ускоренные частицы направляются на неподвижную мишень), так и в режиме коллайдеров (когда две частицы, ускоренные до высоких энергий, сталкиваются друг с другом).
    Энергетически более выгодным оказывается режим коллайдера, когда сталкиваются два протона, ускоренные до энергии Е₁* и Е₂*. В этом случае суммарная энергия столкновения в системе центра масс Е₁* + Е₂* связана с энергией Е одного из протонов, когда другой неподвижен (т.е. в лабораторной системе), соотношением: Е = (Е₁* + Е₂*)²/2m_р, где m_р ≈ 1 ГэВ/с² − масса протона (1 ГэВ = 10⁹ эВ; 1 эВ = 1.6·10^-19 Дж).
    Впервые коллайдер, в котором сталкивались электроны и позитроны, был построен в Новосибирске (ВЭП-2М). Энергия каждого из пучков была 0.7 ГэВ. С 1994 года энергия электронов и позитронов в Новосибирском коллайдере равна 6 ГэВ (ВЭП-4М).
    В Европейском центре ядерных исследований (ЦЕРН, Швейцария) работает комплекс ускорителей. Сначала был построен протонный синхротрон PS, ускоряющий протоны до энергии ~ 30 ГэВ. Затем ускоритель PS стал использоваться как инжектор для ускорителя SpS. Этот ускоритель некоторое время работал в коллайдерном режиме. Тогда он назывался SppS-коллайдер. Энергия каждого из соударяющихся нуклонов (протона р и антипротона р) на этом ускорителе была равна 315 ГэВ. Далее SpS ускоритель стал ускорять электроны и позитроны и использоваться как инжектор для ускорителя LEP − большого электрон-пози-тронного коллайдера. В каскаде ускорителей (PS, SpS, LEP) ускорялись электроны и позитроны до энергии ~ 100 ГэВ. На рис. 17 изображена схема этого комплекса.

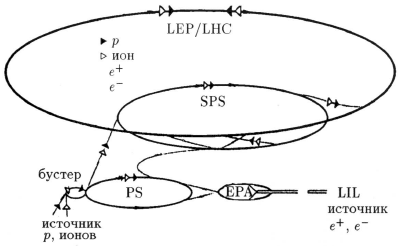
Рис. 17: Схематическое изображение комплекса ускорителей в ЦЕРН.

В 2001 году приостановлены эксперименты на ускорителе LEP и начат монтаж; аппаратуры для нового ускорителя − Большого адронного коллайдера (LHC). Параметры этого ускорителя представлены в табл. 12.

Таблица 12. Параметры коллайдеров высоких энергий: ер, р и рр

Ускорители	HERA (DESY)	SpS (CERN)	TEVATRON (Fermilab)	LHC (CERN)
Начало работы	1992 г.	1981 г.	1987 г.	2008 г.
Соударяющиеся частицы	ер	р	рр	рр	Pb-Pb
Макс, энергия пучка (ТэВ)	е: 0.030 р: 0.02	0.315	1.0	7.0	2.76 ТэВ/н
Светимость (10³⁰ cм^-2с^-1)	14	6	210	1.0·10⁴	0.002
Разрешение по энергии (10^-3)	е: 0.91 р: 0.2	0.35	0.09	0.1	0.1

    В США в Стэнфордской национальной лаборатории (SLAC) на SLC-коллайдере сталкиваются электроны и позитроны каждый с энергией до 50 ГэВ. Кроме коллайдера здесь до недавнего времени работал линейный ускоритель электронов, протяженность ускоряющих элементов которого составляла 3 км. На линейном ускорителе в Стэнфорде были выполнены первые эксперименты по изучению структуры атомных ядер в опытах по рассеянию электронов на ядрах. Эта серия экспериментов закончилась в 50-х годах. Затем в 60-х годах были осуществлены первые измерения структуры протона при рассеянии электронов с энергией ~ 20 ГэВ на неподвижной мишени, состоящей из протонов. В этих опытах было обнаружено, что внутри протона содержится много точечных образований − партонов. Дальнейшее развитие SLAC направлено на изучение В-физики.
    В Германии в крупной лаборатории вблизи Гамбурга сооружен комплекс электронных ускорителей, которые могут работать как в режиме выведенных пучков, так и в коллайдерном режиме. С 1991 года в этой лаборатории начал работать первый в мире электрон-протонный коллайдер: Hadron Electron Ring Accelerator − HERA. На этом ускорителе создана уникальная возможность изучать рассеяние электронов с энергией 30 ГэВ на протонах с энергией 820 ГэВ. В ближайшее десятилетие на этом ускорителе можно будет получать наиболее интересные данные как о структуре микрочастиц, так и о других особенностях процессов взаимодействия.
    Очевидно, что для изучения структуры микрообъектов помимо высоких энергий облучающих частиц желательно, чтобы эти частицы-снаряды были как можно более простыми − бесструктурными образованиями. На современном уровне наших знаний такими частицами являются лептоны: электрон, мюон, τ-лептон и соответствующие им нейтрино. Среди лептонов наиболее доступен для экспериментов электрон. По всем современным экспериментальным данным он не имеет структуры, по крайней мере до расстояний ~ 10^-16 см.
    На рис. 18 представлено, как изменялась во времени ускорительная техника.

Рис. 18: Развитие во времени ускорителей высоких энергий. Значками отмечены действующие ускорители высоких энергий в разные периоды времени. Ускоритель SSC (США) не был построен из-за отсутствия финансирования. Создание ускорителя NLC (соударения е⁺е^-) только планируется.

Опыт по изучению структуры микрообъектов выглядит очень просто. Пробная частица-снаряд (например, электрон) налетает на частицу-мишень (например, атомное ядро) и после взаимодействия с частицей-мишенью регистрируются ее кинематические параметры: энергия, импульс, угол вылета, а также вероятность вылета электрона в элемент телесного угла dΩ = 2πsinθ dθ. Эта вероятность dσ/dΩ называется эффективным сечением процесса. По этим экспериментально измеряемым величинам можно определить, какой импульс q был передан частицей-снарядом при взаимодействии частице-мишени. При упругом рассеянии эту величину легко определить по углу рассеяния θ* в системе центра масс столкновения q = 2р·sin θ*/2, где р − импульс частицы-снаряда.

3.2. Методы измерения поперечных сечений в разных типах взаимодействий

Поперечное сечение, определяющее вероятность процесса, является основной характеристикой процесса взаимодействия.
В ядерной физике все процессы описываются с помощью поперечных сечений. Рассмотрим методы измерения этой характеристики (рис. 19).

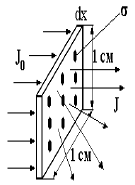Рис. 19. Схема измерения поперечных сечений.

Мишень содержит N [ядер/см³] вещества. Толщина мишени dx содержит N·dx [ядер/см²]. Тогда частицы J₀, падающие на мишень и пересекающие ее, будут выбывать из пучка из-за столкновений, и интенсивность пучка будет изменяться на величину dJ.

dJ = −J₀·σ·N·dx,

где σ·N·dx − доля площади мишени, занятая ядрами. Изменение интенсивности пропорционально J₀·N·dx с коэффициентом пропорциональности σ − эта величина называется ядерным поперечным сечением мишени для частиц пучка. Интенсивность частиц, прошедших без взаимодействия через мишень толщиной х, J(x) = J₀e^-N^σx . Интенсивность частиц, провзаимодействовавших в мишени, J_вз = J₀(l − e^-N^σx).
Величину N·σ = μ называют коэффициентом поглощения, а λ = l/μ средним свободным пробегом. J(x)/J₀ = e^-N^σx = e^-^x/λ.

Поперечное сечение для ядерных мишеней может описывать разные процессы:

а + А → а + А el (упругое рассеяние);
а + А → а + А' + а_i' qel (квазиупругое рассеяние);
а + А → а + А" + b_i inel (неупругое взаимодействие).

На рис. 20 представлены диаграммы Фейнмана для этих процессов. Полное поперечное сечение σ_tot = σ_el + σ_qel + σ_inel.

Можно определить поперечное сечение рассеяния частиц в заданный элемент телесного угла
dΩ(θ,φ)

dΩ = sin θ dθdφ.

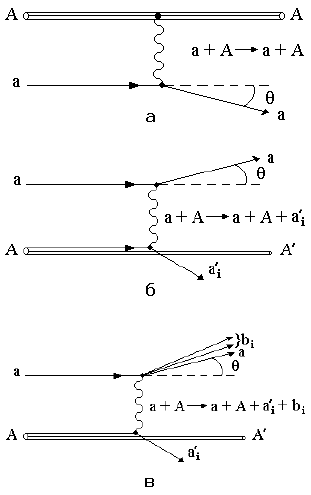
Рис. 20. Диаграммы Фейнмана для рассматриваемых процессов: а − упругое рассеяние; б − квазиупругое рассеяние; в − неупругое рассеяние.

Можно также рассматривать изменение интенсивности пучка в интервале по энергии Е, Е+dE

Дважды дифференциальное поперечное сечение

определяет процесс взаимодействия, в результате которого изменяется угол и энергия частиц после взаимодействия.
Поперечное сечение измеряется в барнах (10^-24 см²), в барнах/стерадиан или в более мелких единицах: мб = 10^-27 см² , мкб = 10^-30 см², пб = 10^-33 см², ...

Все основные эксперименты в ядерной физике сводятся к измерению поперечных сечений, которые характеризуют вероятности процессов взаимодействия.
Способы измерения поперечных сечений сводятся к измерению потоков частиц, упавших на мишень J₀ и прошедших через мишень J(x,θ) (см. рис. 19).

3.3. Методы измерения поперечных сечений в сильных взаимодействиях

3.3.1. Метод пропускающих счетчиков

Этот метод применяется на ускорителях с выведенными на неподвижную мишень пучками. На рис. 21 показана схема расположения детекторов установки для измерения поперечного сечения на ускорителе У70.

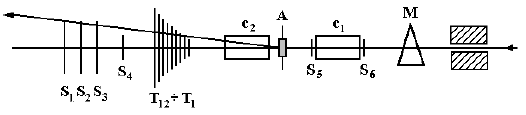
Рис. 21. Схема расположения детекторов на выведенном пучке для измерения поперечных сечений.

Детектор состоит из набора сцинтилляционных S_i счетчиков для мониторирования пучка, черенковских счетчиков с для идентификации частиц с разрешением по скорости Δβ ~ 10^-6, мишени А и системы пропускающих счетчиков (Т1÷T12) разного размера. В эксперименте в Серпухове жидководородная мишень имела длину 3 м и содержала 21 г/см² водорода. Каждый пропускающий счетчик регистрировал частицы в определенном интервале передаваемого импульса |t_i|.
Экспериментальные данные показаны на рис. 22.

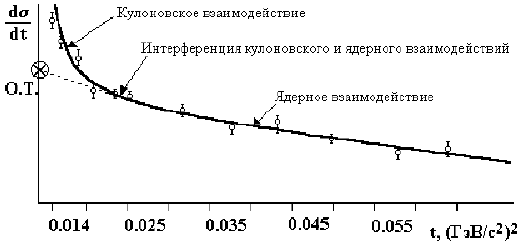
Рис. 22: Дифференциальное сечение взаимодействий в зависимости от квадрата переданного 4-импульса .

Результат аппроксимируется выражением

dσ/dt = |C² + D² + A² + 2CD|

(С − кулоновское взаимодействие; D − действительная часть, А − мнимая часть амплитуды, описывающей ядерное взаимодействие; CD − кулон-ядерная интерференция). Отсюда определяется сечение σ(t_i) = (dσ/d)_t=ti. В разных интервалах t_i работают разные процессы взаимодействия. При
t_i < 0.015 проявляется кулоновское взаимодействие. В области 0.015 < t_i < 0.025 проявляется интерференция кулоновского и ядерного взаимодействий. При t_i > 0.025 работает ядерное взаимодействие. Экстраполируя ход сечения для ядерного взаимодействия к t = 0, получаем оптическую точку (О.Т.).
Далее для определения σ_tot может быть использована оптическая теорема. Оптическая теорема связывает полное сечение с мнимой частью амплитуды упругого рассеяния вперед

где ρ − отношение действительной части к мнимой части амплитуды упругого рассеяния вперед,

ρ = Re ƒ_el(s,0)/Im ƒ_el(s,0), ƒ_el(s,t=0) = D(s,t) + iA(s,t)

Можно определить полное сечение с использованием оптической теоремы другим путем, измеряя число упругих N_el и неупругих N_inel взаимодействий:

N_el + N_inel = σ_tot,

где − светимость, σ_tot − полное сечение.
Оптическая точка (N_el/dt)_t=0 определяется на опыте и связана с полным сечением соотношением

Заменяя σ_tot измеряемыми на опыте величинами N_el и N_inel, получим полное сечение

Способы определения величин (N_el/dt)_t=0, N_el, N_inel зависят от конкретных условий эксперимента и различаются в экспериментах с выведенными пучками и в коллайдерных экспериментах.

3.3.2. Метод измерения полного сечения на ускорителе с пересекающимися пучками по светимости пучков

Если известна светимость пучка , то число взаимодействий

N = ·σ_tot,

где

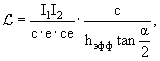
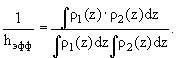
I₁, I₂ − токи в пучках 1 и 2; с − скорость света; α − угол между пучками; ρ₁(z), ρ₂(z) − плотности потоков в пучках 1 и 2.
Точность измерения невысока (~ 0.5%). Необходимо использовать 4π-геометрию вокруг точки пересечения, чтобы увеличить точность измерения h_эфф.

3.3.3. Измерение сечений рр-взаимодействий на встречных пучках с использованием Римских горшков

Измерения сечений с использованием оптической теоремы более точны, но в случае пересекающихся пучков требуется использовать детекторы, максимально приближающиеся к пучку, чтобы измерить dσ/dt при самых малых углах рассеяния. С этой целью используются детекторы, помещенные внутрь специальных цилиндров, получивших название "Римские горшки", т.к. впервые были использованы физиками, работающими в Риме. Поперечное сечение такого цилиндра, обозначенного RP, показано на рис. 23. Там же показано расположение Римских горшков относительно соударяющихся пучков протонов.

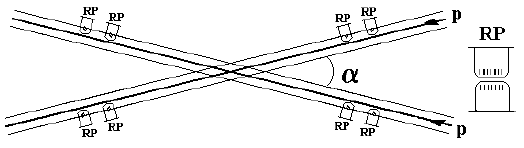
Рис. 23. Схема пересечения пучков протонов под углом a (RP − Roman Pots).

    Метод с использованием Римских горшков основан на одновременной регистрации упругого рассеяния N_el при низких t и числа неупругих взаимодействий N_inel.
    Поскольку Римские горшки расположены близко к траектории соударяющихся протонов, то с их помощью можно зарегистрировать протоны после упругого соударения. Такие протоны отклоняются от первоначального направления движения на очень малые углы. Детекторы, расположенные внутри Римских горшков, должны регистрировать протоны, движущиеся после столкновения под такими малыми углами.
    Количество упругих взаимодействий N_el фиксируется в зависимости от угла рассеяния протонов θ, т.е. в зависимости от t. Поэтому детекторы внутри Римских горшков должны иметь хорошее пространственное разрешение.
    Кроме этих устройств в экспериментальной установке должны присутствовать детекторы, позволяющие регистрировать количество неупругих взаимодействий N_inel.
    Этот способ измерения поперечных сечений коррелирует с предыдущим способом − измерением сечений по интегральной светимости , т.к.

·σ_tot= N_el + N_inel.

Оптическая теорема, которая связывает полное сечение с мнимой частью амплитуды упругого рассеяния вперед, приводит к следующим соотношениям:

Комбинируя эти соотношения, можно исключить машинную светимость и полное сечение в зависимости от измеряемых величин будет определяться по формуле

где ρ = Re ƒ(0)/Im ƒ(0) − отношение действительной части амплитуды упругого рассеяния вперед ƒ(0) к ее мнимой части. Это отношение ρ(√s) определяется независимо.

3.3.4. Метод измерения сечений в космических лучах

Во всех методах измерения сечений в космических лучах используется экспоненциальная зависимость:

N(x) = N₀ехр(σ·nх),

где N₀ − число частиц упавших на слой x, N(x) − число частиц, прошедших без взаимодействия слой х, σ − поперечное сечение взаимодействий, n − число слоев х.
Постановка эксперимента меняется в зависимости от энергии E₀ первичной частицы.

Е₀ < 10¹² эВ

Эксперименты выполняются с использованием калориметрических установок, располагающихся на горах. Среди частиц N₀, падающих на калориметрические устройства, могут присутствовать любые адроны, образующиеся в атмосфере Земли над экспериментальной установкой. В качестве мишеней используются поглотители, помещенные между детекторами частиц. Это могут быть графитовые, железные или свинцовые мишени. Таким образом, в этих экспериментах изучаются сечения взаимодействия адронов с различными атомными ядрами. В калориметрах фиксируется взаимодействие упавшего адрона с ядром мишени. Изучаются изменения числа таких взаимодействий с глубиной калориметра. Схема постановки эксперимента и ее результат показаны на рис. 24.

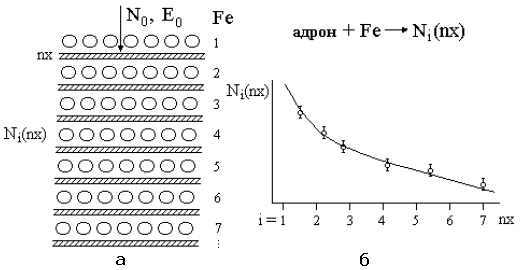
Рис. 24: Схема постановки эксперимента: а − калориметр для измерения поперечного сечения при энергии E₀ < 10¹² эВ; б − число частиц N_i(nx), зарегистрированных в калориметре под слоем (nх).

Экспоненциальная зависимость числа частиц, зарегистрированных под слоем (пж), позволяет определить поперечное сечение а адрон-ядерного взаимодействия.

Е₀ → 10¹⁶ эВ

На рис. 25 иллюстрируются процессы взаимодействия первичной частицы космического излучения в экспериментах для изучения поперечных сечений. Использование калориметров с площадью ~10×0 м , располагающихся на горах (на высоте более 5 км), позволяет измерить поперечные сечения при более высоких энергиях вплоть до 10¹⁶ эВ. В этом случае регистрируются частицы, прошедшие без взаимодействия через атмосферу Земли и провзаимодействовавшие в калориметре (рис. 25а). Отсутствие сигналов в детекторах, расположенных вокруг калориметра, свидетельствует о том, что первичная частица в атмосфере не провзаимодействовала.

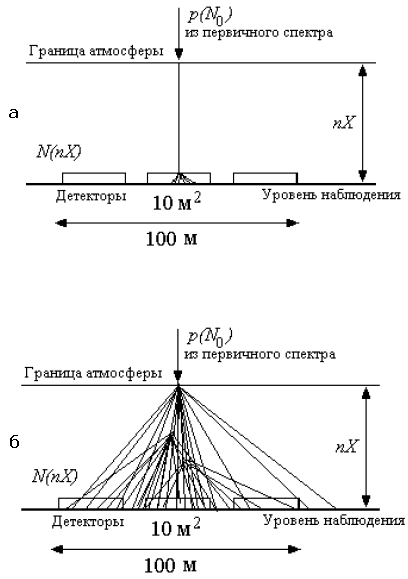
Рис. 25: Схема предполагаемых процессов взаимодействия первичных частиц космического излучения в атмосфере Земли: а − первичная частица, дошедшая до уровня наблюдения без взаимодействия, провзаимодействовала в калориметре; б − первичная частица провзаимодействовала в атмосфере Земли.

При переходе к еще более высоким энергиям калориметрические измерения становятся затруднительными и в качестве мишени используется атмосфера Земли. В этом случае первичные космические частицы (большинство из которых протоны), проходя через атмосферу Земли, генерируют ливни, которые регистрируются большим количеством детекторов, располагающихся на уровне наблюдения (рис. 256).
В обоих случаях помимо факта регистрации взаимодействия (в калориметре или в атмосфере Земли) требуется знание энергетического спектра первичного космического излучения.

E₀ > 10¹⁶ эВ

Для измерения сечений взаимодействий частиц с энергией E₀ > 10¹⁶ эВ используются данные по регистрации числа широких атмосферных ливней (ШАЛ) N_ШАЛ на глубине nХ. Для этой цели применяются установки, детекторы которых покрывают площади до 10 м и выше (рис. 26).

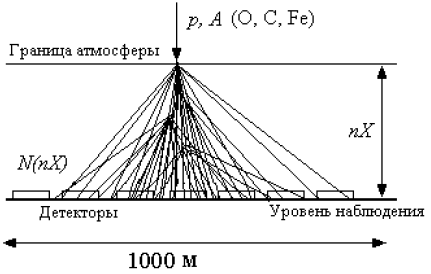
Рис. 26: Использование широких атмосферных ливней (ШАЛ) для измерения сечений частиц с энергией от 10¹⁰ до 10²⁰ эВ. N(nX) = N0(l − e^-σnx).

С помощью таких установок могут быть измерены сечения вплоть до энергий 10²⁰ эВ. В настоящее время проводятся эксперименты для уточнения спектра первичного космического излучения до столь высоких энергий. Измерение сечений при таких энергиях пока не выполнено.

Литература

THE EUROPEAN PHYSICAL JOURNAL C. Particles and Fields. Zietschrift fur Pliysik C. v.15, No.1-4, 2000. Springer.
Мурзин B.C., Сарычева Л.И. Множественные процессы при высоких энергиях. -М.: Атомиздат, 1974.
Мурзин B.C., Сарычева Л.И. Физика адронных процессов. -М.: Эиергоатомиздат, 1986.