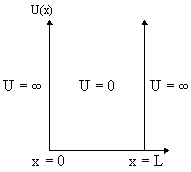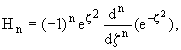|
Частица массы m находится в одномерной потенциальной яме бесконечной глубины (рис. 1). Потенциальная энергия U удовлетворяет следующим граничным условиям
U(x) = { |
0 0 < x < L |
(1) |
При таких граничных условиях частица находится внутри потенциальной ямы 0 < x < L и не может выйти за ее пределы, т.е.
|
(2) |
Условие нормировки
|
(3) |
Используя станционарное уравнение Шредингера для случая U = 0, получим
|
(4) |
или
|
(5) |
где
a2 = 2mE/ |
(6) |
Уравнение (5) описывает положение частицы внутри потенциальной ямы. Оно имеет решение
|
(7) |
представляющее собой суперпозицию двух волн,
распространяющихся в противоположных
направления вдоль оси x.
Постоянные A и B находятся из граничных
условий (2)
A + B = 0 при x = 0 т.е. B = -A. |
(8) |
Следовательно
|
(9) |
Условие ψ(L) = 0 дает
2ia sin aL = 0. |
(10) |
Отсюда
aL = n |
(11) |
Подставляя полученное значение a в соотношение (6), получим соотношение для энергии частицы в бесконечной прямоугольной яме
En = |
(12) |
Волновые функции (9) имеют вид
|
(13) |
Константу A можно получить из условия
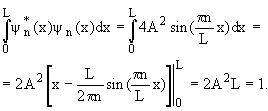
Нормированные волновые функции и собственные значения энергии для различных состояний приведены в табл. 1.
Таблица 1.
| n | Собственные функции |
Плотности вероятности |
Собственные значения энергии |
| 1 | i(2/L)1/2sin( |
(2/L)sin2( |
|
| 2 | i(2/L)1/2sin(2 |
(2/L)sin2(2 |
4 |
| 3 | i(2/L)1/2sin(3 |
(2/L)sin2(3 |
9 |
| n | i(2/L)1/2sin(n |
(2/L)sin2(n |
n2 |
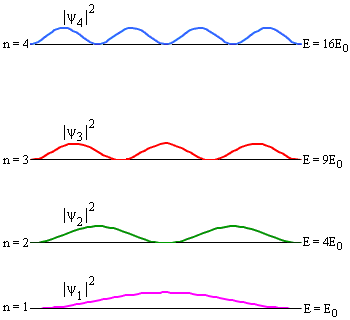
На рис. 2 показаны плотности вероятности
обнаружения частицы в различных квантовых
состояниях.
Таким образом, для бесконечной
одномерной потенциальной ямы имеем следующее.
- Энергия частицы принимает определенные дискретные значения. Обычно говорят, что частица находится в определенных энергетических состояниях.
- Частица может находиться в каком-то одном из множества энергетических состояний.
- Частица не может иметь энергию равную нулю.
- Каждому значению энергии En соответствует
собственная волновая функция
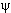 n, описывающая данное состояние.
n, описывающая данное состояние. - Для собственной функции
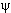 1(x)
вероятность обнаружить частицу в точке x = L/2
максимальна. Для состояния
1(x)
вероятность обнаружить частицу в точке x = L/2
максимальна. Для состояния 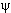 2(x) вероятность обнаружения частицы
в этой точке равна 0.
2(x) вероятность обнаружения частицы
в этой точке равна 0.
|
В случае гармонического осциллятора потенциальная энергия U имеет вид
U = kx2/2. |
(14) |
Станционарное уравнение Шредингера для гармонического осциллятора имеет вид
|
(15) |
Также как и в случае прямоугольной потенциальной ямы наблюдается дискретный спектр энергий состояний
En = (n + 1/2)h |
(16) |
где ![]() = (k/m)1/2.
Однако в отличие от прямоугольной ямы, спектр
энергий эквидистантный. Каждому энергетическому
состоянию соответствует волновая функция,
описываемая полиномом Эрмита Hn.
= (k/m)1/2.
Однако в отличие от прямоугольной ямы, спектр
энергий эквидистантный. Каждому энергетическому
состоянию соответствует волновая функция,
описываемая полиномом Эрмита Hn.
|
(17) |
|
(18) |
где a2 = 4![]() 2m
2m![]() /h, ζ= ax.
В табл. 2 приведены собственные значения
энергии En и нормированные собственные
функции гармонического осциллятора
/h, ζ= ax.
В табл. 2 приведены собственные значения
энергии En и нормированные собственные
функции гармонического осциллятора ![]() n
n
Таблица 2
| n | Собственные значения энергии En | Нормированные собственные
функции |
| 0 | E0 = h |
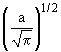 e-a2x2/2 e-a2x2/2 |
| 1 | E0 = 3h |
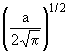 2axe-a2x2/2 2axe-a2x2/2 |
| 2 | E0 = 5h |
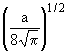 (4a2x2 - 2)e-a2x2/2 (4a2x2 - 2)e-a2x2/2 |
| 3 | E0 = 7h |
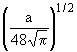 (8a3x3 - 12ax)e-a2x2/2 (8a3x3 - 12ax)e-a2x2/2 |
| n | En = (n + 1/2)h |
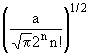 Hn(ax)e-a2x2/2 Hn(ax)e-a2x2/2 |
|
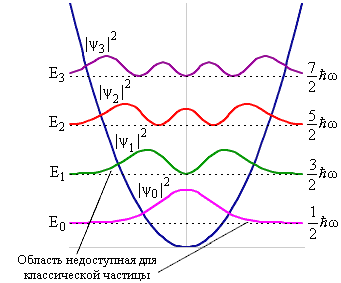
На рис. 3 показана плотность распределения
волновой функции гармонического осциллятора.
Классический осциллятор не может
выйти за пределы значений x, в которых
потенциальная энергия равна энергии En для
данного значения квантового числа n. В квантовом
случае ситуация другая - существует отличная от
нуля вероятность обнаружить частицу за
пределами потенциальной ямы, т.е. частица может
проникать на небольшое расстояние за стенку
барьера.
17.01.14