< Previous | Contents | Next >
Повышенная трудоемкость является существенным недостатком неявных схем, особенно если речь идет о таких больших системах уравнений, как в слу- чае задачи звездного горения. Даже для современных вычислительных мощ- ностей эффективная реализация такого алгоритма представляет определенную сложность. В связи с этим одним из актуальных направлений исследования в данной области является поиск явных схем, применимых к специфическим жестким задачам. Такая альтернатива неявным методам существенно облегчи- ла бы расчет ядерных трансмутаций. Явные методы для решения сверхжестких задач химической кинетики представлены в работах [17] и [20], а в исследовании
[18] указывается на возможность применения некоторых таких схем к задачам звездного горения.
При построении этих методов используется специфика самой задачи. Общая особенность уравнений химических и ядерных (8) превращений заключается в том, что все процессы, которым соответствуют элементы суммы в правой части,
делятся на нарабатывающие и расходующие - первые имеют положительные значения, вторые отрицательные. Тогда для i-й компоненты системы можно записать:
dyi
![]()
dt
i
i
i
i
= f (t) = q (t) − p (t)y (t) (12)
3.3.1. Специальная явная схема
Метод, описанный в работе [19, 20], применяет возможность разделения по- ложительных qi(t) и отрицательных pi(t)yi(t) вкладов следующим образом:
yi,n+1 =
y i,n + hqi(y˜)[1 + 1hqj(y˜)] 1 + hpi(y˜) + 1h2p2(y˜)
y˜ =
(yn+1 + yn) (13)
![]()
1
2
2 ,
2 j
Представленная система уравнений выражает искомое значение yi,n+1 неяв- но. Решая ее двумя итерациями, можно достигнуть второго порядка точности, получив таким образом явную схему. В дополнение к этому авторы рекомен- дуют пользоваться методом геометрически-адаптивного выбора шага. Идея за- ключается в переходе от аргумента времени к величине длины дуги решения l:
j=0
j
dl2 = N du2, где N - число компонент системы, uj = yj/ yj, u0 = t/T , где
T - полное время эволюции системы. Такая параметризация позволяет неявно измельчать шаг в областях повышенной крутизны дуги решения.
В рамках настоящей работы специальная явная схема была реализована на языке Fortran и встроена в систему MESA. Испытания с простейшей схемой из двух изотопов дали удовлетворительные результаты, сошедшиеся с резуль- татами штатного интегратора MESA и проверенные аналитически. Однако на более сложной сети из 31 изотопа явный метод давал концентрации (рис. 18a), на порядки отличающиеся от результатов эталонной схемы (рис. 18b). Причина расхождений заключается в неконсервативности явной схемы - между шагами возникает дисбаланс концентраций, непринципиальный для расчета химиче- ских реакций на коротких временах, но существенно сказывающийся на мо- делировании процессов нуклеосинтеза на астрофизическом масштабе времени.


Концентрация H1
Концентрация H1
0.8 0.8
0.6 0.6
0.4 0.4
0.2 0.2
0
0 ⋅ 100 2 ⋅ 106 4 ⋅ 106 6 ⋅ 106 8 ⋅ 106 10 ⋅ 106
40 ⋅ 10-12
Концентрация Si28
30 ⋅ 10-12
20 ⋅ 10-12
10 ⋅ 10-12
0 ⋅ 100
0 ⋅ 100 2 ⋅ 106 4 ⋅ 106 6 ⋅ 106 8 ⋅ 106 10 ⋅ 106
Время, с
(a)
0
0 ⋅ 100 2 ⋅ 106 4 ⋅ 106 6 ⋅ 106 8 ⋅ 106 10 ⋅ 106

Концентрация Si28
30
20
10
0
0 ⋅ 100 2 ⋅ 106 4 ⋅ 106 6 ⋅ 106 8 ⋅ 106 10 ⋅ 106
Время, с
(b)
Рис. 18. Сравнение результатов расчета системы из 31 изотопа специальной схемой (a) и неявным методом MESA (b) для изотопов 1H и 28Si.
log Относительная концентрация
0
e
danc
abun tive
Rela log
![]()
-5
-10
-15
-20
-25
-30
-14 -12 -10 -8 -6 -4 -2 0
s
log t,
![]()
log t/секунда
1H
![]()
![]()
![]()
4He 12C
![]()
14N
![]()
16O
![]()
20Ne
![]()
![]()
24Mg MESA
QSSM
Из-за этой особенности метод, по всей видимости, неприменим к поставленной задаче.
3.3.2. Метод QSS
Другой явный метод, предложенный в работе [17], был исследован в работе
[18] на предмет применимости к задаче термоядерного горения. При построении схемы пользуются тем, что в приближении постоянного или линейного вида функций qi(t) и pi(t) можно получить аналитические решения уравнения (12). Анализ этих решений позволил построить два выражения:
![]()
yp = y0
+ ∆t(q0 − p0y0) 1 + α(∆tp0)∆tp0
, yc
= y0
+ ∆t(q˜− p¯y0)
![]()
1 + α(∆tp¯)∆tp¯
(14)
Величины yp и yc носят название предиктора и корректора. В представленных
2
выше выражениях p¯ = 1(p0 + pp), p˜ = α(∆tp¯)qp + (1 − α(∆tp¯))q0, а функция
α(r) имеет следующий вид:
α(r) =
1 − (1 − e−r)/r (15)
![]()
1 − e−r
Предиктор вычисляется в качестве оценочного значения, корректор уточ- няет оценку. Разница предиктора и корректора позволяет оценить ошибку за шаг.
Аналогично специальной явной схеме, в ходе данной работы метод QSS был реализован на базе MESA. Проведено сравнение результатов, полученных мето- дом QSS и схемой MESA, описанной выше. Расчеты проводились на стандарт- ной ядерной системе, использующейся в MESA для моделирования процесса
<горячего> CNO-цикла (взрывная форма обычного CNO-цикла, протекающая
∼
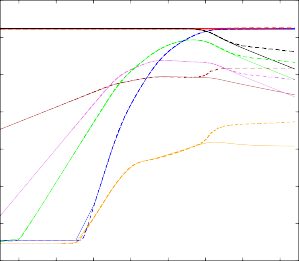
в экстремальных условиях, например, при взрыве сверхновой). Результаты рас- четов представлены на рис. 19. Начиная с 10−4 с наблюдаются расхождения между решениями QSS и MESA, вероятно, объясняющиеся похожей проблемой
дисбаланса концентраций схемы QSS. Однако следует отметить, что на данный момент мы не успели внедрить механизм подстройки шага в алгоритм QSS. Алгоритм еще может быть значительно оптимизирован.
Преимуществом метода QSS является большая простота в сравнении с инте- гратором MESA и специальной явной схемой. В настоящее время продолжается работа по его программной реализации.