< Previous | Contents | Next >
Общепринятым способом решения жестких задач является применение неяв- ных методов, которые, в отличие от явных, обладают большей устойчивостью. Однако в неявные разностные схемы неизвестная величина, то есть значение решения на следующем шаге, входит не единожды, поэтому для ее нахождения
приходится решать алгебраическое уравнение. Тем самым на один шаг инте- грирования неявный метод затрачивает значительно большее число операций, чем требовалось бы явному, если он применим к рассматриваемой задаче.
3.2.1. Неявный метод Эйлера
Библиотека симуляции процессов нуклеосинтеза SkyNet, представленная в разделе 2 и применявшаяся нами для моделирования r-процесса с измененны- ми скоростями некоторых реакций, использует неявную модификацию метода Эйлера для расчета эволюции концентраций изотопов. Неявный метод Эйлера задает значение решения в следующем узле yn+1 при помощи уравнения
yn+1 = yn + hf (yn+1), (10)
где h - длина шага по времени. Как видно, неизвестная величина yn+1 в общем случае не может быть выражена явно. Разрешение этого уравнения относитель- но yn+1 процедурой Ньютона требует вычисления якобиана, что значительно повышает трудоемкость расчета. Кроме того существует опасность, что итера- ционный процесс не сойдется к допустимой величине ошибки за конечное время, что существенно снижает надежность метода. На практике обычно ограничи- ваются конечным числом итераций, а требуемая точность достигается путем параллельного расчета на двух разных сетках интегрирования - тогда ошибку оценить по разности решений с различным шагом.
При использовании конечного числа итераций неявный метод Эйлера фак- тически превращается в явную схему, которую можно применять для решения жестких систем уравнений. Для одной итерации метода Ньютона, которой ча- сто и ограничиваются, формула для расчета решения на следующем шаге имеет вид
(I/h − J ) · ∆ = f (yn), (11)
k
где I - единичная матрица, J - якобиан правых частей, Ji = ∂fi/∂yk, ∆ =
−
yn+1 yn - искомое изменение вектора концентраций.
Основным недостатком неявного метода Эйлера является его большая тру- доемкость, сохраняющаяся даже при выборе конечного числа итераций проце- дуры Ньютона. Большое число требуемых операций обусловлено необходимо- стью вычисления якобиана J и последующей работы с ним. Расчет односекунд- ного r-процесса на персональном компьютере посредством библиотеки SkyNet занимал около 20 минут. Для крупномасштабных симуляций астрофизических процессов такие времена получения решения неприемлемы.
3.2.2. Влияние шага интегрирования
Очевидно, что величина временного шага h существенно влияет на резуль- тат моделирования. Для оценки этого влияния расчет r-процесса неявным ме- тодом Эйлера при помощи библиотеки SkyNet был проведен нами на различ- ных сетках интегрирования, величина шага модифицировалась искусственно.


(a) A = 56 (b) A = 208
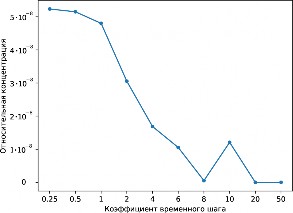
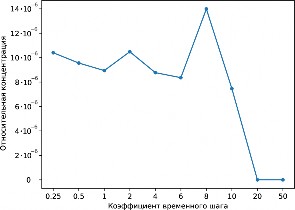
Рис. 15. Влияние размера шага на конечные концентрации изотопов для двух массовых чисел A. Расчет при помощи библиотеки SkyNet.
Результаты для изотопов с массовыми числами 56 и 208 приведены на рис. 15. Как видно, вариации шага в пределах порядка могут привести к исчезновению изотопов с малыми концентрациями, представляющих интерес при изучении распространенности ядер.
Для получения оптимальной густоты сетки интегрирования пользуются все- возможными реализациями метода адаптивного выбора шага, сводящегося к оценке величины полученной на текущем шаге ошибки и принятия программой решения о необходимости уменьшить шаг для повышения точности расчета или увеличить его для сокращения времени симуляции.
3.2.3. Численный метод системы MESA
Продвинутые неявные методы обладают большей точностью и производи- тельностью. В библиотеке астрофизического моделирования MESA в качестве штатной схемы интегрирования используется неявный метод переменного по- рядка точности [22, 23], являющийся развитием метода Эйлера. Это точная и эффективная схема, использующаяся в данной работе в качестве эталонной.
−
Полный шаг интегрирования H между состояниями yn и yn+1 разбивается на несколько микрошагов h = H/m, разделяющих промежуточные состояния yk (k = 1, m). Вводится вспомогательная переменная ∆k = yk+1 yk, изменение концентраций между шагами. Для нее выполняется алгоритм:
∆0 = (I − hJ )−1hf (yn)
k = 1, m − 1 : yk = yk−1 + ∆k−1, ∆k = ∆k−1 + 2(I − hJ )−1[hf (yk) − ∆k−1]
ym = ym−1 + ∆m−1, ∆m = (I − hJ )−1[hf (ym) − ∆m−1]
yn+1 = ym + ∆m
Для оценки точности эта последовательность действий выполняется на каж- дом шаге как минимум два раза с разными значениями m, то есть с разной точ- ностью. Ошибка определяется как разность результатов двух прогонок. Значе- ние ошибки используется в методе адаптивного шага: если ошибка превышает
5
log dt, s
0
-5
-10
-15
-20
-20 -15 -10 -5 0 5 10
log t, s
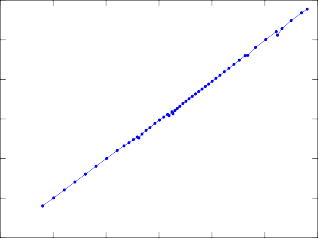
желаемую, шаг уменьшается, а при удовлетворительной ошибке увеличивается. Пример поведения шага при моделировании процесса горения звездного веще- ства описанной схемой MESA приведен на рис. 16. В целях контроля точности в алгоритме также варьируются значения m.
Скорость расчета модельных ядерных систем, описывающих конкретные процессы астрофизического нуклеосинтеза и включающих лишь десятки изо- топов, при помощи данного неявного метода очень высока. Однако симуляция таких глобальных явлений, как r-процесс, требует единовременного отслежи- вания изменения концентраций тысяч изотопов. При этом требуется вычислять якобиан огромной системы уравнений и совершать с ним матричные операции, что многократно повышает трудоемкость метода. Тем самым метод MESA, бу- дучи чрезвычайно точным и эффективным на малых системах ядерных реак- ций, не подходит для расчета r-процесса.
3.2.4. Якобиан системы уравнений
∂y
Остановимся отдельно на структуре якобиана J . Возвращаясь к использо- ванному выше примеру реакции 12C(α, γ)16O, выпишем обусловленные ею эле- менты якобиана Jik = ∂fi :
k
J (4He, 4He) = −λy(12C) + ..., J (12C, 12C) = −λy(4He) + ...,
J (4He, 12C) = −λy(4He) + ..., J (16O, 4He) = +λy(12C) + ...,
J (12He, 4He) = −λy(12C) + ..., J (16O, 12C) = +λy(4He) + ...
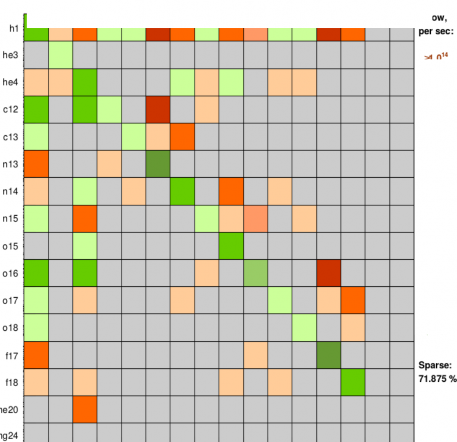
Если i-ый изотоп не участвует ни в одной реакции, задействующей k-ый, то соответствующий элемент якобиана Jik будет равен нулю. Полный якобиан будет в общем случае несимметричным, потому что скорости прямых и обрат- ных реакций могут значительно различаться, а также сильно разреженным, так как для многих пар изотопов реакции либо отсутствуют, либо дают малый
1H 3He 4He 12C 13C 13N 14N 15N 15O 16O 17O 18O 17F 18F 20Ne 24Mg
1H
3He 4He 12C
13C
13N
14N
15N
15O
16O
17O
18O
17F
18F
20Ne
24Mg
≥1014
≥1010
≥106
≥102
>0
=0
≥-102
≥-106
≥-10
≥-101
<-101
1
вклад. Пример модельного якобиана, полученного в ходе исследования числен- ных схем, приведен на рис. 17. В соответствующем реальной астрофизической системе якобиане число элементов достигает сотен тысяч, что позволяет пред- ставить трудоемкость такого расчета.