< Previous | Contents | Next >
При расчете сечений ядерных реакций необходимо знать массы исходных и конечных ядер, так как эти величины используются при вычислении энерге- тических порогов процессов и приведенной массы взаимодействующих частиц. Характеристики стабильных и долгоживущих изотопов, которые могут быть получены экспериментально, определяются с хорошей точностью и могут быть найдены в банках ядерных данных, таких как AME [2, 14]. Для экзотических же ядер получение точных масс представляет большую трудность. Существующие модели не могут быть проверены экспериментально и, как выясняется, суще- ственно расходятся между собой. Предсказание масс экзотических r-нуклидов в области нейтроноизбыточных изотопов, для которых практически отсутству- ют экспериментальные данные, является актуальной проблемой современной физики.
2.3.1. Модель FRDM
Приближение жидкой капли - наиболее простое представление о ядре, ко- торое может быть расширено путем учета микроскопических структурных эф- фектов. Примером такого расширения является модель FRDM [15], в которой для вычисление макроскопического вклада в энергию используется продвину- тое многокомпонентное приближение жидкой капли, а оболочечные эффекты учитываются при помощи метода усреднений Струтинского [16].
В 1995 году были опубликованы теоретические массы и параметры дефор- мации, рассчитанные при помощи модели FRDM1992, для 8979 изотопов вплоть до массового числа 339. Всего существует несколько версий данной микро- макроскопической модели, каждая из которых уточняет предыдущую. В про- грамме TALYS массы, полученные с помощью FRDM2012, представлены в ка- честве одной из опций теоретической массовой модели. Массы FRDM1992 ис- пользуются в программе NON-SMOKER по умолчанию, они же представлены в библиотеке скоростей астрофизических реакций REACLIB в качестве реко- мендованных.
2.3.2. Метод Хартри-Фока-Боголюбова
Построение теоретических массовых моделей, явно учитывающих микро- скопическую структуру, затруднено тем фактом, что ядро представляет из себя сложную квантовомеханическую систему многих тел. Для детального описания подобных систем в квантовой химии, ядерной и атомной физике часто приме- няется метод самосогласованного поля. Идея заключается в построении эффек- тивного потенциала силы, действующей на одну частицу со стороны всей си- стемы и складывающейся из каждого парного взаимодействия. Метод Хартри-
Фока-Боголюбова (HFB) является широко используемой вариацией этого мето- да, учитывающей парные корреляции частиц.
На базе метода Хартри-Фока-Боголюбова строятся многочисленные моде- ли, использующие различный вид потенциала самосогласованного поля. В про- грамме TALYS они представлены моделями HFB с потенциалами Скирма и Гоньи. Данные метода HFB с потенциалом Скирма используются в программе по умолчанию, сечения, показанные в разделе 2.2 на рис. 8, рассчитаны именно с этой массовой моделью.
2.3.3. Погрешность предсказания масс нейтроноизбыточных ядер

Skyrme-HFB Gogny-HFB
Разница с результатом модели FRDM2012, МэВ
4
3
2
1
0
-1
-2
140 150 160 170 180 190 200
Массовое число
На рис. 11 представлена разность масс изотопов тербия, рассчитанных при помощи метода Хартри-Фока-Боголюбова с потенциалами Скирма и Гоньи, и массы, полученной в макро-микроскопическом приближении FRDM. Как вид- но, для самых тяжелых нейтроноизбыточных ядер погрешность превышает 4 МэВ. Это согласуется с данными обзора [3], согласно которому разница между массами, полученными различными современными ядерными моделями, может достигать 10 МэВ.
2.3.4. Результаты расчетов
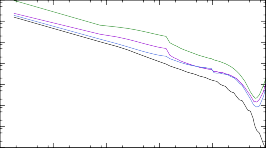
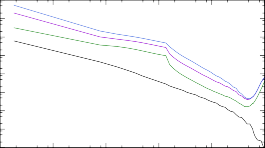
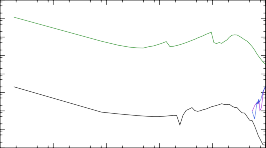
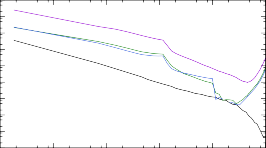
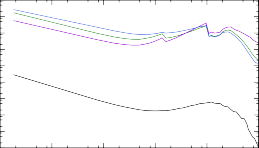
С помощью TALYS для трех теоретических массовых моделей были вы- числены сечения реакции нейтронного захвата на ядрах 187÷193Tb. В качестве модели ядерных уровней оставлена CTM, использующаяся в TALYS по умолча- нию. Результаты расчета представлены на рис. 12. Как в случае рис. 8, наблю- дается серьезное расхождение с результатами расчета посредством программы NON-SMOKER для самых тяжелых ядер. Так же становится ясно, что реакция 191Tb(n, γ)192Tb в рамках моделей, основанных на методе HFB, обладает вы-
100
10-1
Сечение, бн
10-2
10-3
10-4
10-5
10-6
10-7
187Tb + n → 188Tb
101
100
Сечение, бн
10-1
10-2
10-3
10-4
10-5
10-6
10-7
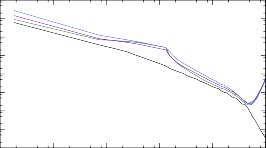
188Tb + n → 189Tb
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
100
10-1
Сечение, бн
10-2
10-3
10-4
10-5
10-6
10-7
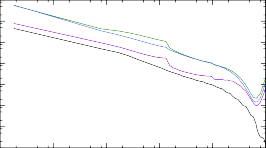
189Tb + n → 190Tb
101
100
Сечение, бн
10-1
10-2
10-3
10-4
10-5
10-6
10-7
190Tb + n → 191Tb
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
10-1
10-2
Сечение, бн
10-3
10-4
10-5
10-6
10-7
10-8
10-9
191Tb + n → 192Tb
100
10-1
Сечение, бн
10-2
10-3
10-4
10-5
10-6
10-7
10-8
10-9
192Tb + n → 193Tb
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
10-1
10-2
Сечение, бн
10-3
10-4
10-5
10-6
10-7
10-8
10-9
10-10
193Tb + n → 194Tb
![]()
NON-SMOKER FRDM1992 TALYS FRDM2012
![]()
![]()
TALYS Skyrme-HFB TALYS Gogny-HFB
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
Рис. 12. Сечения реакций (n, γ) на ядрах 187÷193Tb, рассчитанные при помощи программ NON-SMOKER и TALYS для трех массовых моделей: Хартри-Фока-Боголюбова с потенци- алами Скирма и Гоньи и жидкокапельной модели FRDM.
20.0%
15.0%
10.0%
5.0%
0.0%
-5.0%
187Tb + n → 188Tb
30.0%
25.0%
20.0%
15.0%
10.0%
5.0%
0.0%
-5.0%
188Tb + n → 189Tb
160 180 200 220 240
Массовое число
160 180 200 220 240
Массовое число
25.0%
20.0%
15.0%
10.0%
5.0%
0.0%
-5.0%
189Tb + n → 190Tb
16.0%
14.0%
12.0%
10.0%
8.0%
6.0%
4.0%
2.0%
0.0%
-2.0%
190Tb + n → 191Tb
160 180 200 220 240
Массовое число
160 180 200 220 240
Массовое число
20.0%
15.0%
10.0%
5.0%
0.0%
-5.0%
-10.0%
-15.0%
-20.0%
-25.0%
191Tb + n → 192Tb
3.0%
2.0%
1.0%
0.0%
-1.0%
-2.0%
-3.0%
-4.0%
-5.0%
192Tb + n → 193Tb
160 180 200 220 240
Массовое число
160 180 200 220 240
Массовое число
8.0%
6.0%
4.0%
2.0%
0.0%
-2.0%
193Tb + n → 194Tb
![]()
TALYS FRDM2012
![]()
![]()
TALYS Skyrme-HFB TALYS Gogny-HFB
-4.0%
160 180 200 220 240
Массовое число
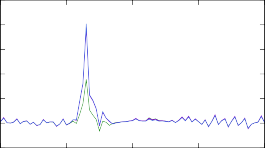
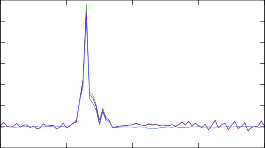
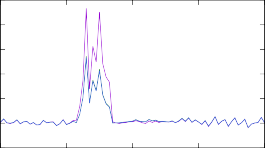
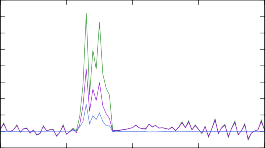
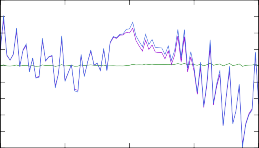
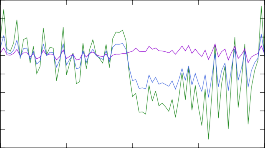
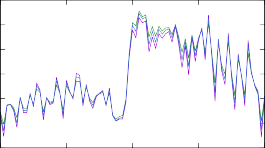
Рис. 13. Изменение концентраций в результирующем массовом распределении модели r- процесса после изменения скоростей реакций при помощи различных массовых моделей. Изменениям подвергались скорости реакции (n, γ) на изотопах тербия 187÷193Tb.
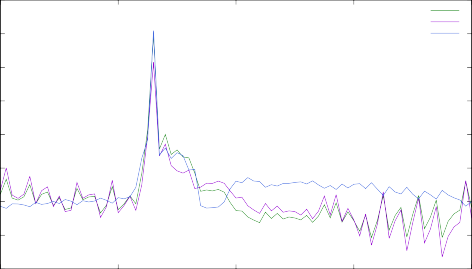
TALYS FRDM2012
TALYS Skyrme-HFB TALYS Gogny-HFB
50%
40%
30%
20%
10%
0%
-10%
-20%
160 180 200 220 240
Массовое число
Рис. 14. Суммарное изменение концентраций при изменении скоростей нейтронного захвата с использованием различных массовых моделей для изотопов 187÷193Tb.
соким энергетическим порогом, что и является причиной отсутствия сечений низкоэнергетической реакции.
Обращает на себя внимание сильное различие низкоэнергетических сечений, полученных с помощью различных массовых моделей TALYS. Это показыва- ет роль массовых моделей, на основе которых рассчитываются такие важные параметры реакции, как энергетический порог.
Результаты моделирования r-процесса с рассчитанными таким образом ско- ростями реакций представлены на рис. 13. Изменение результирующих массо- вых распределений такое же существенное, как и в случае с моделями уровней, относительные отклонения достигают 30 %. Наименее предсказуемая картина наблюдается для трех самых тяжелых ядер, сечения реакций на которых малы и, судя по рис. 12, кардинально расходятся в различных моделях.
Результаты расчета r-процесса с одновременным изменением скоростей ре- акции нейтронного захвата на всех изотопах 187÷193Tb по описанным выше
теоретическим массовым моделям представлены на рис. 14. Как видно, сте- пень неопределенности для массовых моделей сопоставима с неопределенно- стью, связанной с выбором модели уровней.