< Previous | Contents | Next >
Вычисление сечений ядерных реакций требует учета возбужденных состоя- ний начального и конечного ядер. При энергиях возбуждения выше нескольких МэВ количество дискретных уровней на единицу энергии настолько велико, что они практически сливаются. Для расчета сечений целесообразно рассматривать не отдельные состояния, а величину плотности ядерных уровней ρ(Ex, J, Π) с энергией возбуждения Ex, моментом J и четностью Π. Учет момента и четности необходим для проверки законов сохранения.
Величины плотностей уровней определяют исходя из различных теорети- ческих моделей, среди которых выделяются “эффективные”, неявно учитыва- ющие сложные микроскопические и коллективные эффекты в ядре на основе более простых представлений. Большинство из них основываются на простом и удобном приближении Ферми-газа. В программе для расчета сечений ядерных реакций TALYS представлены три подобные модели.
2.2.1. Приближение Ферми-газа
![]()
ρF (Ex) =
√π
![]()
![]()
x
12a1/4E5/4
e2√aEx, (4)
где Ex - энергия возбуждения, a - параметр, связанный с гиромагнитными отношениями нуклонов, на практике выступающий в роли калибровочного па- раметра.
Чтобы распределение плотностей включало момент и четность, требуется умножить ρF (Ex) на их распределения - нормальное по J и равномерное по Π. Кроме того, для учета эффекта спаривания в правых частях выражения (4) от
−
переменной энергии возбуждения Ex переходят к величине U = Ex ∆, где ∆ - параметр, фактически соответствующий энергии спаривания нуклонов в ядре. Таким образом вносится поправка на необходимость разрыва пары для перево- да ядра в следующее возбужденное состояние. Тогда формула распределения плотности ядерных уровней принимает вид
![]()
![]()
ρF (Ex, J, Π) =
12a1/4U 5/4 e
· 2σ2√2πσ2 exp
−
, (5)
2
√π 2√aU
![]()
2J + 1
![]()
J (J + 1) 1
2σ2
где σ2 - величина, характеризующая ширину распределения моментов ядерных состояний.
Переменные a, σ2 и ∆ играют роль калибровочных параметров, выбор кото- рых зависит от модели и часто основывается на нестрогих полуэмпирических представлениях. Параметр a при этом является определяющим, а ∆ обычно сводится к энергии спаривания нуклонов. В программе TALYS a рассчитыва- ется на основе данных из библиотеки ядерных параметров RIPL [10].
Рассмотрим модификации модели Ферми-газа для плотности ядерных уров- ней, представленные в TALYS и применявшиеся в данной работе.
2.2.2. Модель константной температуры
В модели Ферми-газа частицы считаются невзаимодействующими друг с другом. Это приближение хорошо описывает сильно возбужденное ядро, в ко- тором энергиями парных взаимодействий нуклонов можно пренебречь, одна- ко на низких уровнях модель не работает. Модель константной температуры (CTM), предложенная в [11], представляет собой естественное решение этой проблемы: вводится величина EM минимальной энергии возбуждения, при ко- торой применима модель Ферми-газа. Для более низких энергий используется подтвержденное для низколежащих уровней выражение
1
ρT (Ex) = T
exp Ex − E0 , (6)
![]()
T
где T и E0 - параметры, T носит название ядерной температуры. Тем самым выражение для плотности уровней в модели константной температуры имеет следующий вид:
ρ (E
, J, Π) = ρF (Ex, J, Π), если Ex ≥ EM
(7)
CTM x
1
2 R(Ex, J )ρT (Ex),
если Ex
≤ EM ,
где R(Ex, J ) - гауссово распределение момента.
Параметры E0, EM и T связаны между собой и рассчитываются по полуэм- пирическим формулам с учетом условия сшивки функции плотности уровней. Поправка сил спаривания ∆ для ядра с массовым числом A в модели констант-
ной температуры приближается выражением
12
∆CT M = χ√A
, χ =
0 для нечетно-нечетных
1 для четно-нечетных
2.2.3. Модель BFM
В модели BFM [12] (Back-shifted Fermi-gas model) общий вид зависимости (5), а учет парных взаимодействий нуклонов осуществляется за счет параметра ∆. Он рассчитывается следующим образом:
12
∆BFM = χ√A
+ δ, χ =
−1 для нечетно-нечетных
0 для нечетно-четных
1 для четно-четных,
где δ является калибровочной поправкой, наравне с a и σ2.
2.2.4. Обобщенная модель сверхтекучей жидкости
Как и CTM, обобщенная модель сверхтекучей жидкости (GSM) разделяет случаи низких и высоких энергий возбуждения. Учет парных корреляций про- исходит по аналогии с микроскопической теорией сверхпроводимости Бардина- Купера-Шриффера, основывающейся на понятии куперовской пары - двух связанных электронов с противоположными спинами и скоростями. При помо- щи теории БКШ были выработаны поправки к параметрами формулы (5), что позволило создать цельную теоретическую модель плотностей ядерных уров- ней. Подробное феноменологическое описание GSM представлено в [13].
2.2.5. Результаты расчетов
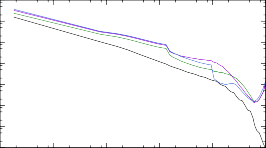
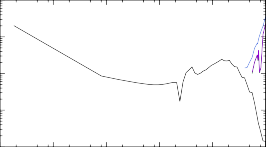
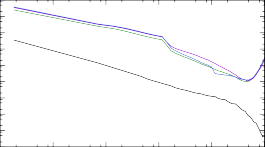
При помощи программы TALYS сечения и скорости протекания реакции нейтронного захвата на ядрах 187÷193Tb были рассчитаны с использованием мо- делей CTM, BFM и GSM. Результаты расчета сечений представлены на рис. 8 вместе с сечениями, полученными при помощи программы NON-SMOKER, ис- пользовавшейся при построении библиотеки астрофизических скоростей реак- ций REACLIB. Обращает на себя внимание существенное расхождение сечений TALYS и NON-SMOKER, растущее с набором массы.
Кроме того, видно качественное расхождение: сечения TALYS показывают рост вблизи 10 МэВ, в то время как сечения NON-SMOKER убывают. Это обу- словлено особенностями программы NON-SMOKER, разработанной специально для расчета сечений астрофизических реакций, идущих через механизм состав- ного ядра. Действительно, при температуре среды 1.2 ГК средняя кинетиче- ская энергия нейтронов составляет порядка 100 кэВ, в чем можно убедиться по рис. 3, - при таких энергиях не имеет смысла учитывать прямой механизм
100
10-1
Сечение, бн
10-2
10-3
10-4
10-5
10-6
10-7
187Tb + n → 188Tb
101
100
Сечение, бн
10-1
10-2
10-3
10-4
10-5
10-6
10-7
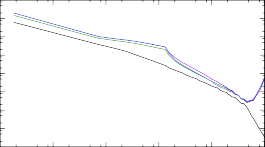
188Tb + n → 189Tb
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
100
10-1
Сечение, бн
10-2
10-3
10-4
10-5
10-6
10-7
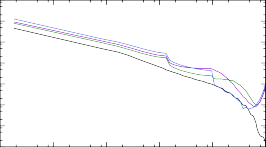
189Tb + n → 190Tb
101
100
Сечение, бн
10-1
10-2
10-3
10-4
10-5
10-6
10-7
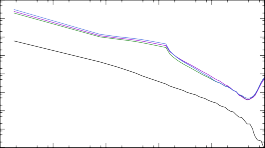
190Tb + n → 191Tb
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
10-5
Сечение, бн
10-6
10-7
10-8
10-9
191Tb + n → 192Tb
100
10-1
Сечение, бн
10-2
10-3
10-4
10-5
10-6
10-7
10-8
10-9
192Tb + n → 193Tb
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
10-1
10-2
Сечение, бн
10-3
10-4
10-5
10-6
10-7
10-8
10-9
10-10
193Tb + n → 194Tb
![]()
NON-SMOKER TALYS CTM
![]()
![]()
TALYS BFM TALYS GSM
10-4 10-3 10-2 10-1 100 101
Энергия нейтрона, МэВ
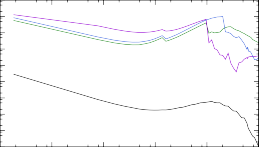
Рис. 8. Сечения реакций (n, γ) на изотопах тербия 187÷193Tb, расчитанные при помощи NON-SMOKER и TALYS с тремя вариациями модели Ферми-газа.
15.0%
10.0%
5.0%
0.0%
-5.0%
187Tb + n → 188Tb
30.0%
25.0%
20.0%
15.0%
10.0%
5.0%
0.0%
-5.0%
188Tb + n → 189Tb
160 180 200 220 240
Массовое число
160 180 200 220 240
Массовое число
25.0%
20.0%
15.0%
10.0%
5.0%
0.0%
-5.0%
189Tb + n → 190Tb
8.0%
7.0%
6.0%
5.0%
4.0%
3.0%
2.0%
1.0%
0.0%
-1.0%
190Tb + n → 191Tb
160 180 200 220 240
Массовое число
160 180 200 220 240
Массовое число
15.0%
10.0%
5.0%
0.0%
-5.0%
-10.0%
-15.0%
-20.0%
-25.0%
191Tb + n → 192Tb
1.5%
1.0%
0.5%
0.0%
-0.5%
-1.0%
192Tb + n → 193Tb
160 180 200 220 240
Массовое число
160 180 200 220 240
Массовое число
8.0%
6.0%
4.0%
2.0%
0.0%
-2.0%
193Tb + n → 194Tb
![]()
![]()
![]()
TALYS CTM TALYS BFM TALYS GSM
-4.0%
160 180 200 220 240
Массовое число
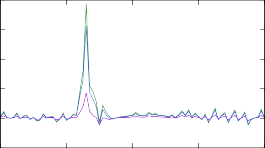
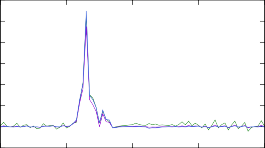
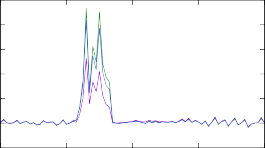
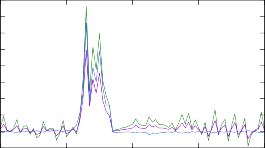
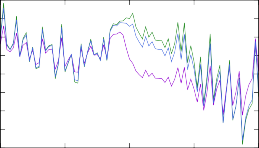
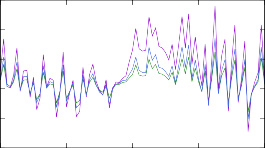
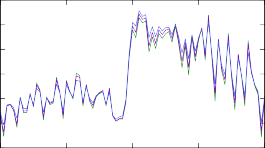
Рис. 9. Изменение концентраций в результирующем массовом распределении модели r- процесса после вычисления скоростей реакций при помощи различных моделей ядерных уровней. Изменениям подвергались скорости реакции (n, γ) на изотопах тербия 187÷193Tb.
TALYS CTM TALYS BFM TALYS GSM
50%
40%
30%
20%
10%
0%
-10%
-20%
160 180 200 220 240
Массовое число
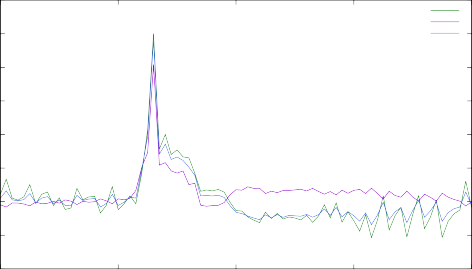
Рис. 10. Суммарное изменение концентраций при изменении скоростей нейтронного захвата с использованием различных моделей уровней для изотопов 187÷193Tb.
или предравновесные реакции. TALYS же является универсальной программой, поэтому рост сечения оправдан учетом механизма предравновесных реакций. С другой стороны, при более высоких температурах распределение имеет высоко- энергетический “хвост”, и для ряда реакций вклад предравновесного процесса вполне может оказаться заметным.
Также на рис. 8 для изотопа 191Tb на низких энергиях отсутствуют сечения всех моделей TALYS. Эта особенность обусловлена тем, что массовая модель, используемая TALYS по умолчанию, устанавливает высокий порог для данной реакции, из-за чего область ненулевых сечений обрезается. Подробно массовые модели будут обсуждены в разделе 2.3.
Для тех же ядер 187÷193Tb помимо сечений были рассчитаны скорости ней-
тронного захвата при температуре среды 1.2 ГК с использованием каждой из трех описанных выше вариаций модели Ферми-газа. Для каждой полученной скорости была проведена симуляция звездного r-процесса согласно модели, опи- санной в разделе 2.1. На рис. 9 показаны степени отклонения концентраций, вычисленных с модифицированными скоростями, от результатов первоначаль- ного расчета со стандартными скоростями из библиотеки REACLIB. Как видно, для самых легких из рассмотренных изотопов отклонения представляют собой всплески вплоть до 30% массовых числах, соответствующих рассматриваемым
реакциям, с сохранением общего фона. Для реакций на изотопах 191÷193Tb ре-
зультаты наглядно показывают, что изменение модели расчета одной единствен- ной реакции способно существенно изменить распределение концентраций, при- чем достаточно непредсказуемо.
На рис. 10 представлены результаты моделирования r-процесса с одновре- менным изменением скоростей реакции нейтронного захвата на всех изотопах 187÷193Tb по описанным выше моделям ядерных уровней. Видно, что неопреде-
ленность выбора модели уровней накапливается и в данном случае достигает
50% для рассматриваемых ядер, а для близких к ним по массам до 10 %.