Хорошо известно, что средний кулоновский потенциал нейтрального атома (так называемый статический потенциал):

(14.1)

экспоненциально убывает с расстоянием. Например, V_stat(r) Для атома водорода (в основном состоянии) описывается формулой

(14.2)

    С точки зрения идеи об обобщенном оптическом потенциале (лекция 10) потенциал (14.1) соответствует низшему порядку разложения оптического потенциала по кратности взаимодействия. В этом смысле поляризационный потенциал, к рассмотрению которого мы приступаем, есть потенциал второго порядка. Однако эффекты второго порядка, связанные с поляризуемостью атома, учитываются в нем специфическим образом − в условиях медленного столкновения атома с заряженной частицей, испытывающей на себе это поляризационное взаимодействие. Будем считать эту частицу точечной. Понятие поляризационного потенциала основано на идее о том, что пробная частица (электрон, ион), находясь в какой-то точке своей «траектории», поляризует атом таким образом, что, когда она переходит в другую точку r', атом успевает полностью перестроить свое поляризационное состояние в соответствии с новым положением частицы.
    Мы видим, что в основе концепции поляризационного потенциала лежит представление об адиабатическом характере взаимодействия: изменение взаимодействия частицы с атомом происходит медленно по сравнению с характерными временами (периодами) движения внутриатомных электронов. Такое условие выполняется, когда скорость взаимодействующей с атомом частицы должна быть много меньше, чем скорость электрона в атоме:

Правда, это слишком жесткое требование: при больших параметрах пролета более существенным является ограничение не на линейную, а на угловую скорость v/r.
    Зафиксируем положение пробной частицы r и построим оператор ее взаимодействия с атомом:

(14.4)

Усреднение оператора (r) по основному состоянию атома дает статический потенциал взаимодействия (14.1).
    С точки зрения теории возмущений это есть сдвиг основного уровня атома ΔЕ⁽¹⁾, отнесенный к фиксированной точке r:

ΔЕ(1)(r) = <0|(r)|0> = Vstat(r) .

(14.5)

Рассматривая (14.4) как малое возмущение, найдем сдвиг уровня во втором порядке:

(14.6)

разумеется, здесь под знаком суммы подразумевается и интегрирование по непрерывному спектру атома.
    Пусть пробная частица находится далеко от атома:

Тогда, используя известное разложение

(14.8)

запишем его для случая, r > r_i:

(14.9)

Подставляя (14.9) в (14.4) и далее в (14.6), видим, что главный вклад в потенциал второго порядка дают виртуальные дипольные переходы:

(14.10)

Заметим, что независимо от знака заряда пробной частицы (электрон, ион) поляризационный потенциал (14.10) − это потенциал притяжения. Амплитуда поляризационного взаимодействия просто связана с дипольнои поляризуемостью атома х:

(14.12)

где = е∑_i r_i − оператор электрического дипольного момента атома.
    Главное свойство поляризационного потенциала − его относительное дальнодействие. Будучи эффектом второго порядка он тем не менее гораздо существеннее на больших расстояниях, чем статический потенциал V_stat(r).
    Заметим, что если орбитальный момент атома не равен нулю, то оператор (14.4) дает поправку к V_stat(r) и в первом порядке − за счет квадрупольного взаимодействия:

(14.13)

при больших r оно спадает как 1/r³. Однако это взаимодействие исчезает при усреднении по ориентации момента атома. Поэтому оно проявляется лишь в особых ситуациях, когда момент атома ориентирован.

    На больших расстояниях между атомами их взаимодействие описывается силами Ван-дер-Ваальса. Построим оператор взаимодействия двух атомов, находящихся на фиксированном расстоянии друг от друга:

(14.14)

При R >> а взаимодействия между ядрами компенсируются их взаимодействием с электронной оболочкой, и самым важным становится поляризационное взаимодействие, обусловленное одновременным дипольным возбуждением обоих атомов. Соответствующий член в разложении потенциала (14.14) по мультиполям имеет вид

(14.15)

где

(14.16)

− операторы дипольного момента двух атомов, n − единичный вектор в направлении межъядерной оси.
    В первом порядке теории возмущений оператор (14.15) не дает вклада; во втором − приводит к силам Ван-дер-Ваальса:

    Рассмотрим процесс перезарядки атома водорода при столкновении с протоном:

Пусть R − радиус-вектор, фиксирующий взаимное расположение двух ядер водорода; r_А и r_B − координаты электрона относительно ядер А и В.
    Задача решается в адиабатическом приближении (см., например, [1, § 57]). Стационарные состояния электрона при фиксированном расстоянии между ядрами таковы, что электрон в равной мере принадлежат каждому из ядер. Для простоты опустим интеграл перекрывания волновых функций электрона, локализованного вблизи ядра А и ядра В:

и тогда волновые функции стационарных состояний электрона в рассматриваемой двухцентровои системе («молекулярные орбитали») можно описать простыми комбинациями невозмущенных атомных функций:

ψg(R,r) = 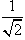[ψ0(rA) + ψ0(rB)] , ψu(R,r) = 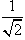[ψ0(rA) − ψ0(rB)] .

(14.20)

    Энергия всей системы Н + Н⁺ как функция расстояния R зависит от симметрии электронной волновой функции (14.20). Для электрона, находящегося на ls-уровне, имеем

Ug(R) = + e1s + ΔV(R) + W(R), Uu(R) = + e1s + ΔV(R) − W(R),

(14.21)

где

(14.22)

− средняя энергия взаимодействия атомного электрона с «чужим» протоном. Величина

(14.23)

не имеет такого простого смысла; она появилась в связи с тем, что волновые функции (14.20) передают эффект «обобществления» электрона в молекулярном ионе (Н + Н⁺).
    По мере сближения ядер качество приближения (14.20) ухудшается: все сильнее искажаются атомные волновые функции электрона; в пределе R → 0 электронная волновая функция совпадает с водородоподной волновой функцией в поле заряда Z = 2. Таким образом, при изменении межъядерного расстояния во всей области 0 < R < ∞ энергетический спектр стационарных состояний электрона в системе (Н + Н⁺) меняется по закону

(14.24)

Рис. 14.1. Корреляционная диаграмма для систем (Н + Н+).

    Общая картина относительного расположения энергетических уровней электрона, находящегося в поле двух ядер, называется диаграммой молекулярных («квазимолекулярных») термов или корреляционной диаграммой. Она показывает, как коррелируют определенные состояния электрона в разъединенных атомах с его состояниями в объединенном атоме (квазимолекуле). Корреляционная диаграмма для системы (Н + Н+) показана на рис. 14.1.
    Вычислим вероятность процесса перезарядки (14.18) для случая далеких (и по-прежнему  медленных: v << v_a) столкновений. Теперь движение ядер относительно друг друга можно рассматривать как классическое прямолинейное движение. Задавая прицельный параметр b, найдем расстояние между ядрами в произвольный момент времени t по формуле

Энергия электрона, находящегося на той или иной молекулярной орбитали (14.20), есть медленно меняющаяся функция времени:

В таком случае временная зависимость волновых функций электрона дается квазиклассическим выражением [13]:

(14.27)

(и аналогично для ψ_u(t,r)).
    Пусть при t → −∞ электрон находился в состоянии Is в поле ядра А. Рассматривая случай далеких столкновений, пренебрежем вкладом всех возбужденных (2s, 2p и т.д.) состояний электрона в атоме. Тогда общее решение «электронной» части задачи в сделанных приближениях имеет вид

(14.28)

Коэффициенты c₁ и с₂ найдем из условия

т.е.

Подставляя (14.30) в (14.28), получаем волновую функцию электрона при t → +∞;

(14.31)

    Таким образом, вероятность перезарядки, т.е. передачи электрона от ядра А ядру В, при далеком медленном столкновении дается формулой

(14.32)

    Чтобы выявить зависимость вероятности ω(b,v) от прицельного параметра b и относительной скорости ядер v, подставим в (14.32) выражения (14.21):

(14.33)

Поскольку мы рассматриваем здесь лишь далекие столкновения, упростим далее это выражение:

(14.34)

Учитывая (14.25) и подставляя (14.34) в (14.32), после интегрирования по t получаем

(14.35)

    Хотя максимум вероятности перезарядки ω(b,v) достигается при значении прицельного параметра
b = (3/2)а, все наше рассмотрение относится лишь к далеким столкновениям (b >> а); как видно из формулы (14.35), с ростом b вероятность перезарядки быстро падает. Что касается ее зависимости от скорости частиц, то в области применимости теории (v << v_а) величина ω(b,v) с ростом v также монотонно падает.
    Корреляционная диаграмма квазимолекулярных термов, изображенная на рис. 14.1, относится лишь к рассматриваемому частному случаю систему (Н + Н⁺), которая обладает рядом специфических свойств − одинаковые ядра, «случайное» вырождение уровней по ℓ в пределе разъединенных атомов. В общем случае картина расположения квазимолекулярных термов сложнее. Особенно интересно и очень важно с физической точки зрения явление пересечения (или, как мы увидим при более внимательном рассмотрении, «квазипересечения») молекулярных термов, когда при некотором значении межъядерного расстояния Rc эффективная потенциальная энергия ядер U₁(R) и U₂(R), соответствующая двум разным электронным состояниям, принимает одно и то же значение:

    На примере системы (Н + Н⁺) мы видели, что понятие эффективной потенциальной энергии ядер U(R) связано с представлением полной волновой функции системы в виде произведения.

Ψ(R,r) = ∑i(R)(R,r)

(14.38)

где (R,r) − это полный набор электронных волновых функций, представляющих собой решение двухцентровой задачи при фиксированном расположении ядер (для нахождения волновой функции электрона, движущегося в поле двух закрепленных точечных зарядов, удобно использовать так называемые кулоновские сфероидальные функции [12]). Считая функции (R,r) известными, мы можем, отправляясь от точного гамильтониана квазимолекулы, получить систему связанных между собой уравнений для функций (R) описывающих движение ядер. При этом уже знакомые нам функции U_i(R) по-прежнему выступают в качестве эффективной потенциальной энергии взаимодействия ядер в «каналах», соответствующих различным состояниям электрона. Однако, в отличии от адиабатического приближения, теперь они, не исчерпывают всей матрицы такого взаимодействия; ее недиагональные элементы обусловленные неадиабатическими слагаемыми в гамильтониане, связывают «каналы» между собой.
 

    Переходы между двумя термами особенно вероятны при их сближении друг с другом, т.е. в окрестности точки пересечения R_c. В связи с этим рассмотрим вопрос о пересечении термов более внимательно. Допустим, что в окрестности точки R_c достаточно рассмотреть лишь два терма 1 и 2 и пренебречь их связью с остальными; им соответствует субматрица эффективного взаимодействия ядер:

(14.39)

причем U₁(R_c) = U₂(R_c) (рис. 14.2, пунктир).
    Диагонализируем матрицу (14.39) в окрестности точки R_c:

(14.40)

    Два значения энергии E(R), даваемые этой формулой, совпадают в некоторой точке R_c лишь при одновременном выполнении двух условии:

Рис. 14.2. Квазипересечение молекулярных термов.

    Случайное выполнение обоих условий (14.41) маловероятно. Может, правда, случиться, что взаимодействие между рассматриваемыми двумя термами отсутствует не только в самой точке R_c, но |и в целой области R в силу каких-то особых правил запрета (связанных с симметрией электронных состояний и т.п.). Во всех других случаях невыполнение комбинированного условия (14.41) означает, что благодаря взаимодействию между термами их фактического пересечения не происходит; имеет место ситуация, изображенная с помощью сплошных линий на рис. 14.2; ее принято называть квазипересечением термов.

    Использование представлений, заимствованных из классической механики, характерно для многих задач квантовой теории медленных столкновений. Сейчас мы рассмотрим еще одну такую задачу, взятую, в отличие от предыдущего параграфа, из ядерной физики.
    Пусть тяжелая заряженная частица заряда Z_х неупруго рассеивается ядром с зарядом Z_А, причем энергия их относительного движения Е меньше высоты кулоновского барьера между ядром и частицей х.

где R − радиус сильного взаимодействия в системе А + х. При таком условии вероятность проникновения частицы в область действия ядерных сил мала, и возбуждение ядра происходит за счет электромагнитного (в основном кулоновского) взаимодействия налетающей частицы с протонами ядра:

(14.43)

На больших расстояниях между частицей х (мы будем считать ее точечной) и ядром А взаимодействие (14.43) сводится к кулоновскому взаимодействию точечных зарядов, которое, разумеется, не может приводить к возбуждению ядра. Поэтому мы исключим его из _Coul:

(14.44)

будем называть оператор (14.44) оператором кулоновского возбуждения ядра.
    Основные закономерности кулоновского возбуждения ядер можно получить с помощью квантовой теории медленных столкновений, считая, что налетающая частица движется по классической траектории согласно законам механики. Пусть нам известна классическая траектория r = r(t) частицы, падающей на ядро с прицельным параметром b. Следовательно, мы знаем оператор кулоновского возбуждения как функцию времени: _exc = V_exc(t). Вероятность перехода ядра из начального состояния |0> в некоторое возбужденное состояние |n> вычислим по теории возмущений:

(14.45)

Подчеркнем: величина Р_n0, даваемая формулой (14.45), есть относительна вероятность того, что медленная заряженная частица, налетая на ядро с определенным прицельным параметром b, индуцирует ядерный переход |0> → |n>. Как известно, в классической механике угол рассеяния θ однозначно определяется прицельным параметром b. Таким образом, формула (14.45) позволяет рассчитывать относительную вероятность перехода |0) → |n> при кулоновском рассеянии частицы на заданный угол:
Р_n0 = Р_n0(θ). При этом мы полагаем, что потери энергии частицы на возбуждение ядра пренебрежимо малы по сравнению с самой энергией:

Дифференциальное сечение возбуждения перехода |0> → |n> есть, таким образом, дифференциальное сечение упругого рассеяния частицы на заданный угол (оно в первом приближении дается формулой Резерфорда), умноженное на относительную вероятность возбуждения:

Упражнения

14.1. Используя приближение малых углов классической теории столкновений (см., например, [10, § 20]), найти дифференциальное сечение рассеяния частиц потенциалом V(r) = -α/r⁴.

14.2. Преобразовать результат (14.32) для случая, когда вероятность перезарядки много меньше единицы; рассмотреть этот случай как самостоятельную задачу, пользуясь теорией возмущений.

14.3. Сравнить возбуждение ядерных переходов «нормальной четности» 0⁺ → J^π, где π = (−1)^J, при неупругом рассеянии быстрых электронов (см. лекцию 8) и в реакции кулоновского возбуждения тяжелыми заряженными частицами считая, что рассеяние электронов обусловлено их кулоновским взаимодействием с протонами ядра. При каких условиях дифференциальные сечения неупругого рассеяния в этих двух случаях выражаются через одни и те же ядерные матричные элементы?