При высоких энергиях, когда дебройлевская длина волны налетающих частиц становится много меньше размеров мишени, а их поглощение в веществе мишени велико, рассеяние частиц носит ярко выраженный дифракционный характер. Простейшей задачей дифракционной теории рассеяния является задача об абсолютно поглощающей («черной») сфере. Рассмотрим ее, пользуясь эйкональным приближением теории потенциального рассеяния (§ 4.2). Для этого представим себе, что частица рассеивается на чисто мнимой прямоугольной потенциальной яме очень большой глубины:

(15.1)

В § 10.4 было показано, что отрицательная величина мнимой части оптического потенциала соответствует поглощению частиц, т.е. их выбыванию из упругого канала с переходом в неупругие каналы.
    Подставляя потенциал (15.1) в (4.35), получаем фазовый сдвиг:

(15.2)

т.е.

(15.3)

    Подставляя это выражение в (4.39), найдем амплитуду рассеяния.
    Рассмотрим предельный случай очень сильного поглощения, |V₀|μa/(ћ²k) когда столь велико, что можно положить

(15.4)

Этот случай соответствует эйконалу абсолютно черной сферы. Для амплитуды рассеяния на этой абсолютно черной сфере получаем

(15.5)

где, согласно (4.30),

Как известно,

Используя это соотношение, получаем:

(15.8)

(15.9)

Рис. 15.1. Угловое распределение частиц при дифракционном рассеянии на абсолютно черной сфере.

График дифференциального сечения (15.9) представлен на рис. 15.1.
    Интегральное сечение упругого рассеяние выра-жается через фазовый сдвиг (см. § 4.3)

Подставляя сюда (15.4), находим

т.е. полное сечение упругого рассеяния равно площади поперечного сечения сферы. Для определения полного сечения взаи-модействия воспользуемся оптической теоремой. Подставляя амплитуду (15.8) в (3.28), получаем

При этом мы воспользовались тем, что

    Сравнивая (15.12) с (15.11), находим сечение всех неупругих процессов (сечение поглощения):

которое оказывается равным полному сечению упругого рассеяния (см. также упражнение 16.2).

    В конце 50-х годов Глаубер и Ситенко одновременно сформулировали теорию дифракционного рассеяния частиц на многочастичных системах − так называемую дифракционную модель многократных столкновений. Эта модель получила широкое применение сначала в физике ядерных реакций, а затем также в физике элементарных частиц и в атомной физике. Рассмотрим ее основные положения, используя для определенности термины ядерной физики [15, 16].
    Дифракционная модель многократных столкновений формулируется соотношением

(15.14)

Рис. 15.2. Многократные столкновения частицы с нуклонами ядра в модели Глаубера-Ситенко.

Оно означает, что фаза χ(b) = χ(b; s₁, ..., s_A), которую приобретает частица, пролетающая через ядро по траектории, характеризуемой прицельным параметром b, есть сумма фаз  χ(b − s_j) , обусловленных взаимодействием этой частицы с каждым из нуклонов ядра (рис. 15.2).
    Соотношение (15.14) предполагает, что все нуклоны ядра в течение времени пролета адрона через ядро оказываются «замороженными», а воздействие каждого из них на пролетающую частицу не зависит от того, какое воздействие оказывают на нее другие нуклоны ядра. При вычислении фазы
χ(b; s₁, ..., s_A) мы пренебрегаем отклонением частицы от прямолинейного движения; поэтому
χ(b; s₁, ..., s_A) зависит только от двумерных координат s_j каждого нуклона: r_j = {s_j,z_j}. Подставляя (15.14) в общую с формулу теории дифракционного рассеяния (4.34):

(15.15)

находим амплитуду рассеяния адрона на ядре:

(15.16)

которая является оператором, действующим в пространстве переменных s₁, ..., s_A. Мы дадим упрощенное изложение дифракционной теории многократных столкно-вений и опустим все, что связано со спиновыми и изоспиновыми переменными нуклонов ядра. Вектор q в формуле (15.16) − это переданный ядру импульс q, составляющей которого вдоль направления движения падающих частиц мы пренебрегаем:

q = {q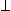,0}.

Выражение

(15.17)

входящее в интеграл (15.16), − профильная функция ядра. Аналогично вводится профильная функция для одного нуклона:

(15.18)

которая связана двумерным преобразованием Фурье (4.37) с амплитудой свободного адрон-нуклонного рассеяния ƒ(q):

(15.19)

(15.20)

    Амплитуда рассеяния адрона на ядре, соответствующая тому, что само ядро переходит при этом из состояния |i> в состояние |f>, вычисляется как матричный элемент от оператора (15.16) в обкладках этих состояний:

(15.21)

    Соотношение (15.21) − основная формула дифрак-ционной теории многократных столкновений. Она позволяет, зная элементарную амплитуду адрон-нуклонного рассеяния ƒ(q) и ядерные волновые функции, вычислить вероятность перехода ядра в любое конечное состояние.
Дифференциальные сечения когерентного и некогерентного рассеяния адрона на ядре вычисляются по формулам

где F_elas(q) ≡ F_ii(q),

(15.23)

    С помощью некоторых дополнительных допущений можно упростить общие формулы дифракционной теории многократного рассеяния, приблизив их к более прозрачным формулам оптической модели. Начнем с рассмотрения когерентного, упругого рассеяния.
    Прямое вычисление амплитуды F_elas(q) по формуле (15.21) с реалистическими волновыми функциями основного состояния ядра Ψ₀(r₁,...,r_A) очень сложно и оказывается практически возможным лишь для легчайших ядер. Вычисление существенно облегчается, если воспользоваться так называемым приближением факторизованной плотности ядра:

(15.24)

здесь ρ_j(r_j) − плотности распределения отдельных нуклонов ядра, нормированные условием

Приближение факторизованной плотности сильнее, чем приближение одночастичной оболочечной модели. Делая его, мы пренебрегаем не только динамическими корреляциями между нуклонами, но и корреляциями, обусловленными тождественностью нуклонов. Bo многих процессах, протекающих при высоких энергиях, корреляции между нуклонами в ядре играют очень важную роль. Однако оказывается, что основные черты адрон-ядерного упругого рассеяния слабо зависят от этих корреляций.
    В приближении факторизованной плотности амплитуда упругого рассеяния имеет вид

(15.26)

где

(15.27)

При получении (15.26) мы положили одинаковыми все :

и все одночастичные плотности

здесь ρ(r) − плотность вещества в ядре, нормированная условием

    Профильная функция γ(b − s) − очень «острая» функция, она быстро затухает на расстояниях, больших радиуса взаимодействия между налетающим адроном и нуклоном a_N. Поэтому при
A >> 1 можно заменить степенную функцию (15.26) экспонентой. Тогда амплитуда упругого рассеяния принимает вид

(15.31)

В показателе экспоненты можно провести интегрирование по переменной z:

Здесь мы ввели новую функцию (функцию толщины)

(15.33)

удовлетворяющую условию нормировки:

    Функция толщины T(s) меняется существенно на расстояниях порядка размеров ядра R. Учитывая неравенство a_N << R, оценим интеграл (15.32) приближенно, для чего вынесем медленно меняющуюся функцию T(s) за знак интеграла. Оставшийся интеграл дает, согласно (15.19), амплитуду адрон-нуклонного рассеяния вперед. В результате F_elas(q) приобретает вид

(15.35)

Заметим, что соотношение a_N << R равносильно утверждению, что элементарная амплитуда ƒ(q) − это медленно меняющаяся функция переданного импульса по сравнению с формфактором нуклонной плотности ядра 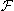_N(q):

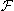N(q) = ∫ρ(r)eiqrd3r = ∫T(b)eiqbd2b.

(15.36)

Воспользуемся оптической теоремой для амплитуды ƒ(q):

здесь σ − полное сечение адрон-нуклонного взаимодействия; α = Reƒ(0)/Imƒ(0) − отношение вещественной и мнимой частей элементарной амплитуды рассеяния на нулевой угол. Подставляя (15.37) в (15.35), запишем амплитуду упругого рассеяния в другом, эквивалентном виде:

(15.38)

Выражения (15.35) и (15.38) называют оптическим пределом для амплитуды адрон-ядерного упругого рассеяния. При σ → 0 они переходят в формулу плосковолнового импульсного приближения:

в противоположном случае очень сильного поглощения (σ >> R²) − в амплитуду рассеяния на абсолютно черной сфере стремится:

    Чтобы сделать аналогию между теорией Глаубера и оптической моделью еще более полной, найдем выражение для эквивалентного одночастичного потенциала V_opt(r); дающего в дифракционном приближении такое же описание рассеяния, что и микроскопическая теория. В потенциальной задаче (при использовании эйконального приближения) фаза рассеяния вычисляется как интеграл от потенциала по прямолинейной траектории движения частицы (формула (4.35)):

(15.41)

Сравнивая (15.41) с формулой оптического предела, где

получим

(15.43)

или же, если вынести медленно меняющийся сомножитель ρ(r) из-под интеграла, получим, что эквивалентный оптический потенциал распределен по ядру так же, как плотность нуклонов:

Vopt(r) = −ƒ(0)ρ(r).

(15.44)

Таким образом, мы снова получили формулу (13.27) для оптического потенциала в приближении Рэлея.

    Рассмотрим неупругое и квазиупругое дифракционное рассеяния частиц составной системой на примере взаимодействия адронов с ядрами. Главная проблема теории неупругого рассеяния адронов состоит в том, как совместить учет многократных столкновений налетающей частицы с нуклонами при ее прохождении через ядро с верным описанием индивидуальных особенностей не только каждого ядра, но и каждого отдельного ядерного перехода, возбуждаемого при неупругом рассеянии падающей частицы. Ключом к решению этой проблемы стало приближение одного неупругого столкновения, введенное Карапетяном, Милеевым и Титаренко (1973 г.) на основе теории Глаубера − Ситенко.
    Приближение одного неупругого столкновения состоит в том, что в амплитуде неупругого рассеяния адрона опускаются вклады многократного многоступенчатого возбуждения ядра; однако учитываются все многократные, столкновения, при которых не происходит перестройки ядра. Это упругое перерассеяние, предшествующее акту неупругого рассеяния или следующее за ним, рассчитывается в тех же упрощающих предположениях, что используются в задаче упругого дифракционного рассеяния: приближение факторизованной плотности, приближение коммутативности между собой амплитуд рассеяния падающей частицы на отдельных нуклонах ядра и т.п.
    Таким образом, амплитуда парциального перехода |0> → |n> записывается в виде

(15.45)

Далее пренебрежем различием между распределением плотности ядра ρ(r) в начальном |0> и конечном |n> состояниях, а недиагональный матричный элемент в (15.45) выразим через плотность перехода:

(15.46)

Тогда амплитуда парциального перехода принимает простой вид:

(15.47)

где

фактор искажений, отражающий эффект упругого перерассеяния в начальном и конечном состояниях.
    В «оптическом пределе» амплитуда (15.47) еще более упрощается:

(15.48)

где σ и α − параметры элементарной двухчастичной амплитуды рассеяния (15.37), а Т(b) − функция толщины (15.33). Если считать, что радиус взаимодействия налетающей частицы много меньше чем размеры ядра, то отсюда получаем

(15.49)

    Выражения близкие к (15.49) можно получить, отправляясь и не от модели Глаубера − Ситенко, а от метода искаженных волн. В импульсном приближении искаженных волн амплитуда процесса (х,х' ) вычисляется как интеграл:

(15.50)

где ƒ_j(q) − амплитуда рассеяния на j-м нуклоне, а

(r) = eikr и (r) = eik'r

(15.51)

искаженные волны налетающей и рассеянной частиц. В приближении высоких энергий факторы искажения и вычисляются как интеграл по прямолинейной траектории движения частицы до и после неупругого столкновения с одним из нуклонов ядра:

(15.52)

где U_i(r) и U_f(r) − оптические потенциалы взаимодействия частицы с ядром в начальном и конечном состояниях. Если же U_i(r) и U_f(r) взять в приближении Рэлея (15.44), а также пренебречь искривлением траектории частицы при вычислении фактора искажения, то для (15.50) получим

(15.53)

где ρ_i(r) и ρ_f(r) − плотности ядра в начальном и конечном состояниях. Наконец, положив здесь
ρ_i(r) = ρ_f(r), получаем

(15.54)

Выражение (15.54) отличается от (15.49) фактором exp{iq_zz) содержащим продольную составляющую переданного импульса

q_z = (qk)/k.

    Обратимся теперь к квазиупругому некогерентному рассеянию. Для вычисления сечения надо, согласно (15.21) и (15.23), просуммировать вероятности переходов на все возбужденные состояния ядра-мишени:

(15.55)

Выражение (15.55) написано не совсем точно, так как вектор переданного импульса q зависит (при фиксированном значении угла рассеяния) от энергии возбуждения ядра ε_f. Однако при больших энергиях налетающих частиц эта зависимость невелика, и мы ею пренебрежем. Воспользуемся соотношением полноты

Тогда вся бесконечная сумма сведется к интегралам, куда войдут лишь матричные элементы по основному состоянию ядра

(15.57)

Далее примем приближение факторизованной плотности (15.24) и перейдем к оптическому пределу. В этом случае сечение некогерентного рассеяния дается выражением

15.58

где χ_opt(b) − фаза упругого рассеяния (15.42), а Ω(b,b' ) − новая функция, определенная соотношением

    Выражение (15.58) можно упростить дальше, если учесть, что ввиду малости радиуса адрон-нуклонного взаимодействия функция Ω(b,b' ) отлична от нуля лишь для близких значений аргументов b и b' :

(15.60)

Если взять параметры нуклон-нуклонного взаимодействия из эксперимента, то величина показателя экспоненты в выражении (15.60) (взятого в квадратные скобки) оказывается заметно меньше единицы. Это позволяет разложить экспоненту в степенной ряд и ограничиться его несколькими первыми членами:

Первое слагаемое, пропорциональное элементарному сечению нуклон-нуклонного рассеяния (dσ/dΩ)₀  = |ƒ(q)|², описывает однократное квазиупругое рассеяние падающей частицы на нуклонах периферического кольцевого слоя, окаймляющего ядро в плоскости, перпендикулярной направлению падающего пучка. Эффективное число нуклонов, участвующих в квазиупругом рассеянии, дается, согласно (15.61), формулой:

Следующие слагаемые в (15.61) соответствуют двукратному, трехкратному квазиупругому рассеянию и т.д. При малых углах их вклад незначителен по сравнению с вкладом однократного рассеяния, однако они медленнее, чем первое слагаемое, затухают с увеличением угла рассеяния.

    В § 15.1 мы получили дифференциальное сечение упругой дифракции быстрых частиц на сильно поглощающей (абсолютно черной) сфере. Точно такой же результат следует из модели Глаубера−Ситенко (сравним (15.8) и (15.40)). Таким образом, в пределе очень сильного поглощения угловое распределение упруго рассеянных частиц становится нечувствительным к индивидуальным особенностям мишени и описывается универсальной формулой, куда входит лишь параметр размеров мишени:

    Сейчас, отправляясь от «микроскопического» подхода, изложенного в предыдущих двух параграфах, мы покажем, что в условиях сильного поглощения дифференциальное сечение неупругой дифракции также нечувствительно к структуре мишени, а угловое распределения неупруго рассеянных частиц определяется лишь мульти-польностью перехода и размерами мишени.
    Для определенности будем говорить о рассеянии быстрых нейтронов ядром, спин которого в основном состоянии равен нулю. Пусть j − спин конечного состояния ядра, а М − его проекция на направление падающего пучка. Согласно (15.54), в оптическом пределе амплитуда неупругого рассеяния, соответствующая переходу |0> → |jM>, дается выражением

(15.64)

здесь мы положили взаимодействие налетающей частицы со всеми нуклонами ядра одинаковым и вынесли элементарную амплитуду взаимодействия ƒ₀(q) за знак суммы.
    Далее будем следовать работе [9]. Выделим в переходной плотности ядра угловую часть:

(15.65)

и выразим сферическую функцию Y_jM(θ,φ) через присоединенный полином Лежандра:

(15.66)

(15.67)

    Интегрирование в (15.64) по азимутальному углу вектора b дает цилиндрическую функцию Бесселя: