§ 8.2. Упругое рассеяние быстрых электронов на атомах
Применим полученные результаты к рассеянию электронов на атомах. При
этом будем стремиться к тому, чтобы представить их в форме, не зависящей
от конкретного вида атомных волновых функций. Как и в предыдущем
параграфе, опустим все, что касается обменного рассеяния
(тождественности частиц) и взаимодействий, зависящих от спинов.
Оператор возмущения
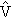 есть в нашем случае оператор взаимодействия
налетающего электрона с ядром атома и всеми Z электронами атома: есть в нашем случае оператор взаимодействия
налетающего электрона с ядром атома и всеми Z электронами атома:
 |
(8.24) |
а борновская амплитуда рассеяния выражается через интеграл по
координате рассеиваемого электрона r и координатам атомных электронов {r1,...,
rZ}:
 |
(8.25) |
Первое слагаемое в (8.25), обусловленное взаимодействием налетающего
электрона с ядром атома, отлично от нуля только в случае упругого
рассеяния; при этом интегрирование по переменной г дает борновскую
амплитуду рассеяния электрона на точечном заряде Ze (см. (2.27)).
Отложим до следующего параграфа исследование формулы (8.25) в случае
неупругого рассеяния и займемся борновской амплитудой упругого
рассеяния:
 |
(8.26) |
При получении (8.26) из (8.25) мы воспользовались вспомогательным соотношением
 |
(8.27) |
и ввели обозначение матричного элемента по атомным волновым функциям:
 |
(8.28) |
Легко видеть, что входящий в (8.26) диагональный матричный элемент
(8.28) − это фурье-образ плотности электронов в основном состоянии атома
рв(г):
 |
(8.29) |
 |
(8.30) |
Определим формфактор плотности электронов соотношением
 |
(8.31) |
и выразим через него борновскую амплитуду упругого рассеяния электронов:
 |
(8.32) |
Тогда дифференциальное сечение упругого рассеяния вычислится по формуле
 |
(8.33) |
где (dσ/dΩ)R − дифференциальное сечение рассеяния электронов на точечном единичном заряде (формула Резерфорда (2.28)).
В обычных условиях распределение электронной плотности в основном состоянии атома сферически-симметрично:
тогда и формфактор (8.31) зависит лишь от модуля передаваемого импульса:
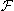 e(q) → e(q) →
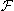 e(q) e(q) |
(8.35) |
Следовательно, в таком случае (а также в случае аксиально-симметричного относительно импульса
ki распределения плотности ρе(r)) рассеяние электронов не зависит от азимутального угла φ.
Согласно определению (8.31), формфактор
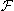 e(q) нормирован условием e(q) нормирован условием
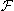 e(0) = 1, а при малых q выражается через среднеквадратичный радиус
электронной оболочки атома: e(0) = 1, а при малых q выражается через среднеквадратичный радиус
электронной оболочки атома:
 |
(8.36) |
Подставляя (8.36) в (8.32), видим, что, хотя атом − это в среднем
нейтральная система, вероятность рассеяния электрона на атоме отлична от
нуля даже при бесконечно малых углах рассеяния:
 |
(8.37) |
в этом проявляется дальнодействующий характер кулоновского
взаимодействия. Не следует, однако, воспринимать (8.37) как надежный в
количественном отношении результат: борновская амплитуда (8.32)
вещественна, и ее значение в нуле не удовлетворяет оптической теореме.
§ 8.3 Возбуждение дискретных уровней атомов быстрыми электронами.
Понятие неупругого формфактора. Правила отбора при малом передаваемом
импульсе. Энергетическая зависимость вероятности оптически разрешенных
переходов
Вернемся к общему выражению (8.25) для борновской амплитуды рассеяния
электрона на атоме. Если |n> ≠ |0>, то первое слагаемое в (8.25),
обусловленное взаимодействием налетающего электрона с ядром атома,
пропадает. Амплитуда неупругого рассеяния электрона, при котором атом
совершает переход из состояния |0> в состояние |n>, а также,
соответствующее парциальное дифференциальное сечение рассеяния выражаются через
неупругий электронный формфактор атома
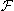 n0(q): n0(q):
 |
(8.38) |
 |
(8.39) |
Мы определили неупругий формфактор соотношением
 |
(8.40) |
В различных задачах атомной физики он используется как модельно
независимая структурная характеристика, отражающая все свойства волновых
функций состояний |0> и |n>, которые в первом порядке теории возмущений
проявляются в переходе |0> → |n>.
Рассмотрим процесс неупругого рассеяния, когда передаваемый импульс мал:
где а − некоторый параметр, характеризующий средние размеры атома.
Разлагая входящую в 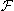 n0(q) экспоненту в ряд Тейлора и учитывая
ортогональность атомных волновых функций |0> и |n>, получаем, что при
малых q неупругий формфактор n0(q) экспоненту в ряд Тейлора и учитывая
ортогональность атомных волновых функций |0> и |n>, получаем, что при
малых q неупругий формфактор 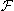 n0(q) выражается через матричный элемент
оператора электрического дипольного момента атома: n0(q) выражается через матричный элемент
оператора электрического дипольного момента атома:
 |
(8.42) |
где
 |
(8.43) |
Таким образом, если передаваемый импульс мал, то при неупругом
рассеянии электронов преимущественно возбуждаются переходы |0> → |n>, удовлетворяющие правилам отбора для электромагнитных Е1-переходов:
 |
(8.44) |
Такие переходы называются оптически разрешенными или Е1-переходами.
Состояния дискретного спектра атома − это (за исключением особого
случая атома водорода) состояния с определенным значением углового
момента. Опуская все, что связано со спином атомных электронов и
налетающего электрона, рассмотрим возбуждение уровня с определенным
орбитальным моментом Ln (пусть при этом L0 − орбитальный момент атома в
основном состоянии):
|
A(L0) + е → A*(Ln) + е' . |
(8.45) |
Если ориентация углового момента L0 неопределенна, а детектор реакции
(8.45) нечувствителен к ориентации момента Ln, то дифференциальное
сечение парциального перехода (8.39) вычисляется усреднением по всем
направлениям L0 и суммированием по всем направлениям Ln:
 |
(8.46) |
Разложим оператор по мультиполям (см. (3.4)):
 |
(8.47) |
здесь  j и j и
 q − единичные векторы в направлении векторов
rj и q, θqrj
− угол между этими направлениями. По теореме Вигнера − Эккарта [1,
(56.5)] получаем q − единичные векторы в направлении векторов
rj и q, θqrj
− угол между этими направлениями. По теореме Вигнера − Эккарта [1,
(56.5)] получаем
 |
(8.48) |
где приведенный матричный элемент
 |
(8.49) |
будем называть мультипольным формфактором перехода.
Подставляя (8.48) в (8.46) и используя известные свойства
коэффициентов Клебша − Гордона [1, (41.19) и (Д2.3)], выразим
дифференциальное сечение парциального перехода |0> → |n> через
мультипольные формфакторы перехода:
 |
(8.50) |
здесь мы воспользовались также, формулой [1, (Д7.15)] для выполнения
суммирования по магнитному квантовому числу μ; благодаря такому
суммированию в (8.50) вьшала зависимость от направления вектора
переданного импульса q.
Мультипольные формфакторы (8.49) ведут себя при малых q согласно степенному закону:
 |
(8.51) |
Поскольку дифференциальное сечение (dσ/dΩ)R пропорционально 1/q4,
получаем, что дифференциальные сечения парциальных переходов
мультипольности λ, ведут себя при малых q согласно закону:
 |
(8.52) |
Отсюда, как и из (8.42), снова видно, что в реакции (е,е' ) при малых
q в спектрах возбуждения атома доминируют El-переходы. Заметим также,
что при неупругом рассеянии, в отличие от упругого рассеяния,
минимальный переданный импульс qmin = ki − kf всегда больше нуля.
Поэтому дифференциальное сечение любого парциального перехода (е,е'
), в отличие от (dσ/dΩ)R, никогда не обращается в бесконечность при θ = 0.

Рис. 8.1. Кинематика рассеяния электрона на атоме. |
Исследуем, как зависит вероятность оптически разрешенных переходов от
энергии налетающих электронов. Полное сечение парциального перехода |0> → |n> вычисляется интегрированием дифференциального
сечения рассеяния dσn/dΩ по всем направлениям вылета рассеянного
электрона:
Поскольку в борновском приближении dσn/dΩ зависит от углов рассеяния электрона через переданный
импульс q то удобно перейти в (8.53) к интегрированию по q (см. (2.24)):
 |
(8.54) |
здесь мы использовали соотношение
 |
(8.55) |
следующее из треугольника векторов ki, kf и
q (рис. 8.1). Если энергия
возбуждения атома εn много меньше, чем энергия налетающих электронов Е,
то пределы интегрирования в (8.54) можно заменить их приближенными
значениями:
θ = 0 qmin = ki − kf →

θ = π qmin = ki − kf →
 |
(8.56) |
При малых q дифференциальное сечение оптически разрешеного перехода ведет себя, согласно (8.52), как
Чтобы фиксировать в (8.57) коэффициент пропорциональности, удобно
вернуться к соотношениям (8.46), (8.40) и (8.42). В борновском
приближении переходы |0L0M0> → |nLnMn> подчиняются строгому правилу
отбора по проекции момента на направление вектора q:
а дифференциальное сечение оптически разрешенного перехода при малых q выражается через матричный элемент оператора проекции электрического дипольного момента атома на
ось квантования (т.е. на направление переданного импульса q):
 |
(8.59) |
где zj − проекция радиус-вектора атомного электрона на ось z. Этот же
матричный элемент входит в так называемую силу осциллятора
электромагнитного Е1-перехода:
 |
(8.60) |
где mе − масса электрона. Подставляя (8.59) в (8.39), получаем
 |
(8.61) |
Из (8.56) видно, что при малых углах рассеяния линейная аппроксимация
формфактора 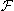 n0(q), а следовательно, и формула (8.57) работают тем
лучше, чем больше энергия Е налетающего электрона. С другой стороны,
именно область самых малых углов дает основной вклад в интеграл (8.54)
Если распространить зависимость (8.57) на всю область интегрирования qmin ≤
q ≤ <qmах, то для парциального сечения оптически
разрешенного перехода получаем следующую аппроксимацию: n0(q), а следовательно, и формула (8.57) работают тем
лучше, чем больше энергия Е налетающего электрона. С другой стороны,
именно область самых малых углов дает основной вклад в интеграл (8.54)
Если распространить зависимость (8.57) на всю область интегрирования qmin ≤
q ≤ <qmах, то для парциального сечения оптически
разрешенного перехода получаем следующую аппроксимацию:
 |
(8.62) |
Эта формула называется формулой Бете.
|
![]() − гамильтониан свободной мишени, его собственные значения εn и
собственные функции
− гамильтониан свободной мишени, его собственные значения εn и
собственные функции ![]() − оператор кинетической энергии частицы, а V = V(ξ,r) − оператор ее взаимодействия с мишенью. Тогда полный гамильтониан
системы можно записать в виде
− оператор кинетической энергии частицы, а V = V(ξ,r) − оператор ее взаимодействия с мишенью. Тогда полный гамильтониан
системы можно записать в виде![]() − оператор возмущения этой системы.
− оператор возмущения этой системы.![]() f
= kf / | kf |. Таким образом, в качестве
dγ в (8.7)
подставляем элемент телесного угла dΩ = sin θ dθ
dφ, где θ и φ −
полярный и азимутальный углы рассеяния. Итак, плотность скорости
перехода |0> → |n> в интересующем нас случае дается выражением
f
= kf / | kf |. Таким образом, в качестве
dγ в (8.7)
подставляем элемент телесного угла dΩ = sin θ dθ
dφ, где θ и φ −
полярный и азимутальный углы рассеяния. Итак, плотность скорости
перехода |0> → |n> в интересующем нас случае дается выражением![]() (r,ξ); важно, чтобы
при этом выполнялось условие полноты:
(r,ξ); важно, чтобы
при этом выполнялось условие полноты:![]() (r,ξ) нормировать по-другому, например
(r,ξ) нормировать по-другому, например
![]() (r,ξ) не имеет никакого значения для получения правильного окончательного
результата, если одновременно с этим − в соответствии с условием (8.13) −
устанавливается и явный вид плотности конечных состояний ρ(n,kf).
(r,ξ) не имеет никакого значения для получения правильного окончательного
результата, если одновременно с этим − в соответствии с условием (8.13) −
устанавливается и явный вид плотности конечных состояний ρ(n,kf).![]() При выбранной нами нормировке этой функции (8.8)
При выбранной нами нормировке этой функции (8.8)
![]() (ξ,r) → V(r), pf → рi), формулы (8.23) и (8.22) переходят в
формулы (2.4) и (1.34) теории потенциального рассеяния.
(ξ,r) → V(r), pf → рi), формулы (8.23) и (8.22) переходят в
формулы (2.4) и (1.34) теории потенциального рассеяния.




























