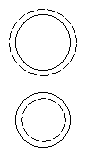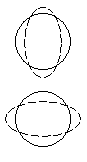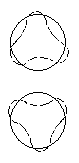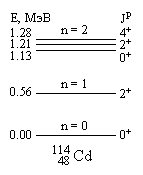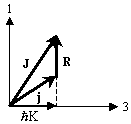
По мере удаления от заполненных оболочек минимум потенциальной энергии может соответствовать деформированному ядру. У несферического ядра изменяются одночастичные уровни, меняется частота колебаний, появляются вращательные степени свободы. На рис.1 показано аксиально-симметричное ядро. Оно может вращаться только вокруг оси перпендикулярной к оси симметрии.
  Оператор ₃ орбитального момента количества движения вдоль оси 3 имеет вид

В силу аксиальной симметрии волновая функция ψ не должна зависеть от угла φ

Поэтому для аксиально-симметричного ядра ₃ = 0 и вращение вокруг оси 3 не меняет квантового состояния системы.
    Для ядер, имеющих в основном состоянии спин J = 0, возбужденные состояния имеют только четные значения спина J = 0, 2, .... Объясняется это тем, что сферические гармоники с нечетным J имеют отрицательную четность, т.е. волновая функция меняет знак при отражениии относительно плоскости 1-2 и поэтому не может быть собственной функцией в случае аксиально- симметричного ядра.
     Энергия вращательных состояний четно-четных деформированных аксиально-симметричных ядер описывается соотношением

где - момент инерции ядра относительно оси 1 или 2, J - спин ядра, пробегающий   значения 0, 2, 4, .... На рис. 2 показан вращательный спектр сильно деформированного ядра ¹⁷⁰Hf.

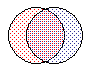
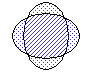
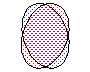
   У сферических ядер существуют колебательные возбуждения, приводящие к деформации поверхности ядра. Возможны монопольные (J = 0), квадрупольные (J = 2), октупольные (J = 3) и т.д. колебания (см. рис. 3). Дипольные колебания отстутствуют, т.к. они соответствуют просто перемещению ядра, при котором ядро не возбуждается.

монопольные квадрупольные октупольные Рис. 3. Колебательные возбуждения четно-четных сферических ядер

    Если ядро способно совершать гармонические колебания какой-то одной мультипольности, например квадрупольные колебания, то их энергия определяется соотношением

E = nω,

где n - целое число (число квадрупольных фононов), ω- энергия одного фонона. Таким образом, для фононов одной мультипольности спектр возбуждений эквидистантен. Спин-четность квадрупольного фонона 2⁺. Двухфононные возбуждения дожны иметь спины и четности 0⁺, 2⁺, и 4⁺. Спины 1 и 3, получающиеся векторным сложением спинов двух фононов, запрещены статистикой Бозе-Эйнштейна. На рис. 4 показан спектр фононных возбуждений четно-четного сферического ядра ¹¹⁴Cd.
    При энергии возбуждения > 10 МэВ в ядрах появляются возбуждения, связанные с разделением протонной и нейтронной компонент - электрические дипольные E1 (гигантский дипольный резонанс), электрические квадрупольные E2, магнитные дипольные (M1) (см рис. 5). Гигантский дипольный резонанс прявляется как широкий пик в сечении поглощения -квантов атомными ядрами.

электрический дипольный резонанс (E1) электрический квадрупольный резонанс (E2) магнитный дипольный резонанс (M1) Рис. 5. Резонансы, связанные с поляризацией протонной и нейтронной компонент. Красным и синим цветов схематически показаны протонная и нейтронная компоненты

    Модель, которая позволила одновременно учесть как одночастичные так и коллективные степени свободы ядра - обобщенная модель была предложена в начале 50-х годов Д. Рейнуотером, О. Бором и Б. Моттельсоном. В этой модели предполагается сильная связь внешних по отношению к заполненным оболочкам нуклонов с остовом, что может приводить к устойчивой равновесной деформации ядра. Движение остова описывается в гидродинамической модели. Одночастичные состояния рассчитываются в деформированном потенциале.
    Если четно-нечетное ядро представляет собой деформированный аксиально-симметричный бесспиновый остов плюс один валентный нуклон, то спектр возбужденных состояний такого ядра можно описать формулой, аналогичной (1)

где E_одн - энергия одночастичного состояния. На рис. 7 показаны энергетические уровни ядра ²⁴⁹Bk. В уровнях можно выделить три вращательные полосы, соответствующим различным значениям полного момента вдоль оси симметрии (K = 7/2⁺, 3/2^-,5/2⁺).

Рис. 7. Энергетические уровни 249Bk. Справа выделены 3 вращательные полосы. Энергии уровней даны в кэВ См. дополнительно "Коллективные возбуждения ядер"
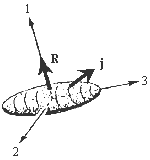
	Рис. 6. Вращательные и одночастичные степени свободы. R - коллективный момент количества движения, j - одночастичный момент количества движения валентного нуклона, J - полный момент количества движения, K - собственное значение полного момента J вдоль оси симметрии 3