Модель ядерных оболочек. Одночастичные состояния

В модели ядерных оболочек нуклоны рассматриваются как независимые частицы в самосогласованном потенциале, создаваемом всей совокупностью нуклонов в ядре. Уровни энергии нуклонов E_i определяются собственными значениями решений уравнения Шредингера

Ĥψ_i= E_iψ_i; Ĥ = + ,

(1)

где ψ_i – волновая функция нуклона с энергией E_i, Ĥ – оператор гамильтона, и – операторы кинетической и потенциальной энергии.
В простейших моделях сферических ядер потенциал V(r) выбирают в виде потенциала трехмерного гармонического осциллятора, либо прямоугольной потенциальной ямы (рис.1).
Осцилляторный потенциал можно записать в виде

(2)

где μ – приведенная масса нуклона, ω – осцилляторная частота (ħω ≈ 41A^-1/3),
V₀ ≈ 50 МэВ. Для потенциала гармонического осциллятора спектр энергетических уровней эквидистантный и имеет следующий вид:

E_i = E_N = ħω(N + 3/2),

(3)

где N = 2n + l – осцилляторное главное квантовое число, n – радиальное квантовое число (число узлов функции, кроме нуля), l – орбитальное квантовое число.
Потенциал прямоугольной потенциальной ямы

V_пя(r) = {	-V₀, r < R	(4)
	0, r > R

Потенциал Вудса-Саксона

V_В-С(r) = -V₀/[1 + exp(r - R/a)],

(5)

где V₀ – глубина потенциала, R = r₀A^1/3 – радиус ядра и a – параметр, характеризующий диффузность (размытие) края потенциала.

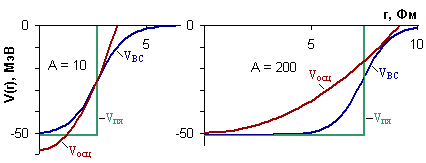Рис. 1. Осцилляторный потенциал, прямоугольная потенциальная яма и потенциал Вудса-Саксона. Видно, что в легких ядрах реалистический потенциал лучше воспроизводится осцилляторным, а в тяжелых - прямоугольной потенциальной ямой

Потенциал Вудса-Саксона представляет нечто среднее между осцилляторным потенциалом и потенциалом прямоугольной ямы. В потенциале Вудса-Саксона снимаются вырождения, свойственные гармоническому осциллятору. Однако реалистический потенциал (5), также как и осцилляторный потенциал, не в состоянии объяснить наблюдаемые в эксперименте магические числа нуклонов.
Решение проблемы было найдено М. Гепперт-Майер и Дж. Иенсеном, которые добавили к центрально-симметричному потенциалу V(r) спин-орбитальное взаимодействие.

V_ls(r) = f(r).

(6)

Спин-орбитальное взаимодействие приводит к расщеплению уровня с данным значением l на два состояния

l + 1/2 и l - 1/2.

При этом состояние с l + 1/2 смещается вниз по энергии, а состояние с l - 1/2 - вверх. Величина спин-орбитального расщепления уровней пропорциональна величине орбитального момента l. Поэто уровни с большими значениями орбитального момента l > 3 сильно смещаясь вниз по энергии оказываются среди уровней предыдущей оболочки, что позволяет правильно воспроизвести магические числа.
Для протонов в самосогласованый потенциал должен быть включен также кулоновский потенциал.

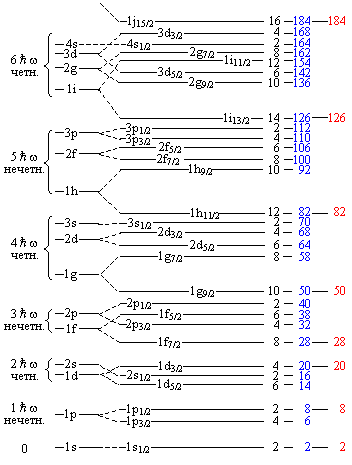Рис. 2. Одночастичные уровни в оболочечном потенциале. Приведено схематическое изображение уровней в потенциале Вудса-Саксона: слева без учета спин-орбитального взаимодействия, справа - с учетом. Фигурные скобки объединяют уровни, входящие в одну осцилляторную оболочку. Черным цветом дано число вакантных мест для нуклонов одного сорта, в синим приведено полное число частиц, красным указаны магические числа

Cостояния нуклонов характеризуются квантовыми числами, которые определяют физические величины, сохраняющиеся при движении в сферически-симметричном поле (см. рис. 2). Обозначения состояний - 1d_5/2 означает, что радиальное квантовое число n = 1, орбитальный момент l = 2 (d-состояние), полный момент j = l + s = 5/2.
В оболочечной модели спин ядра складывается из суммы спинов и орбитальных моментов отдельных нуклонов. Принцип Паули и специфика ядерного взаимодействия приводят к тому, что все четно-четные ядра имеют полный момент (спин) равный 0. Четность ядерного состояния определяется произведением внутренних четностей нуклонов на четности волновых функций, описывающих движение нуклонов относительно общего центра инерции. Внутренняя четность нуклонов принята положительной. Четности ядерного состояния определяется соотношением

(7)

где l_i – орбитальный момент i-го нуклона.
Оболочечная модель во многих случаях хорошо воспроизводит экспериментальные значения спинов и четностей, электрических квадрупольных и магнитных моментов атомных ядер, средние времена жизни β-радиоактивных ядер, объясняет распределение ядер изомеров.

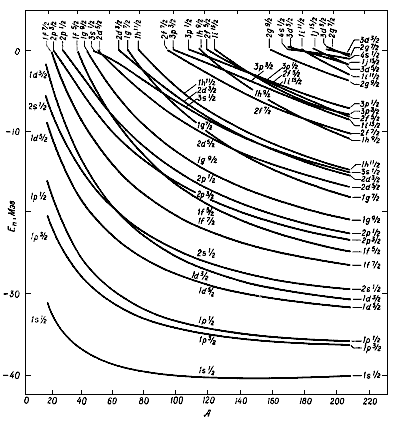Рис. 3. Зависимость энергии нейтронных одночастичных состояний от массового числа

На рис. 3 показаны результаты расчетов нейтронных одночастичных состояний с потенциалом Вудса-Саксона, с небольшой зависимостью его глубины от нейтронного избытка. Радиус ядерного потенциала пропорционален A^1/3. Это приводит к тому, что с ростом A уменьшается расстояние между одночастичными состояниями. Кроме увеличения плотности одночастичных состояний с ростом A, видно, что меняется последовательность состояний.
Плотность одночастичных протонных состояний больше чем нейтронных, а их последовательность для оболочек выше четвертой иная, что обусловленно дополнительным вкладом кулоновского потенциала.

Основные положения одночастичной оболочечной модели

Суммарный момент основного состояния четно-четного ядра (N и Z - четные числа) равен 0.
Суммарный момент основных состояний ядер с нечетным A равен полному моменту j неспаренного нуклона.
Правило хорошо выполняется для ядер, у которых сверх заполненного состояния есть еще один нуклон, либо для заполнения последнего состояния недостает одного нуклона. Недостающий нуклон называется дыркой и момент ядра определяется спином и четностью этого недостающего нуклона.
Суммарный момент нечетно-нечетных ядер, неспаренные нуклоны которого находятся в одинаковых состояниях, равен удвоенному полному моменту неспаренного нуклона.
Энергия уровня с данным n растет с ростом l.
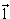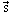Спин орбитальное взаимодействие для параллельных и больше, чем для антипараллельных.

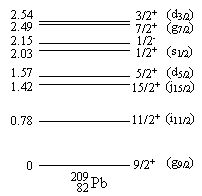Рис. 4. Возбужденные уровни ²⁰⁹Pb

    Наилучшие предсказания оболочечная модель дает для ядер вблизи заполненных оболочек, для которых самосогласованный потенциал сферически-симметричный. Простейший вариант оболочечной модели – одночастичная оболочечная модель.
    На рис. 4 показаны возбужденные состояния дважды магического ядра с одним валентным нуклоном ²⁰⁹Pb. Большинство состояний (кроме 1/2^-) описываются одночастичной оболочечной моделью.
    Наряду со сферическими существуют деформированные ядра. Впервые расчеты одночастичных состояний с использованием деформированного аксиально-симметричного потенциала были выполнены в 1955 году C.Нильссоном .
    Деформированный потенциал Нильссона:

(8)

где x₁, x₂ и x₃ - координаты нуклона во внутренней системе координат.
Первый член в выражении (8) является потенциалом деформированного трехмерного гармонического осциллятора, частоты колебаний которого в направлении оси симметрии (₃) и в направлении перпендикулярном к ней () не совпадают между собой. К нему добавляется обычный спин-орбитальный член и член, который учитывает реальную радиальную зависимость оболочечного потенциала, опуская вниз одночастичные уровни энергии с большим орбитальным моментом l (D < 0). Деформация ядра частично снимает вырождение по j. Однако, сохраняется вырождение по знаку проекции j₃ на ось симметрии ядра. Положения одночастичных уровней в потенциале Нильссона в зависимости от деформации показаны на рис. 5.

Рис. 5. Одночастичные уровни энергии в потенциале Нильссона

ЗАДАЧИ

Модель оболочек
Обобщенная модель ядра