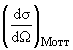Для детального исследования внутренней структуры ядер используют электроны c энергией  >100 МэВ.
    Пионерские исследования рассеяния электронов атомными ядрами были выполнены Р. Хофштадтером.
    По современным представлениям электрон считается бесструктурным (точечным) объектом R < 10^-3 Фм. Взаимодействие электрона с ядром описывается квантовой электродинамикой. Для того, чтобы исследовать электромагнитную структуру ядра необходимо, чтобы длина волны электрона была меньше его размеров.
    При описании рассеяния электронов на атомных ядрах необходимо учесть некоторые дополнительные факторы.

1. Электрон обладает спином (s_е = 1/2).
2. Энергия налетающего электрона может быть сравнима или даже превосходить энергию покоя ядра.

    Дифференциальное сечение рассеяния точечных частиц со спином 1/2 и зарядом Q = -e на точечной бесспиновой частице-мишени описывается формулой Мотта

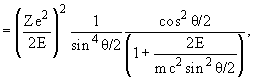(1)

где Z - атомный номер ядра, E - энергия падающего электрона, v = ·c, θ - угол рассеяния электрона, q - переданный ядру четырех-импульс, m - масса ядра.

где E_i, E_f, _i, _f - энергии и импульсы рассеиваемого электрона в начальном и конечном состояниях.
    Формула Мотта получена при следующих предположениях.

1. Ядро и электрон точечные (R_ядра = 0, R_е = 0).
2. Спин ядра и магнитный момент ядра равны 0 (s_ядра= 0, μ_ядра= 0).
3. Спин электрона s_е = 1/2. Величина магнитного момента электрона равен магнетону Бора
   (μ_е= μ_B = eћ/2m_ec).
4. Механизм реакции - упругое рассеяние электронов на ядре.

    В нерелятивистском пределе формула Мотта переходит в формулу Резерфорда.
    Если исследуемый объект (ядро) не точечный, то расчеты по формуле Мотта дают завышенные по сравнению с экспериментом значения дифференциального сечения. Структура ядра описывается с помощью форм-фактора F(q²). Формфактор описывает отклонение размеров ядра от точечного.

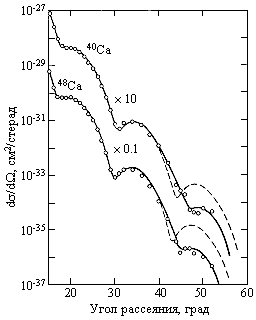Рис. 1. Зависимость дифференциального сечения рассеяния электронов с энергией 750 МэВ на ядрах 40Ca и 48Ca от угла рассеяния. Сечение для 40Ca увеличено в 10 раз, а для 48Ca уменьшено в 10 раз

Для упругого рассеяния в первом приближении форм-фактор зависит только от квадрата переданного импульса и связан с плотностью распределения ядерной материи ρ(r) соотношением

    Сравнивая экспериментально измеренное сечение упругого рассеяния электронов с сечением, рассчитанным по формуле Мотта, вычисляется форм-фактор ядра. Свободные параметры плотности распределения электрического заряда подбираются так, чтобы подогнать вычисленные по формуле (4) значения форм-фактора к полученным в эксперименте. На рис. 1 показаны результаты измерения дифференциального сечения рассеяния электронов с энергией 750 МэВ на ядрах ⁴⁰Ca и ⁴⁸Ca, обработка которых позволяет рассчитать значения форм-фактора и получить информацию о распределении плотности электрического заряда в ядре. Простейшим приемлемым приближением распределения ядерной материи является распределение Ферми (рис.2).

где ρ₀ - плотность ядерной материи в центре ядра, R - радиус ядра - расстояние, на котором плотность ядерной материи спадает в два раза, a - параметр диффузности.
    Для ядер, расположенных вблизи долины стабильности, были установлены следующие закономерности.

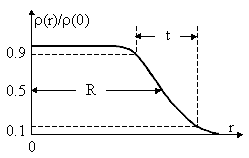Рис. 2. Распределение Ферми

• Пространственное распределение протонов и нейтронов для ядер вблизи долины стабильности практически совпадают.
• Плотность ядерной материи в центре ядра ρ₀ приблизительно одинакова у всех ядер и составляет ~ 0.17 нукл./Фм³ (см. рис.2).
• Толщина поверхностного слоя t
  (спад плотности от 0.9ρ₀ до 0.1ρ₀) у всех ядер примерно одинакова t = 4.4a = 2.4 Фм.
• Величина радиуса ядра определяется числом нуклонов в ядре, R = 1.3A^1/3 Фм (см. рис.4).

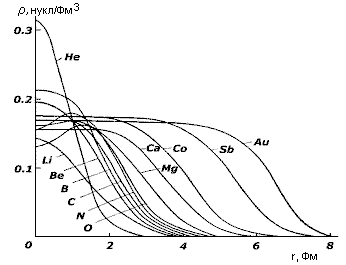
  Рис. 3. Плотность распределения ядерной материи

    Атомные ядра вблизи долины стабильности представляют собой довольно компактные объекты. Их радиусы меняются от 2-3 Фм для самых легких ядер до 7-8 Фм для самых тяжелых.

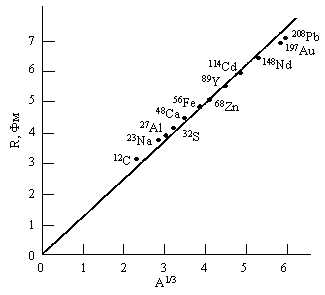Рис. 4. Радиусы ядер, полученные в экспериментах по рассеянию электронов.

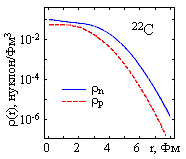Рис. 5. Нейтронный слой у ядра 22С

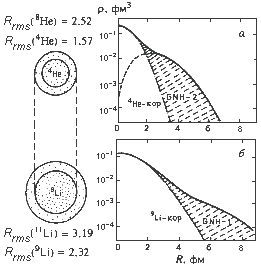
    Однако для ядер, удаленных от долины стабильности, ситуация иная. Для некоторых ядер, перегруженных нейтронами (протонами), наблюдается так называемый нейтронный (протонный) слой - область вблизи поверхности ядра, в которой с учетом фактора нормировки N/Z ρ_n>ρ_p (ρ_p>ρ_n) (см. рис.5). В легких ядрах с большим отношением N/Z было открыто нейтронное гало. Нейтронное гало наблюдается в ядрах, у которых энергия связи нейтрона B_n < 1-1.5 МэВ. Оказалось, что в гало-ядрах наряду с кором, для которого плотность распределения протонов и нейтронов с точностью до фактора Z/A совпадают, существует довольно большая область на переферии ядра, в которой плотность распределения нейтронов ρ_n существенно больше плотности распределения протонов ρ_p (ρ_n>>ρ_p).Обнаружены также ядра, имеющие протонное гало.
   Нейтронное облако, окружающее кор ядра, простирается на гораздо большие расстояния, чем радиус ядра, определяемый соотношением R = 1.3A^1/3. Так для гало-ядра ¹¹Li пространственное распределение двух нейтронов, образующих ядерное гало вокруг кора ⁹Li, простирается столь далеко, что радиус ядра ¹¹Li оказывается сравним с радиусом ядра ²⁰⁸Pb (см. рис. 6).

20.04.11