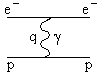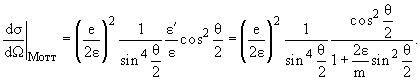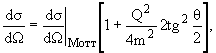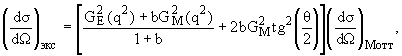Исторически первым указанием на сложную внутреннюю структуру протона и нейтрона явились результаты измерения их магнитных моментов. Измеренные значения магнитных моментов

 μ_p =2.79275_N,
 μ_n = -1.91348_N,
где μ_N = e/(2m_pc) - ядерный магнетон,

отличались от соответствующих предсказаний, ожидавшихся для точечных дираковских частиц -

 μ_p = μ_N,
 μ_n = 0.

    Для исследования структуры нуклона использовались электронные пучки с энергией вплоть до 20 ГэВ. Для изучения распределения заряда и магнитного момента в протоне обычно используют мишени из жидкого водорода и измеряют сечение упругого рассеяния электронов. Т.к. не существует нейтронных мишеней, для исследования нейтронов используют мишени из дейтерия. При этом необходимо отделить эффекты обусловленные протонами. Поэтому нейтронные данные получать труднее и они имеют бОльшие по сравнению с протонами погрешности.

    Пространственные распределения зарядов и токов в протоне исследуют измеряя упругое распределение электронов на протоне. Диаграмма Фейнмана для упругого рассеяния электронов на протоне показана на рис.1.
    Основной механизм реакции - однофотонный обмен, т.к. константа электромагнитного взаимодействия мала (α = 1/137), однофотонный механизм описывает процесс упругого рассеяния с точностью ~1%.
    При однофотонном механизме виртуальный фотон переносит 4-х импульс q

q = p - p' = P - P',

где p ≡ pⁱ = (ε, ) и p' ≡ p' ⁱ = (ε', ') - 4-х импульсы падающего и рассеянного электронов,
P ≡ Pⁱ = (E, ) и P' ≡ P' ⁱ = (E', ') - 4-х импульсы протона в начальном и конечном состоянии.
    Упругое рассеяние означает, что протон остается в основном состоянии. Поэтому переданная энергия и переданный импульс определяются соотношениями

= ε - ε' = E' - E,
= p - ' = ' - P

и передаются нуклону как целому объекту. Квадрат переданного 4-х импульса q² определяется соотношением

q²  =  ² - ² -Q² < 0.

    В случае упругого рассеяния релятивистского электрона на точечной бесспиновой частицы массы m на угол θ энергия ε' и квадрат 4-х импульса рассеянного электрона Q² определяются соотношениями

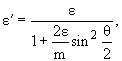
Q² = 4' sin²/2.

Сечение рассеяния определяется формулой Мотта

    Упругое рассеяние электрона на точечной частице со спином 1/2 и  дираковским магнитным моментом описывается соотношением

т.е. магнитное взаимодействие приводит к дополнительному возрастанию сечения под большими углами.
    Нуклон обладает магнитным моментом, отличным от дираковских значений, поэтому формулы (1,2) следует обобщить. Пространственное распределение электрического заряда и магнитного момента в протоне описывается с помощью двух форм-факторов G_E и G_M.
    Упругое рассеяние электронов на нуклоне в этом случае описывается формулой Розенблата.

где

q - четырехимпульс, который электрон передает нуклону, m - масса нуклона, - угол рассеяния электрона, G_E(q²) и G_M(q²) - электрический и магнитный форм-факторы соответственно.
    Для электрических и магнитных форм-фактров получены следующие экспериментальные зависимости от квадрата переданного импульса гамма-кванта.

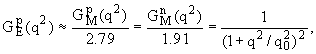
где q₀² = 0.71 ГэВ²/c².
    Если бы протон был точечной частицей, то его электрический форм-фактор имел постоянное значение. Из экспериментов следует, что форм-фактор зависит от переданного импульса как ~1/q⁴, что указывает на конечные размеры протона.
    При нулевом переданном 4-х импульсе

G_E(0) = Q/e (Q - электрический заряд нуклона),
G_M(0) = μ/μ_N (μ - магнитный момент нуклона, μ_N - ядерный магнетон).

    Для протона и нейтрона G_E(0) и G_M(0) имеют следующие значения

(0) = 1,(0) = 0, = 2.79, = -1.91.

    В результате подгонки форм-факторов к экспериментальным данным были получены данные о размерах протона и нейтрона, распределении в них электрического заряда и магнитных моментах
    Для радиусов распределения электрического заряда  и магнитного момента протона получены следующие значения

Радиус распределения магнитного момента нейтрона

Т.е. все три величины в пределах ошибок измерений практически совпадают. Радиус распределения электрического заряда нейтрона

Отличие величины <r²_E>^1/2_n от нуля означает, что заряд нейтрона только после усреднения по всему объему нейтрона равен нулю.

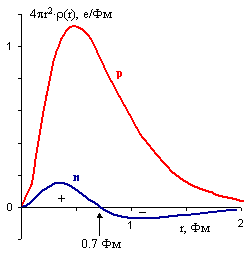
• Протон лишен четкой границы. Плотность заряда в протоне плавно убывает по закону

где ρ(0) = 3 е/Фм³, a = 0.23 Фм.

• Среднее от квадрата радиуса протона

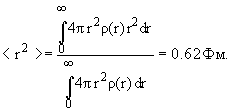
  (5)

• Размер протона соответственно ~0.8 Фм. Размер нейтрона приблизительно такой же.
• В нейтроне центральная часть (r < 0.7 Фм) заряжена положительно, периферийная часть - отрицательно.

Т.е. нейтрон "намагничен" - имеет магнитный момент. Усредненный по объему электрический заряд нейтрона равен нулю.
    Полученные экспериментальные данные по структуре нуклона свидетельствуют о том, что нуклон имеет сложную внутреннюю структуру. По современным представлениям он состоит из кварков, взаимодействующих посредством обмена квантами сильного взаимодействия - глюонами.
    Форм-факторы других адронов  π, K, нельзя измерить непосредственно. Их извлекают из более сложного анализа сечений упругого рассеяния электронов, нуклонов и π-мезонов на нуклоне. Из этих данных следует, что адроны не являются точечными частицами, их размеры сравнимы с размерами нуклона.
    В частности данные по распределению электрического заряда π и K-мезонов получены из анализа углового распределения электронов, образующихся при рассеянии π и K-мезонов на атомах водорода. В случае π и K-мезонов магнитный формфактор равен нулю, т.к. у этих частиц нулевые спины. Q² зависимость электрического формфактора имеет вид

G_E(Q²) = (1 + Q²/a²ћ²)^-1,
a² = 6/<r²>.

    Отсюда

<r²>_π = 0.44 + 0.02 Фм²,    (<r²>_π)^1/2 = 0.67 + 0.02 Фм;
<r²>_K = 0.34 + 0.05 Фм²,     (<r²>_K)^1/2 = 0.58 + 0.04 Фм

    Различие в Q² зависимости электрических формфакторов нуклонов и π и K-мезонов определяется их внутренней структурой. Известно, что протон  и нейтрон состоят из трех кварков p(uud) и n(udd), в то время как π и K-мезоны из кварка и антикварка. Различие в радиусах π и K-мезонов определяется массами составляющих их кварков. С увеличением массы кварка радиус взаимодействия уменьшается.

Последнее обновление 22.09.15.