В физике микромира все т.н. “элементарные” частицы делятся
на два класса: фермионы и бозоны. Фермионами называются частицы с
полуцелыми значениями спина, бозонами - частицы с целыми значениями спина.
Спином называется минимальное значение момента количества движения, которое
может иметь частица. Спины и другие моменты импульсов измеряются в единицах ![]() .
Для частиц с ненулевой массой покоя спин равен моменту импульса частицы в
системе координат, связанной с ней самой. (Значение J спина частиц, указываемое
в таблицах, представляет собой максимальное значение проекции вектора момента
количества движения на выделенную ось, деленное на
.
Для частиц с ненулевой массой покоя спин равен моменту импульса частицы в
системе координат, связанной с ней самой. (Значение J спина частиц, указываемое
в таблицах, представляет собой максимальное значение проекции вектора момента
количества движения на выделенную ось, деленное на ![]() ).
).
Фундаментальными называют частицы, которые по современным
представлениям не имеют внутренней структуры. В природе существует 12
фундаментальных фермионов (со спином 1/2 в единицах ![]() )
)
Табл.5.1
Фундаментальные фермионы |
|||||||
|---|---|---|---|---|---|---|---|
| Взаимодействия | Поколения |
Заряд Q/e |
|||||
1 |
2 |
3 |
|||||
| лептоны | νе | νμ | ντ | 0 | |||
| e | μ | τ | -1 | ||||
| кварки | u | c | t | +2/3 | |||
| d | s | b | -1/3 | ||||
12 фундаментальным фермионам соответствуют 12 антифермионов.
Взаимодействие фундаментальных фермионов осуществляется за
счет 4 типов взаимодействий: гравитационного, сильного, электромагнитного и
слабого. ( см. таблицу 1.1. Введения) Гравитационные силы практически не
проявляются в физике частиц, например, интенсивность гравитационного
взаимодействия двух протонов составляет не более 10-38 интенсивности
их электромагнитного взаимодействия. Взаимодействия
фундаментальных фермионов осуществляются за счет обмена бозонами - квантами
полей.
Сильное взаимодействие осуществляется обменом 8 “цветными”
глюонами
- нейтральными безмассовыми переносчиками сильного взаимодействия.
Электромагнитное взаимодействие
реализуется путем обмена квантами электромагнитного
поля, т.е. гамма-квантами.
![]() -кванты
имеют нулевую массу. Электромагнитным взаимодействиям подчиняются
фундаментальные частицы, занимающие последние три строки в таблице 1, т.е.
заряженные лептоны и кварки. Поскольку кварки в свободном состоянии не
наблюдаются, а входят в состав адронов, т.е. барионов и мезонов, все адроны
подчиняются электромагнитным взаимодействиям.
-кванты
имеют нулевую массу. Электромагнитным взаимодействиям подчиняются
фундаментальные частицы, занимающие последние три строки в таблице 1, т.е.
заряженные лептоны и кварки. Поскольку кварки в свободном состоянии не
наблюдаются, а входят в состав адронов, т.е. барионов и мезонов, все адроны
подчиняются электромагнитным взаимодействиям.
Слабое взаимодействие ( в котором принимают участие все
лептоны и все кварки) переносится массивными W и Z
бозонами. Существуют как положительные W+
бозоны, так и отрицательные W-; Z -бозоны электрически
нейтральны. Массы W и Z бозонов велики - выше 80 ГэВ/с2, следствием
больших масс промежуточных бозонов слабого взаимодействия является малая - по
сравнению с электромагнитной константой - константа слабого взаимодействия.
Глюоны, гамма-квант, W и Z бозоны являются
фундаментальными бозонами. Спины фундаментальных бозонов равны 1.
Таким образом, (без учета античастиц) экспериментально установлено
существование 12 фундаментальных фермионов и 4 фундаментальных бозонов.
Разделение таблицы 5.1 на поколения
оправдано тем фактом, что окружающий нас мир практически полностью построен из
частиц т.н. первого поколения (наименее массивных). Частицы второго и,
тем более, третьего поколений могут быть обнаружены только при высоких энергиях
взаимодействия. Например, t-кварк открыт на ускорителе-коллайдере FNAL, при
столкновении протонов и антипротонов с энергиями 1000 ГэВ.
Первые две строки в таблице 5.1 занимают
лептоны - фермионы, не принимающие участия в сильных взаимодействиях.
Лептонами являются электрически нейтральные нейтрино(и антинейтрино) трех типов
- частицы с массами, много меньшими, чем масса электрона. Нейтрино участвуют
лишь в слабых взаимодействиях. Вторую строку занимают электрон, мюон и
таон - заряженные бесструктурные частицы, участвующие как в слабом, так и
электромагнитном взаимодействиях.
Третья и четвертая строки содержат 6 кварков
(q) - бесструктурных частиц с дробными значениями электрического заряда.
В свободном состоянии эти частицы не наблюдаются, они входят в состав
наблюдаемых частиц - адронов.
Частицы, принимающие участие в сильных взаимодействиях,
называются адронами
(hadrons). Все адроны делятся на два класса: барионы и мезоны.
Барионы
имеют полуцелый спин (т.е. являются фермионами и подчиняются принципу Паули).
Мезоны
- частицы с целым значением спина. Спином частицы (собственным моментом
количества движения частицы) называется величина, измеряемая в единицах ![]() и численно равная максимальному значению проекции собственного момента
количества движения на ось.
и численно равная максимальному значению проекции собственного момента
количества движения на ось.
Все адроны - частицы, имеющие внутреннюю структуру. Они
состоят из кварков (q) и антикварков. Структура барионов (qqq), мезонов -
(q![]() ).
Спины всех кварков равны 1/2.
).
Спины всех кварков равны 1/2.
Квантовые числа кварков перечислены в таблице 5.2 ( В таблице
даны английские термины, обозначающие тип кварков и некоторые из их квантовых
чисел, общепринятые в научной литературе)
Табл.5.2
Квантовые числа кварков |
||||||
|---|---|---|---|---|---|---|
| Квантовое число |
F l a v o r |
|||||
| u | d | c | s | t | b | |
| Q | +2/3 | -1/3 | +2/3 | -1/3 | +2/3 | -1/3 |
| I3 | +1/2 | -1/2 | 0 | 0 | 0 | 0 |
| c (charm) | 0 | 0 | +1 | 0 | 0 | 0 |
| s (strangeness) | 0 | 0 | 0 | -1 | 0 | 0 |
| t (topness) | 0 | 0 | 0 | 0 | +1 | 0 |
| b (bottomness) | 0 | 0 | 0 | 0 | 0 | -1 |
Кроме перечисленных квантовых чисел, кваркам приписывается
еще одно - барионный заряд. Поскольку у всех барионов величина барионного заряда
равно +1, барионный заряд кварков равен 1/3. Структуры из трех кварков (qqq) -
барионы
- имеют полуцелый спин и барионный заряд B = 1. К числу барионов относятся
протон и нейтрон с кварковыми структурами p = (uud), n = (udd).
Антикварки имеют то же значение
спина, что и кварки (т.е. 1/3). Все другие квантовые числа антикварков равны по
абсолютной величине и противоположны по знаку квантовым числам кварков.
Например, структура протона p = (uud), а антипротона ![]() = (
= (![]()
![]()
![]() ).
Его электрический заряд поэтому равен -2/3- 2/3 +1/3= -1, а барионный заряд B(
).
Его электрический заряд поэтому равен -2/3- 2/3 +1/3= -1, а барионный заряд B(![]() )
= -1/3 -1/3 -1/3 = -1.
)
= -1/3 -1/3 -1/3 = -1.
Частицы, состоящие из кварка и антикварка, называются
мезонами, их барионный заряд B = 0. Явления природы, проявляющиеся при невысоких
энергиях частиц, могут быть практически полностью объяснены взаимодействием
фундаментальных частиц 1-го поколения. 2-е поколение фундаментальных частиц
проявляется при более высоких энергиях: первые барионы и мезоны, содержащие
наиболее легкий кварк этого поколения - s-кварк были обнаружены в 60-е годы в
экспериментах на ускорителях. Это т.н. "странные" частицы. Исследование 3-го
поколения фундаментальных частиц возможно только на ускорителях высоких энергий.
Тип кварка (u,d,s,c,b,t) принято называть его
ароматом (flavor). Помимо
перечисленных в таблицах 5.1 и 5.2 характеристик, кварки обладают еще одним
квантовым числом, называемым "цвет"
(color). Каждый из 6 ароматов кварков (u,d,c,s,b,t)
существует в трех цветовых разновидностях: желтой, синей или красной. Антикварки
несут соответствующие цветовые антизаряды: антижелтый, антисиний, антикрасный.
Адроны бесцветны, цвета составляющих их кварков в сумме дают отсутствие цвета
("белый" цвет). Переносчики сильного взаимодействия -глюоны- имеют не один, а
два цветовых индекса- они связывают между собой “цветные”кварки. Всего имеется
не 9, а 8 цветных глюонов, поскольку комбинация жж + сс + кк не имеет цветового
заряда (т.е. является "белой"). Свободные кварки и глюоны не существуют: они
"заперты" внутри бесцветных адронов.
5.2. Законы сохранения и взаимодействия
Все процессы взаимодействия частиц подчиняются законам сохранения. В таблице 2 перечислены законы сохранения и указано, в каком типе фундаментальных взаимодействий данная характеристика сохраняется. Отметим, что некоторые законы сохранения аддитивны /A/ (т.е. в процессе сохраняется суммарная величина - например, во всех взаимодействиях сохраняется сумма энергий частиц). Ряд законов сохранения имеет мультипликативный характер /M/- сохраняется произведение величин. Очень важно, что законы сохранения имеют глубокую связь со свойствами симметрии.
Таблица 5.3
| Характеристика | Символ | Сильное взаимодейст. |
Эл. магн. взаимод. |
Слабое взаимод. |
A или M |
|---|---|---|---|---|---|
| Энергия | E | + | + | + | A |
| Импульс | + | + | + | A | |
| Момент | + | + | + | A | |
| Эл.заряд | Q | + | + | + | A |
| Барионный заряд | B | + | + | + | A |
| Лептонные заряд | Le,Lμ,Lτ | + | + | + | A |
| Странность | s | + | + | - | A |
| Charm | с | + | + | - | A |
| Bottomness | b | + | + | - | A |
| Topness | t | + | + | - | A |
| Изоспин | I | + | - | - | A |
| Р-четность | P | + | + | - | M |
| С-четность | C | + | + | - | M |
| CP-четность | CP or PC | + | + | - | M |
| CPT-четность | CPT | + | + | + | M |
| T-четность | T | + | + | - | M |
В физике высоких энергий часто используется т.н. " естественная" система
единиц , в которой ![]() = c = 1.
= c = 1.![]() c, которая равна
c, которая равна ![]() c = 197 МэВ.Фм.
c = 197 МэВ.Фм.
В системе, где ![]() = c = 1,
= c = 1, ![]() c = 1
и 1 Фм-1 = 0.197 ГэВ.
c = 1
и 1 Фм-1 = 0.197 ГэВ.
Как следует из таблицы 5.3, в сильных взаимодействиях
выполняются все законы сохранения.
Перечисленные в таблице 5.3 законы сохранения для всех
реакций сильного
взаимодействия выполняются без исключений. (
Это одновременно означает наибольшую, по сравнению с другими взаимодействиями,
степень симметрий
этих взаимодействий). Анализ законов сохранения позволяет идентифицировать
неизвестную частицу, если ее рождение происходит в реакции сильного
взаимодействия.
| Задача 5.1. Идентифицировать частицу X
в реакции сильного взаимодействия: p + p |
В реакциях сильного взаимодействия выполняются все законы сохранения.
Определим характеристики частицы X:
Из закона сохранения заряда Q:
Q: +1+1 = +1 + Q(X) + 1 .Отсюда Q(X) = 0.
Закон сохранения барионного заряда:
B: +1+1 = +1 + B(X) + 0, т.е. B(X) = +1.
Закон сохранения странности:
S: 0 + 0 = S(X) +1, т.е. S(X) = -1.
Искомая частица - незаряженный барион с отрицательной странностью. Из таблицы
частиц следует, что этому условию удовлетворяют две частицы ![]() ,
, ![]() 0.
Кварковая структура обеих частиц (uds). Спин обеих частиц 1/2, барионный заряд
равен 1. Отличие их структуры - в разных изоспинах.
0.
Кварковая структура обеих частиц (uds). Спин обеих частиц 1/2, барионный заряд
равен 1. Отличие их структуры - в разных изоспинах.
![]() гиперон имеет изоспин 0, а нейтральный
гиперон имеет изоспин 0, а нейтральный ![]() 0
гиперон принадлежит к группе трех
0
гиперон принадлежит к группе трех ![]() гиперонов с
изоспином 1. Проекции изоспина у членов этой тройки ( изоспинового триплета)
составляют -1, 0 и +1. Нейтральный
гиперонов с
изоспином 1. Проекции изоспина у членов этой тройки ( изоспинового триплета)
составляют -1, 0 и +1. Нейтральный ![]() 0
гиперон - центральный член триплета с проекцией изоспина 0.
0
гиперон - центральный член триплета с проекцией изоспина 0.
Напомним правила сложения квантовых
векторов
Как момент количества движения, так и изоспин частиц являются
квантовыми векторами. Необходимо усвоить правила сложения таких векторов:
![]() +
+ ![]() =
= ![]() ; |
; |![]() |
= C = A + B, A + B - 1, A + B - 2, ..., |A - B|.
|
= C = A + B, A + B - 1, A + B - 2, ..., |A - B|.
Число возможных значений суммарного вектора равно 2D + 1, где D - наименьший из суммируемых векторов.
| Задача 5.2. Определить минимальное
(т.е. пороговое) значение кинетической энергии пиона в системе покоя протона
в реакции
|
Полученные выше формулы для пороговых значений энергии налетающей частицы универсальны. В данной реакции:
Ta = ![]() (1193
+ 494 - 938 - 140)(1193 + 494 + 938 + 140) МэВ = 900 МэВ.
(1193
+ 494 - 938 - 140)(1193 + 494 + 938 + 140) МэВ = 900 МэВ.
| Задача 5.3. Проверить выполнение дискретных законов сохранения той же реакции. |
Закон сохранения эл.заряда Q: -1+1= -1+1.
Закон сохранения барионного заряда В: 0+1 = 1+0.
Закон сохранения странности: 0+0 = -1+1.
Закон сохранения изоспина: ![]() +
+ ![]() =
= ![]() +
+ ![]() .
.
| Задача 5.4. Построить кварковую
диаграмму реакции
|
Процессы сильных взаимодействий часто изображают с помощью
кварковых диаграмм.
Линии кварков (фермионов) не прерываются. Взаимодействие
кварков осуществляется путем обмена глюонами, которые на кварковых диаграммах,
как правило, не указывают. В данном процессе происходит аннигиляция пары u![]() и рождение пары
кварк-антикварк s
и рождение пары
кварк-антикварк s![]() .
.
При использовании закона сохранения полного момента
количества движения
в замкнутой системе необходимо учитывать, что частицы, помимо спинов, обладают
также орбитальными моментами количества движения. В отличие от спинов,
орбитальные моменты могут принимать только целые значения в
единицах ![]() .
.
Cуммарный векторный момент количества движения (момент
импульса) двух частиц складывается из их спинов и орбитальных моментов. Обычно
указывают суммарный орбитальный момент этой пары относительно их общего центра
инерции.
| Задача 5.5.
Проанализировать закон сохранения момента количества движения в реакции
|
Спин ![]() мезонов равен 0. Спин протона 1/2. Спин
мезонов равен 0. Спин протона 1/2. Спин ![]() ++ резонанса 3/2.
++ резонанса 3/2.
Определим суммарный орбитальный момент протона и пи-мезона в системе центра
инерции:
0 + ![]() +
+ ![]() =
= ![]()
![]()
![]() =
= ![]() ,
, ![]() .
.
Таким образом, из закона сохранения момента количества движения нельзя сделать однозначного вывода об орбитальном моменте системы пион-нуклон в данной реакции. Но этот вывод можно сделать, если учесть еще один закон сохранения, выполняющийся в сильных и электромагнитных взаимодействиях:
Закон сохранения пространственной четности(См. Раздел 2). При условии сохранения пространственной, или Р-четности,
волновая функция частицы (или системы частиц) может иметь собственные значения
оператора Р-четности, равные либо р = +1, либо р = -1.
Все адроны имеют собственную
четность (см. таблицу адронов) в собственной системе координат.
Р-четность нуклона р = +1, Р- четность пионов р = -1. Помимо собственной
четности частицы, при использовании закона сохранения четности необходимо
учесть, что четность волновой функции системы частиц равна произведению их
собственных четностей на четность, соответствующую их орбитальному
движению. Эта четность равна (-1)L, где L- орбитальный
момент частиц.
Возвратимся к решению задачи 5.5 о рождении ![]() ++резонанса.
Применим теперь закон сохранения пространственной четности (мультипликативный
закон сохранения - т.е. в сильных и электромагнитных взаимодействиях
сохраняется произведение пространственных четностей):
++резонанса.
Применим теперь закон сохранения пространственной четности (мультипликативный
закон сохранения - т.е. в сильных и электромагнитных взаимодействиях
сохраняется произведение пространственных четностей):
Четность ![]() -резонансов
равна р = +1. Четность системы пион-нуклон равна
-резонансов
равна р = +1. Четность системы пион-нуклон равна
(+1)(-1)(-1)L = +1 ![]() (-1)L = -1.
(-1)L = -1.
Таким образом, из двух возможных ( по закону сохранения момента импульса) значений L закону сохранения Р-четности удовлетворяет только L = 1. Реакция идет при орбитальном моменте системы пион-нуклон, равном 1 ( т.е. в Р-канале). Напомним, что физике микромира значения орбитальных моментов часто обозначают буквами латинского алфавита:
L |
0 |
1 |
2 |
3 |
4 |
S |
P |
D |
F |
G |
В квантовой теории существует удобный метод описания и
расчета процессов взаимодействия частиц, основанный на использовании
диаграмм Фейнмана
(ДФ).
В диаграммах Фейнмана физическому процессу сопоставляется его
графическая схема. Каждой участвующей в процессе частице соответствует линия.
Обычно линии фермионов - тонкие прямые линии. Линии бозонов изображают либо
волнистыми, либо штриховыми прямыми. (Частицам, не являющимся по современным
представления бесструктурными, иногда сопоставляются на диаграммах либо толстые
линии, либо пучки параллельных линий).
Диаграмма Фейнмана (ДФ) задает алгоритм вычисления амплитуды
вероятности процесса. Каждому элементу диаграммы соответствуют определенные
множители в расчете амплитуды вероятности. Линии, один из концов которых
свободен, соответствуют свободным частицам. В расчете амплитуды вероятности этим
линиям отвечают волновые функции частиц. Квадрат модуля амплитуды вероятности
определяет вероятность процесса
Линии на ДФ могут описывать распространение как частиц, так и
античастиц: направление стрелок на линиях античастиц противоположно направлениям
стрелок на линиях частиц.
Взаимодействие частиц на диаграмме изображается вершиной (или
узлом), в котором сходятся две фермионных и одна бозонная линии. Каждой вершине
в амплитуде вероятности процесса соответствует константа взаимодействия. В
случае электромагнитных процессов вершинной константой является заряд
(![]() e)1/2
= e/(
e)1/2
= e/(![]() c)1/2. В
системе единиц
c)1/2. В
системе единиц ![]() = c = 1
= c = 1 ![]() (
(![]() e)1/2
= e. Величина квадрата этой константы при не очень высоких энергиях равна
e)1/2
= e. Величина квадрата этой константы при не очень высоких энергиях равна
|
(5.1) |
Частицы, изображенные линиями, начинающимися и кончающимися в вершинах - это
т.н. виртуальные частицы. Линиям
виртуальных частиц в расчете ДФ сопоставляются функции распространения этих
частиц, называемые пропагаторами. Именно виртуальные частицы
ответственны за реализацию взаимодействия частиц. Для процессов взаимодействия,
которые и осуществляются путем рождения и поглощения виртуальных частиц,
характерно, что в течение интервала времени взаимодействия ![]() t
имеет место отклонение
t
имеет место отклонение ![]() E энергии виртуальной частицы от ее точного
значения, соответствующего закону сохранения, причем
E энергии виртуальной частицы от ее точного
значения, соответствующего закону сохранения, причем
|
(5.2) |
(соотношение неопределенности Гейзенберга для энергии и времени)
Для виртуальных частиц
E2 |
(5.3) |
Следует подчеркнуть, что в целом для всего процесса законы сохранения
выполняются точно, в частности, полная энергия частиц до взаимодействия равна
полной энергии частиц после взаимодействия.
На рис. 5.1 изображена диаграмма Фейнмана для рассеяния
фотона на электроне. (Вектор времени направлен слева направо). Перемена
направлений на фермионной линии дает диаграмму Фейнмана для рассеяния фотона на
позитроне. Диаграммы Фейнмана обладают замечательными топологическими
свойствами: если на рис.1 направить вектор времени снизу вверх
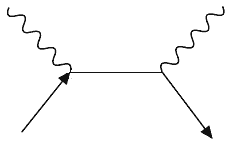
Рис.5.1
(или, сохраняя направление вектора времени, повернуть ее на 900),
диаграмма будет изображать двухфотонную аннигиляцию ![]()
![]() +
+ ![]() .
.
Диаграммы Фейнмана не только являются иллюстрацией реакций с
частицами, но и позволяют - даже без проведения точного расчета - сделать
некоторые важные оценки соотношения вероятностей процессов. Например, с их
помощью легко доказать доминирующую роль низших по числу вершин (или количеству
виртуальных частиц) диаграмм в электромагнитных взаимодействиях.
Рассмотрим в качестве примера рассеяние электрона на
электроне. Квантом электромагнитного взаимодействия является виртуальный фотон.
На рисунке 5.2 показана обобщенная диаграмма этого процесса,
которая может быть представлена как сумма диаграмм с разным количеством
вершин.
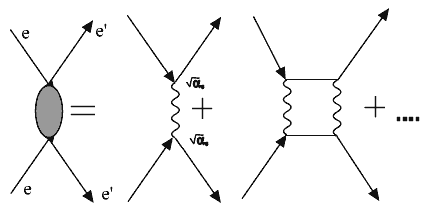
Рис.5.2
Поскольку взаимодействие электромагнитное, каждой вершине соответствует константа электромагнитного взаимодействия
( |
(5.4) |
Первая из диаграмм Фейнмана, дающая вклад в процесс
рассеяния электрона на электроне, имеет две вершины, ее вклад в амплитуду
вероятности процесса (матричный элемент процесса M) пропорционален произведению
квадрату константы (5.4): M ~ ![]() e.
e.
Вероятность процесса (эффективное сечение) пропорциональна
квадрату матричного элемента ![]() ~ M2. Поэтому вклад первой из диаграмм в правой части рис.5.2 в
вероятность рассеяния пропорционален величине
~ M2. Поэтому вклад первой из диаграмм в правой части рис.5.2 в
вероятность рассеяния пропорционален величине ![]() 2
2 ![]() (1/137)2.
Вклады диаграмм более высокого порядка, т.е. с большим числом вершин, много
меньше вклада этой первой диаграммы. Например, вторая из диаграмм Фейнмана в
правой части рис.5.2, дает в вероятность процесса рассеяния электрона на
электроне вклад, пропорциональный
(1/137)2.
Вклады диаграмм более высокого порядка, т.е. с большим числом вершин, много
меньше вклада этой первой диаграммы. Например, вторая из диаграмм Фейнмана в
правой части рис.5.2, дает в вероятность процесса рассеяния электрона на
электроне вклад, пропорциональный ![]() 4
4
![]() (1/137)4.
(Следует отметить, что “константы взаимодействия”, строго говоря,
не постоянны: они зависят от энергии взаимодействия. Однако в области
энергий взаимодействия E<10 ГэВ этим эффектом можно пренебречь)
(1/137)4.
(Следует отметить, что “константы взаимодействия”, строго говоря,
не постоянны: они зависят от энергии взаимодействия. Однако в области
энергий взаимодействия E<10 ГэВ этим эффектом можно пренебречь)
| Задача 5.6. Оценить отношение вероятностей процессов трехфотонной и двухфотонной аннигиляции пары электрон-позитрон. |
Процессы e+ + e-![]()
![]() +
+ ![]() и e+ + e-
и e+ + e-![]()
![]() +
+ ![]() +
+ ![]() в низшем порядке по константе электромагнитного взаимодействия могут быть
представлены ДФ на рис.5.3.
в низшем порядке по константе электромагнитного взаимодействия могут быть
представлены ДФ на рис.5.3.
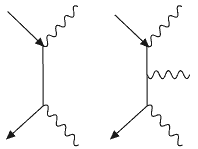
Рис.5.3
Для первого процесса с двумя вершинами вероятностьW1 ~ ![]() 2,
для второго W2 ~
2,
для второго W2 ~ ![]() 3.
Отношение вероятностей (W1/W2) ~ 137. Отметим, что первая
диаграмма соответствует распаду парапозитрония, т.е. состояния системы e+e-
с полным моментом количества движения J = 0 ( спины e+ и e-
антипараллельны). Вторая диаграмма отражает распад ортопозитрония - системы e+e-
с полным моментом количества движения J = 1.
3.
Отношение вероятностей (W1/W2) ~ 137. Отметим, что первая
диаграмма соответствует распаду парапозитрония, т.е. состояния системы e+e-
с полным моментом количества движения J = 0 ( спины e+ и e-
антипараллельны). Вторая диаграмма отражает распад ортопозитрония - системы e+e-
с полным моментом количества движения J = 1.
Техника расчетов эффективных сечений процессов с помощью
диаграмм Фейнмана была в 50-х годах XX века развита для электромагнитных
взаимодействий. Построенная на этой основе квантовая электродинамика (КЭД)
является наиболее последовательной и точной физической теорией. Однако
основополагающая идея о том, что взаимодействие частиц микромира осуществляется
путем обмена промежуточным бозоном - квантом данного поля, является
универсальной. В 60-е годы XX века на этой идее была построена теория слабых
взаимодействий частиц (Глэшоу,
Вайнберг,
Салам), объединяющая
электромагнитные и слабые взаимодействия в единую теорию электрослабых
взаимодействий. Экспериментальное обнаружение (К. Руббиа,1983) промежуточных бозонов W+,
W- и Z0, реализующих слабое взаимодействие,
явилось блестящим доказательством обменной теории слабых взаимодействий.