Использование константы конверсии в курсе
"Физика ядра и частиц"
"Физика ядра и частиц" представляет собой завершающий этап
курса общей физики в программе Московского государственного университета им.
M.В. Ломоносова. Одной из трудностей, с которыми сталкивается преподавание этого
раздела общей физики на третьем курсе физического факультета, является
необходимость освоения методов расчета с использованием принятых в субатомной
физике единиц измерения физических величин.
Переход от освоенных студентами за 2 года обучения систем СИ
и СГС к внесистемным единицам физики микромира значительно упрощается при
использовании в процессе решения задач т.н. константы конверсии ћc ("conversion
constant") [1]. Использование константы конверсии позволяет за
счет упрощения решения задачи уделить больше внимания ее физическому содержанию.
В субатомной физике основной единицей измерения энергии
является 1 МэВ:
1 МэВ = 106 эВ = 10-3 ГэВ = 10-6 ТэВ = 1.60218.10-13 Дж.
Линейные размеры субатомных объектов определяют, как правило, в единицах
Ферми:
1 Фм =10-13 см.
Константа конверсии равна:
ћc = 197.327 МэВ·Фм ≈ 200 МэВ·Фм =2·10-11МэВ·см.
Рассмотрим примеры решения задач курса субатомной физики с использованием
константы конверсии.
Задача 1. Определить полную E и кинетическую энергию T
электрона, приведенная длина волны которого равна 10–2 Фм.
Приведенная длина волны частицы выражается как:

откуда
 = 2·104 МэВ = 20 ГэВ. = 2·104 МэВ = 20 ГэВ.
Поскольку энергия покоя электрона mc2
всего 0.511 МэВ, то при таких высоких энергиях его полная и кинетическая энергии
практически совпадают ( их разность при условиях задачи меньше 0.1%.) Поэтому
окончательный ответ имеет вид:
E ≈ T ≈ 20 ГэВ.
Энергии электронов 20 ГэВ и выше достижимы в настоящее время на ряде
электронных ускорителей высоких энергий. Например, на ускорителе LEP в
Европейском центре ядерных исследований (CERN) энергии электронов и позитронов,
движущихся навстречу друг другу в этом ускорителе на встречных пучках,
составляла около 100 Гэв.
Задача 2. Оценить расстояние максимального сближения  -частицы и ядра золота при бомбардировки мишени
из золота пучком -частицы и ядра золота при бомбардировки мишени
из золота пучком  -частиц с
кинетическими энергиями 22 МэВ. Сравнить результат с суммой радиусов ядер золота
и гелия. -частиц с
кинетическими энергиями 22 МэВ. Сравнить результат с суммой радиусов ядер золота
и гелия.
При лобовом соударении налетающей частицы и ядра золота
кинетическая энергия Т  -частицы целиком
тратится на преодоление потенциального кулоновского барьера : -частицы целиком
тратится на преодоление потенциального кулоновского барьера :
 , ,  = 10.4 Фм, = 10.4 Фм,
RHe + RAu = r0(41/3 +1971/3) ≈
10 Фм.
При кинетических энергиях α-частиц 22 МэВ и выше расстояние наибольшего
сближения ядер гелия и золота начинает быть сравнимым с размерами ядерных
систем. Это означает, что чисто кулоновское рассеяние, отраженное знаменитой
формулой Резерфорда, не исчерпывает взаимодействие нуклонов. При больших
энергиях в формулу Резерфорда вводят еще один множитель - форм-фактор,
отражающий размеры и внутреннюю структуру сталкивающихся нуклонов. Результат
решения данной задачи показывает, что введение форм-фактора необходимо при
кинетических энергиях  -частицы,
превышающих 22 МэВ. -частицы,
превышающих 22 МэВ.
В данном примере умножение и деление на константу конверсии
позволяет избежать введения явного вида квадрата единичного заряда, используя
вместо него хорошо известную величину – постоянную тонкой структуры е2/ћc
= 1/137.
Задача 3. Вероятность β-распада нестабильных ядер зависит, в
первую очередь, от орбитального момента, уносимого лептонами, вылетающими при
распаде. Например, при распаде ядра 60Co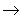 60Ni
+ e- + 60Ni
+ e- + 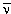 e
энергетически возможны три канала β-распада: на основное состояние
ядра-продукта, первое и второе возбужденные состояния. Эти три состояния никеля
имеют, соответственно, значения спинов 0, 2, 4 и положительные четности.
Основное состояние 60Со имеет спин и четность 5+ [2].
Показать, что β-распад с наибольшей вероятностью будет происходить на второй
возбужденный уровень (4+) ядра никеля. e
энергетически возможны три канала β-распада: на основное состояние
ядра-продукта, первое и второе возбужденные состояния. Эти три состояния никеля
имеют, соответственно, значения спинов 0, 2, 4 и положительные четности.
Основное состояние 60Со имеет спин и четность 5+ [2].
Показать, что β-распад с наибольшей вероятностью будет происходить на второй
возбужденный уровень (4+) ядра никеля.
Применение закона сохранения момента количества движения к
трем возможным каналам распада кобальта показывает, что только при β-распаде
на возбужденный уровень со спином 4 орбитальный момент, уносимый электроном и
нейтрино, может быть равен нулю. Это т.н. "разрешенный" переход. Он
осуществляется почти со 100% вероятностью, хотя энергетически – из трех
возможных переходов - он наименее выгоден. Хотя прямое доказательство того
факта, что β-распад с нулевым значением орбитального момента лептонов должен
иметь наибольшую вероятность, осуществляется лишь методами квантовой теории
поля, помочь в понимании этого явления может "классическая" оценка максимального
значения орбитального момента лептонов распада. Одновременно эта оценка служит
интересной иллюстрацией соотношения классической и квантовой теорий. С
классической точки зрения, максимальное значение орбитального момента лептонов
распада равно l = Rpmax, где R - радиус ядра (например с
А = 60) , а pmax - максимальное значение импульса суммы лептонов. В
пределе, когда максимальная кинетическая энергия распада T уносится
антинейтрино, T = pmaxc. Тогда максимальный орбитальный момент (в
единицах ћ) оказывается равным
 << 1 .
<< 1 .
Таким образом, в "классическом" пределе вылет лептонов с ненулевым
орбитальным моментом вообще невозможен, "запрещен". Квантовый, т.е. реальный,
мир имеет гораздо больше возможностей, но в нем с наибольшей вероятностью
происходят именно те события, которые "разрешены" классической физикой.
Задача 4 .При изучении вращательных спектров атомных ядер (см.
некоторые примеры таких спектров в [2]) нетрудно
оценить момент инерции вращающегося ядра. Рассмотрим, например, вращательный
спектр ядра 170Hf. В таблице даны значения спинов уровней
вращательной "полосы", энергии этих уровней и интервалы энергий ΔE
между данным уровнем и низшим по энергии. Соотношение энергий уровней
вращательной полосы, спинов уровней и соответствующих этим состояниям моментов
инерции ядра даны нижеследующими формулами:
 . .
Таблица. Спины, энергии, интервалы энергий и моменты инерции
состояний вращательной полосы ядра 170Hf.
J |
2 |
4 |
6 |
8 |
10 |
E, МэВ |
0.100 |
0.321 |
0.641 |
1.041 |
1.503 |
ΔЕ,
МэВ |
0.100 |
0.221 |
0.320 |
0.400 |
0.462 |

|
60.0 |
63.3 |
68.7 |
75.0 |
82.3 |
Обычно в физике ядра рассчитывают не момент инерции ядра в
том или ином состоянии, а величину  = 2I/ћ2 в единицах МэВ–1. Результаты расчета этой величины
для пяти возбужденных состояний ядра 170Hf приведены в четвертой
строке таблицы.
= 2I/ћ2 в единицах МэВ–1. Результаты расчета этой величины
для пяти возбужденных состояний ядра 170Hf приведены в четвертой
строке таблицы.
Расчет показывает, что момент инерции ядра растет с
увеличением момента количества движения и, соответственно, угловой частоты
вращения. Этот результат хорошо понятен на основе капельной модели ядра. Важным
и интересным фактом, который можно легко продемонстрировать студентам на этом
примере, является то, что полученные в расчете моменты инерции как минимум вдвое
меньше, чем момент инерции твердотельного ротатора с такой же массой. Нижний
предел величины  ,
пропорциональной моменту инерции, можно получить по формуле момента инерции
сферы радиуса R (здесь снова удобно использовать константу конверсии): ,
пропорциональной моменту инерции, можно получить по формуле момента инерции
сферы радиуса R (здесь снова удобно использовать константу конверсии):

Таким образом, проведенный несложный расчет доказывает,
что ядро в низших возбужденных состояниях имеет значения момента инерции,
составляющие не более 50% момента инерции твердого ротатора с той же массой.
Часть нуклонов ядра оказывается не участвующей во вращательном движении
вследствие эффекта спаривания нуклонов, приводящего к сверхтекучим
свойствам ядер в основном и низших возбужденных состояниях. Разрыв нуклонных
пар, происходящий при очень высоких моментах вращения ядер, проявляется в
скачкообразном росте момента инерции ядра до величин близких к полученной выше
твердотельной оценке. Этот эффект (т.н. бекбендинг) хорошо изучен в последние 20
лет на ускорителях тяжелых ионов.
Задача 5. Оценить радиус слабых взаимодействий по массе промежуточных
бозонов W, Z.
Процесс слабого распада состоит в испускании и поглощении виртуального
промежуточного бозона. Если Δt − время взаимодействия, а масса бозона
представляет собой неопределенность в энергии ΔE, то из соотношения
неопределенностей следует, что:
 . .
Верхний предел радиуса взаимодействия составляет при этом:

Как следует из приведенных примеров, использование
константы конверсии упрощает ход решения целого ряда стандартных задач
университетского курса "Физика ядра и частиц". Эта же константа помогает в
переходе от обычной системы единиц физики ядра, используемой в данных примерах,
к так называемой "естественной системе" [3], в
которой ћ = c = 1. Эта система единиц широко используется в физике высоких
энергий. В "естественной системе" равна единице и константа конверсии, что
позволяет получить соотношение между единицами длины и энергии:
1 ћc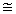 200 МэВ·Фм;
1 Фм-1 200 МэВ·Фм;
1 Фм-1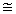 200 МэВ. 200 МэВ.
На ускорителях высоких энергий измеряют характеристики
процессов (например, их эффективные сечения) как функции переданного системе
импульса. Эта величина на графиках дается либо в энергетических единицах (МэВ
или ГэВ), либо в эквивалентных 0.2 ГэВ единицах обратной длины Фм–1.
- Particle Physics. Booklet. Springer,1998, or
http://pdg.lbl.gov/
- Субатомная физика. Под редакцией Б.С.Ишханова. Москва, МГУ, 1994.
- Д. Перкинс. Введение в физику высоких энергий. Москва,
Энергоатомиздат,1991.

|
![]() = 2I/ћ2 в единицах МэВ–1. Результаты расчета этой величины
для пяти возбужденных состояний ядра 170Hf приведены в четвертой
строке таблицы.
= 2I/ћ2 в единицах МэВ–1. Результаты расчета этой величины
для пяти возбужденных состояний ядра 170Hf приведены в четвертой
строке таблицы.![]() ,
пропорциональной моменту инерции, можно получить по формуле момента инерции
сферы радиуса R (здесь снова удобно использовать константу конверсии):
,
пропорциональной моменту инерции, можно получить по формуле момента инерции
сферы радиуса R (здесь снова удобно использовать константу конверсии):![]()
![]() .
.![]()
![]() 200 МэВ·Фм;
1 Фм-1
200 МэВ·Фм;
1 Фм-1![]() 200 МэВ.
200 МэВ.