В § 10.2 мы рассматривали рассеяние при такой
энергии полной системы, когда наряду с упругим возможно и неупругое
рассеяние. Это было отражено в асимптотическом условии (10.7), требующем,
чтобы канальные функции un(r) в неупругих каналах
представляли собой расходящиеся сферические волны. Если же энергия недостаточна
для возбуждения некоторого состояния мишени, то в этом канале асимптотическая
канальная функция un(r) должна иметь вид экспоненциально
затухающей волны.
Сейчас мы рассмотрим случай, когда в задаче двухканального рассеяния
неупругий канал закрыт. Кроме того, предположим, что энергия Е полной
системы близка к энергии одного из собственных состояний дискретного
спектра гамильтониана
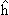 2
неупругого канала. Пусть {φλ} и {Eλ} − собственные
функции и собственные значения гамильтониана
2
неупругого канала. Пусть {φλ} и {Eλ} − собственные
функции и собственные значения гамильтониана
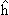 2:
2:
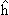 2φλ
= Eλφλ. 2φλ
= Eλφλ. |
(12.1) |
Тогда наше предположение об энергии Е можно записать в виде
В этом случае в спектральном разложении гриновского оператора
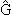 2(E)
можно ограничиться одним членом:
2(E)
можно ограничиться одним членом:
 |
(12.3) |
Подставляя это выражение в (10.17), получаем
u1 =
 (r)
+ [ (r)
+ [ (E)V12φ0] (E)V12φ0] <φ0|V12|u1> <φ0|V12|u1> |
(12.4) |
Это − интегральное уравнение для канальной функции u1(r),
асимптотика которой
u1(r)|r→∞
= eikr + ƒ(k',k) |
(12.5) |
дает амплитуду упругого рассеяния с учетом связи между каналами 1
и 2. Учитывая асимптотику функции
 и функции Грина
и функции Грина
 (E)
(см. (6.20)):
(E)
(см. (6.20)):
 (r)|r→∞
= eikr + ƒ(k',k) (r)|r→∞
= eikr + ƒ(k',k) ,
, |
(12.6) |
 (E,r,r')|r→∞
= − (E,r,r')|r→∞
= − [ [ (r'
)]* (r'
)]* ,
, |
(12.7) |
получаем амплитуду упругого рассеяния в виде суммы двух слагаемых:
| ƒ(k',k) = ƒpot(k',k)
+ Δƒ(k',k), |
(12.8) |
где ƒpot(k',k) − амплитуда потенциального
рассеяния в канале 1, а Δƒ(k',k) − дополнительная
часть амплитуды, обусловленная взаимодействием связанного состояния
в канале 2 с непрерывным спектром в канале 1:
 |
(12.9) |
Чтобы найти эту часть амплитуды, надо решить уравнение (12.4) относительно
канальной функции u1.
Для решения воспользуемся следующим приемом: заменим уравнение
(12.4) двумя связанными уравнениями:
u1 =
 + λ(E)
+ λ(E) (E)V12φ0, (E)V12φ0, |
(12.10) |
 |
(12.11) |
где λ(E) − вспомогательная функция, определяемая соотношением (12.11).
Далее подставим (12.10) в (12.11):
 |
(12.12) |
отсюда находим λ(E):
 |
(12.13) |
здесь мы подставили вместо гриновского оператора
 (E)
его явное выражение (10.16).
(E)
его явное выражение (10.16).
Теперь воспользуемся спектральным представлением этого оператора:
 |
(12.14) |
где
| ρ(k') = ρ(k') =
μћk'/(2πћ)3; E' = ћ2k'2/2μ
. |
(12.15) |
При интегрировании по энергии воспользуемся для обхода полюса известным
приемом:
 |
(12.16) |
или иначе
 |
(12.17) |
где знак
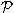 означает,
что интеграл берется в смысле главного значения.
означает,
что интеграл берется в смысле главного значения.
Подставляя (12.14) в (12.13), запишем матричный элемент, входящий
в знаменатель этого выражения, в виде
 |
(12.18) |
где вещественная и мнимая части комплексного числа (12.18) даются
выражениями
 |
(12.19) |
| Г = 2π∫|<ψ1,k'|V12|φ0>|2ρ(k')dΩ
. |
(12.20) |
Таким образом, функция λ(E) быстро меняется с энергией частицы в
окрестности точки (12.2):
 |
(12.21) |
Вместе с λ(E) так же быстро меняется и амплитуда (12.9):
 |
(12.22) |
Дальнейшие вьпсладки проведем для случая, когда
оператор межканального взаимодействия
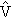 12
связывает состояние φ0 закрытого канала 2 лишь с s-волной
непрерывного спектра в канале 1. Согласно § 3.2, волновые функции
12
связывает состояние φ0 закрытого канала 2 лишь с s-волной
непрерывного спектра в канале 1. Согласно § 3.2, волновые функции
 и
и
 в этом случае заменяются выражениями
в этом случае заменяются выражениями

 |
(12.23) |
где δ0 = δ0(E) − s-фаза потенциального рассеяния
в канале 1, a ψ1,k(r) − вещественная функция.
Подставляя их в (12.20) и (12.22), получаем
 |
(12.24) |
 |
(12.25) |
Назовем амплитуду Δƒ(k',k) ≡ ƒres
резонансной амплитудой рассеяния
и будем записывать ее в виде
 |
(12.26) |
где
Точку Е = Еr будем называть энергией
резонанса. Как видим, она не совпадает с положением связанного
состояния в закрытом канале. В связи с этим параметр Д будем называть
сдвигом резонанса. Его значение дается формулой (12.19), которая показывает,
что этот сдвиг обусловлен взаимодействием связанного состояния в канале
2 с непрерывным спектром в канале 1.
Полная амплитуда рассеяния (12.8) есть сумма резонансной амплитуды
(12.26) и амплитуды потенциального рассеяния ƒ0(k',k),
которая, в отличие от нее, плавно меняется с энергией в окрестности
резонанса:
| ƒ(k',k) ≡ ƒpot
+ ƒres |
(12.28) |
Вероятность упругого рассеяния есть сумма трех слагаемых
| dσ/dΩ = |ƒpot + ƒres|2
= (dσ/dΩ)pot + (dσ/dΩ)res + (dσ/dΩ)int
; |
(12.29) |
сечение потенциального рассеяния da
| (dσ/dΩ)pot = |ƒpot(k',k)|2
, |
(12.30) |
сечение резонансного рассеяния
 |
(12.31) |
интерференционный член
| (dσ/dΩ)int = 2Re{ƒpot
ƒ*res}. |
(12.32) |
Выражение (12.31) называется
формулой Брейта− Вигнера. Из нее
видно, что сечение резонансного рассеяния достигает максимального значения
в точке Е = Еr и уменьшается вдвое при отклонении от нее
на величину ±1/2Г. Будем называть параметр Г
шириной резонанса. Если Г << Еr,
то максимум в сечении (12.31) симметричен. Резонанс же в полном сечении
(12.29), как правило, всегда асимметричен благодаря интерференционному
слагаемому (12.32).
Мы рассматриваем случай, когда резонанс проявляется только в
s-волне. Поэтому, используя (3.25), выделим в амплитуде потенциального
рассеяния соответствующее слагаемое
 |
(12.33) |
оставив в амплитуде
 pot(k',k)
вклад всех других волн
pot(k',k)
вклад всех других волн
 |
(12.34) |
Тогда полная амплитуда s-рассеяния принимает вид:
 |
(12.35) |
Подставляя (12.33) в (12.32), видим, что в дифференциальном
сечении резонансная амплитуда интерферирует со всеми парциальными амплитудами
потенциального рассеяния. В интегральном же сечении после интегрирования
по углам вылета рассеянной частицы, резонансная амплитуда интерферирует
(в рассматриваемом случае) лишь с s-волновой частью амплитуды потенциального
рассеяния:
 |
(12.36) |
Начиная с формулы (12.23), все дальнейшие конкретные
выражения были получены нами для частного случая, когда состояние φ0
закрытого канала 2 связано лишь с s-волной непрерывного спектра в канале
1. Однако общая структура этих выражений, равно как и общие заключения
о характере интерференции между резонансным и потенциальным рассеяниями,
остаются в силе, когда эта связь касается любой другой волны.
![]() 2
неупругого канала. Пусть {φλ} и {Eλ} − собственные
функции и собственные значения гамильтониана
2
неупругого канала. Пусть {φλ} и {Eλ} − собственные
функции и собственные значения гамильтониана
![]() 2:
2:![]() 2(E)
можно ограничиться одним членом:
2(E)
можно ограничиться одним членом:![]() и функции Грина
и функции Грина
![]() (E)
(см. (6.20)):
(E)
(см. (6.20)):


![]() (E)
его явное выражение (10.16).
(E)
его явное выражение (10.16).![]() означает,
что интеграл берется в смысле главного значения.
означает,
что интеграл берется в смысле главного значения.


![]() 12
связывает состояние φ0 закрытого канала 2 лишь с s-волной
непрерывного спектра в канале 1. Согласно § 3.2, волновые функции
12
связывает состояние φ0 закрытого канала 2 лишь с s-волной
непрерывного спектра в канале 1. Согласно § 3.2, волновые функции
![]() и
и
![]() в этом случае заменяются выражениями
в этом случае заменяются выражениями
![]() pot(k',k)
вклад всех других волн
pot(k',k)
вклад всех других волн









