Радиоактивным распадом будем называть такой процесс, при котором ядро из начального состояния переходит в конечное состояние с меньшей энергией.
    Радиоактивность − частный случай ядерной реакции.
    α-распад − самопроизвольное испускание ядра гелия.

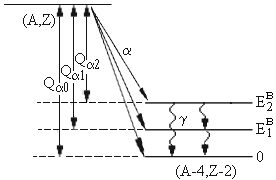Рис. 80. Иллюстрация переходов системы из одного энергетического состояния в другое путем γ-излучения. Eγ = hν ≈ Ei − Ef.

    Ядро (A,Z) может распадаться на конечное ядро (A-4,Z-2) как на его основное состояние состояние, так и на возбужденные. Возбужденные состояния конечного ядра в свою очередь переходят в основное состояние путем испускания γ-квантов (рис. 80). Спектры γ-излучения так же, как и спектры α-частиц, линейчатые.
    Ядра, не испытывающие никаких превращений после того, как они достигли основного состояния, называют стабильными.
    Нестабильные ядра, стремясь к большей стабильности, испускают одну или несколько частиц.
    Такое самопроизвольное превращение возможно только при условии, что масса исходного ядра превышает сумму масс дочернего ядра и α-частицы. При этом энергия распада будет положительной. Такие реакции называют экзотермическими − с выделением энергии.
     Энергия распада на основное состояние дочернего ядра:

Q_α0 = М(A,Z)с² − [M(A-4,Z-2)c² + М(α)с²] > 0.

При распаде на возбужденные состояния конечного ядра энергия распада будет меньше на энергию возбуждения.
Энергия отдачи, которую получает оставшееся ядро R, мала из-за большой массы M(A-4,Z-2):

Q_α = E_α + E_R,  |p_α| = |p_R|  →  E_α М(α) = E_RM(A-4,Z-2).

. Таким образом, кинетическая энергия испускаемых α-частиц близка к Q_α: E_α ≈ Q_α(A-4)/A − эта энергия регистрируется в виде спектральной линии.
    Если происходит распад на возбужденные уровни дочернего ядра, то появляются линейчатые спектры, причем, если испускается α-частица из возбужденного состояния ядра в основное, то ее энергия будет большей, и такие α-частицы называют длиннопробежными.
    α-Распад встречается только у тяжелых ядер с Z > 83 и у ядер с энергией связи на нуклон ε ≤ 7 МэВ, но иногда может быть запрет по спину или четности, если не выполняются законы их сохранения. Тогда распад не происходит или затруднен.
    Если Q > 0, то испускаются α-частицы и возникает линейчатый спектр (рис. 81).
    В 1911 году обнаружили, что электроны при радиоактивном распаде имеют непрерывный спектр (рис. 82).

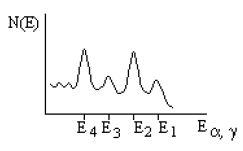Рис. 81. Линейчатый спектр α- или γ-излучения.

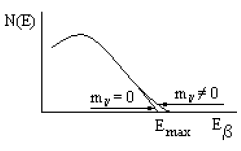Рис. 82. Непрерывный спектр электронов при β-распаде.

    β-Pаспад − испускание электронов (или позитронов) в результате превращения нейтрона или протона в ядре. Теперь установлено, что β-распад есть процесс, в результате которого исходное ядро превращается в ядра с зарядом Z ± 1:

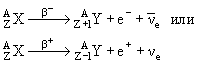
    Ядро X может испытать β-распад только тогда, когда его масса больше, чем сумма масс дочернего ядра Y и электрона:

E_d = {М(Х) - [M(Y) + m_е]}с² > 0.

Таким образом, свободный нейтрон испытывает β-распад

т.к. m_р < m_n, то β⁺-распад свободного протона невозможен, и процесс р → n + e⁺ + ν может происходить только в ядре X, для которого E_d > 0.
    Непрерывный спектр электронов в β-распаде привел Паули к гипотезе о вылете двух частиц, одна из которых − электрон, а другая − нейтральная и не регистрируется при β-распаде, но энергию уносит. Эта частица была названа нейтрино ("нейтрончик"). В зависимости от того, имеет нейтрино массу или его масса равна нулю, спектр электронов вблизи границы Е_maх меняется (см. рис. 82).
     Проблема массы нейтрино не решена до сих пор. Наиболее реальная оценка дает m_νc² < 2 эВ.
    Так как процессы происходят с ядрами в атомах, то можно написать условия β-распада, используя атомные массы M^ат:

M^ат(А,Z)c² = M(A,Z)с² + Zm_ec² − E_L

(E_L − энергия связи электрона в атоме)
    Так как разность энергий связи электронов в начальном (E_L) и конечном атомах (E_L') мала

E_L − E_L' ≈ 0,

энергия, выделившаяся при β-распаде:

Q_β- = M^ат(A,Z)c² − M^ат(A,Z + l)c²;
Q_β+ = M^ат(А, Z)c² − M^ат(A,Z-1)с² − 2m_ec².

    e-захват. (Раньше его называли K-захватом) Помимо испускания е⁺, е^- может произойти процесс захвата электрона с K- или L-оболочки атома, если выполняется условие e-захвата, т.е.

М(А, Z) < М(А, Z + 1) + m_е,

произойдет превращение: (A, Z) → (A, Z-1) + ν. e-захват описывается теми же законами, что и испускание е⁺, е^-. Энергия выделяющаяся при e-захвате

Q_e = M^ат(A,Z)c² − M^ат(A,Z- l)c²;

    Итак, возможны 3 вида β-распадов: испускание е^-, е⁺ и захват е^- с K или L-оболочки атома.

    Спонтанное деление. Деление ядра на осколки (чаще всего на два) сравнимых масс и зарядов.
    Протонная активность. Вылет из ядра протона, т.е. происходит превращение
(A,Z) → р + (A-1,Z-1).
    Двупротонная активность: A,Z) → 2р + (A-2,Z-2).
    При протонной и двупротонной радиоактивности протоны проникают через кулоновский потенциальный барьер благодаря туннельному эффекту. Это явление наблюдается для нейтронодефицитных ядер с Z < 50.
    Все типы распадов обычно сопровождаются испусканием γ-квантов из возбужденных продуктов радиоактивного распада. Иногда вылетают α-частицы, которые в этом случае называются длиннопробежными.

10.2. Вероятности переходов и период полураспада

    Число ядер, распадающихся в единицу времени

− dN/dt = λN(t)

пропорционально числу ядер N(t): имеющихся в наличии в момент t, λ − вероятность распада в единицу времени. Интегрируя по t, получим число ядер, нераспавшихся к моменту времени t:

N(t) = N₀e^-λt,

N₀ − число ядер в момент t = 0.
    Время Т, необходимое для того, чтобы число радиоактивных ядер уменьшилось от N до N/2: называют периодом полураспада, т.е.

N₀e^-λ(t+T)/N₀e^-λt = e^-λT ≡ 1/2,

отсюда

λT = ln2 = 0.693.

Замечено, что распад происходит тем быстрее, чем больше энергия перехода E_d.

Пример:
Распад ядра ²³²Th → ²²⁸Ra + α имеет период полураспада Т = 1.41·10¹⁰ лет, а Е_d = 4.08 МэВ.
Распад ядра ²²⁴Th → ²²⁰Ra + α имеет период полураспада Т = 1.05 с, а Е_d = 7.31 МэВ.
    Период полураспада ²³²Th отличается от периода полураспада ²²⁴Th в 5·10¹⁷ раз, при этом энергия распада изменяется всего в 1.8 раза, α-частицы, испускаемые короткоживущими ядрами, имеют большую энергию, чем α-частицы из долгоживущих ядер.

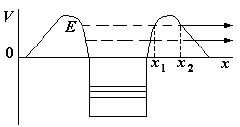Рис. 83: Иллюстрация туннельного эффекта.

    Отмеченные особенности связаны с условием прохождения α-частицы через кулоновский потенциальный барьер ядра − так называемый туннельный эффект. Туннельный эффект есть квантово-механическое явление. Описывая α-частицу волновой функцией, подчиняющейся уравнению Шредингера, можно вычислить прозрачность кулоновского потенциального барьера и вероятность испускания α-частицы ядром. Прозрачность кулоновского потенциального барьера  −

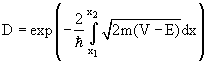
    Туннельный эффект могут испытывать α-частицы, находящиеся на энергетических уровнях с энергией Е > 0 (рис. 83).

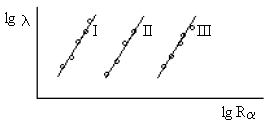Рис. 84: Теорема Гейгера-Неттола (эмпирический закон). I − урановое семейство (U), II − ториевое семейство (Th), III − актино-урановое семейство (U).

    Классификацию радиоактивных ядер можно выполнить, используя зависимость вероятности радиоактивного распада от энергии испущенных α-частиц. Эта зависимость сформулирована в теореме Гейгера-Неттола (рис. 84)

lg λ = A − lg R_α + B,

где R_α − пробег α-частицы, связанный с ее энергией.
    В природе существует три радиоактивных семейства: урановое, ториевое и актино-урановое. Конечными продуктами радиоактивных превращений в этих семействах являются изотопы свинца

I −	238U	→ 206Pb,	A = 4n + 2
II −	232Th	→ 208Pb,	A = 4n
III −	235U	→ 207Pb,	A = An + 3

n − целое число.
    Члены радиоактивных семейств находятся в равновесии между собой.

10.3 Среднее время жизни и ширина уровня

    Статистическая интерпретация закона распада позволяет установить временной интервал τ, определяющий промежуток времени от момента образования нуклида до его распада:

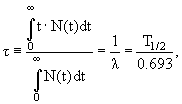
поэтому τ называют средним временем жизни нестабильного уровня. Оно связано с естественной шириной уровня Г соотношением

Г·τ = ћ;   τ = ћ/Г (или τ = 1/Г).

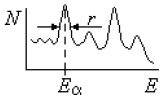Рис. 85: Иллюстрация ширины Г − энергетического уровня.

   Поэтому часто время жизни объекта (ядра или частицы) определяют через ширину уровня Г, которая поддается измерению. Это есть ширина линии в линейчатом спектре или ширина резонанса (рис. 85).
    Указаные соотношения − следствие соотношения Гайзенберга ΔЕ·Δt ≥ ћ. Нестабильному уровню, существующему в течение времени порядка τ, соответствует волновой пакет шириной ΔЕ ≥ ћ/τ.
    Процесс радиоактивного распада − случайный процесс и описывается законом Пуассона: его вероятность

    Радиоактивные распады могут происходить за счет слабых, электромагнитных и сильных процессов. Различия между этими процессами проявляются в величине времени жизни или ширины уровня Г.
    Времена жизни адронов, распад которых происходит за счет сильных процессов, определяются ядерным временем (~ 10^-23÷10^-24 с).
    Если распад адрона происходит за счет электромагнитного взаимодействия, то время жизни составляет величину ~ 10^-16 с. Распады адронов за счет слабых сил протекают за времена
~ 10^-8÷10^-10 с.
    Распады радиоактивных ядер происходят, как правило, за счет слабых процессов. Времена жизни радиоактивных ядер колеблются в очень широких пределах, в то время как энергии распада (или энергии α-частиц) − в очень узких.
    γ-Распад − это не ядерное превращение, а изменение энергетического состояния ядра. γ-излучение сопровождает α- и β-распады. Радиоактивный распад может быть не только самопроизвольным, но и искусственным.

10.4 Искусственная радиоактивность

    Искусственная радиоактивность подчиняется тем же законам, что и естественная, с той разницей, что распадающиеся частица или ядро должны находиться в возбужденном состоянии. Возбуждение может произойти либо вследствие какой-нибудь реакции, в которой образовались распадающаяся частица или ядро, либо из-за искусственного перевода их в возбужденное состояние.
    Искусственные радиоактивные изотопы разных ядер широко используются в медицине и в прикладных отраслях промышленности.
    Радиоактивный распад − частный случай ядерной реакции, но происходит только при Q > 0.

Литература

1. Широков Ю.М., Юдин Н.П. Ядерная физика. -М.: Наука, 1972.
2. Ландау Л.Д. Лекции по физике (под ред. Смородинского).