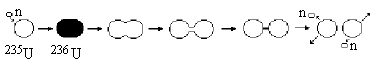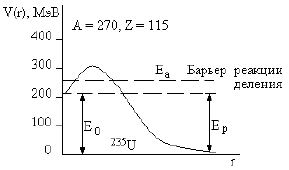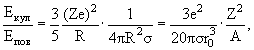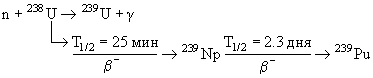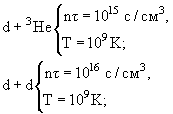Будем рассматривать реакции, происходящие при столкновении двух частиц:
1 + 2 = 1 + 2 + 3 + ... + i + ...

    1.  Закон сохранения 4-импульса (p_x,p_y,p_z,iE):
сохранение энергии Е₁ + Е₂ = Е'₁ + Е'₂ + ... + Е'_n + Q
Q > 0 − экзотермическая реакция, Q < 0 − эндотермическая реакция;
сохранение импульса ₁ + ₂ = '₁ + '₂ + • • • + '_n.
    2.  Закон сохранения электрического заряда

Q₁ + Q₂ = ∑Q_i.

    3.  Закон сохранения числа барионов (барионного заряда В − для частиц и числа нуклонов А − для ядер).
    4.  Закон сохранения лептонного заряда (L_e, Lμ, L_τ).
    5.  Закон сохранения полного момента количества движения.
    6.  Закон сохранения четности в сильных взаимодействиях.
    7.  Закон сохранения изотопического спина.
    8.  Закон сохранения квантовых чисел (странность, чарм и прелесть).
    9.  Закон сохранения зарядового сопряжения (С-инвариантность).

    Набор законов сохранения определяется типом взаимодействия. В слабых взаимодействиях некоторые из перечисленных выше законов нарушаются (отсутствуют, например, сохранение четности, С-инвариантности, странности, изотопспина, см. табл. 15).
    Операция зарядового сопряжения переводит частицу в античастицу:

    С-инвариантность в сильных взаимодействиях сохраняется (по крайней мере с 1% точностью), а в слабых − нарушается.
    В сильных взаимодействиях вводится понятие G-четности: G = С· R. Эта операция представляет собой поворот изотопспина на 180° в пространстве изоспина (R-операция, I₃ → −I₃) с последующим зарядовым сопряжением (С-операция)

G|π) = −|π>.

G-четность сохраняется в сильных взаимодействиях.

    Механизмы взаимодействий частиц с ядрами при низких энергиях отличаются от механизмов взаимодействия при высоких энергиях.
    При низких энергиях хорошо работает механизм образования составного ядра Бора, опирающийся на модель жидкой капли.
    При попадании частицы в ядро образуется составное ядро, если энергия частицы E₀ совпадает с энергетическим уровнем составного ядра Е, и происходит резонансная реакция. Это − большой класс реакций.

а + А → С → b + В.

    Резонансная реакция описывается в квантовой механике формулой Брейта-Вигнера:

Чем меньше Г, тем острее резонанс. Сечение образования составного ядра

 Тогда

Г_b/Г − вероятность распада составного ядра по каналу "b", т.е. σ_ab = σ_aC·(Г_b/Г); σ_ab − сечение образования частицы "b" от частицы "а", σ_aC − сечение образования составного ядра С, Г = ∑Г_i −  суммарная вероятность всех каналов реакции, Г_i − парциальные ширины каналов (например, Г_а, Г_b,...).
    Если другая реакция идет с образованием того же составного ядра С, то вероятность реакции

b' + В' →С → b + В

будет σ_b'b = σ_b'C·(Г_b/Г)  и σ_ab : σ_ab' = σ_b'b : σ_b'b'.
    При высоких энергиях этот механизм не работает, т.к. составное ядро не успевает образоваться, но теория Брейта-Вигнера используется для описания рождения частиц через резонансные состояния R при высоких энергиях (см. рис. 86).

Рис. 86: Фейнмановская диаграмма, иллюстрирующая образование частиц через резонансное состояние R.

    В приведенных выше формулах  роль составного ядра С играет резонансное состояние R.
    Прямые ядерные реакции с выбиванием из ядер р, n, d, ³Не, α ... показывают, что эти частицы могут находиться в ядрах в сформировавшемся состоянии.

Нерезонансные ядерные реакции описываются на основе модельных представлении о ядре. Так, при высоких энергиях используется оптическая модель ядра. При изучении взаимодействий частиц высоких энергий с ядрами широкое распространение получили статистические и гидродинамические модели взаимодействия частиц. В оптической модели ядро − сплошная среда для падающих на ядро частиц, преломляющая и поглощающая де-Бройлевские волны. Гамильтониан взаимодействия

H = V{r) + iW{r).

V{r) − потенциал, описывающий рассеяние падающей на ядро частицы; iW(r) описывает процесс поглощения волны в ядре. Этот процесс подбирают обычно из согласования расчета с экспериментом.
    Оптическая модель хорошо описывает упругое рассеяние и дифракционное рождение частиц на ядре. Дифракционное рождение частиц происходит при обмене виртуальной частицей − помероном IР, который имеет нулевые квантовые числа. При таком обмене квантовые числа системы частиц до и после реакции совпадают (рис. 87а).
    Для описания обменных процессов взаимодействия налетающей частицы с ядрами при очень высоких энергиях можно использовать также квантово-хромодинамическую модель (КХД-модель) (рис. 876).

Рис. 87: Фейнмановские диаграммы для описания обменных процессов: а − для дифракционного рождения частиц, происходящего при обмене помероном IP, а также для процесса обмена реджеоном R; б − для рождения струи (jet) в результате глу-боконеупругого взаимодействия фотона с партонами нуклона в ядре.

    Доля упругого рассеяния и дифракционного рождения частиц составляет ~ 40% полного сечения. Оба процесса имеют четко выраженную волновую природу.

    Ядерные реакции под действием нейтронов занимают особое место в ядерной физике. Из-за того, что нейтрон не имеет электрического заряда, он свободно проникает в любые атомные ядра и вызывает ядерные реакции. Рассмотрим сначала свойства нейтрона.
    Нейтрон был открыт после предсказания Резерфорда, сделанного в 1920 году.
    В опытах Бете и Беккера (1930 год) ядра бериллия облучались α-частицами и было зарегистрировано нейтральное излучение, природа которого не была определена.

α + Be → нейтральное излучение (какое?, γ?).

В опытах Жолио-Кюри (1932 год) α-частицы направлялись на бериллиевую мишень, а затем на парафиновую, чтобы определить природу нейтрального излучения. После парафиновой мишени наблюдался выход протонов. Схема опыта показана ниже.

α + Be →  парафин → p

    Регистрировались протоны отдачи с Е_р = 4.3 МэВ. Возник вопрос: под действием каких частиц они образовывались?
    Если бы они вызывались γ-квантами, то энергия γ-квантов Е_γ должна была быть ~ 50 МэВ. γ-кванты с такой энергией не могли появиться из указанной реакции.
    Чедвик проанализировал эти эксперименты и предположил, что в результате реакции вылетают нейтральные частицы с массой, сравнимой с массой протона. Далее он поставил опыт в камере Вильсона и наблюдал ядра отдачи азота. Он сравнил эти результаты с результатами опытов Жолио-Кюри, в которых регистрировались протоны отдачи из парафина, и определил массу этой нейтральной частицы из законов сохранения энергии

и импульса

m₁v = m₁v₁ + m_pv_p;

где N − ядро азота; v₁ − скорость нейтральной частицы после столкновения; m₁ − масса нейтральной частицы. Она оказалась близкой к массе протона

m₁ ≈ m_p.

Таким образом, стало ясно, что в опытах Жолио-Кюри протекала реакция, в которой испускались нейтральные частицы − нейтроны:

α + ⁹Ве → ¹²С+ n.

Они, попадая на парафин, выбивали протоны отдачи с энергией Е_р = 4.3 МэВ.

    Свойства нейтрона, полученные из многочисленных экспериментов, представлены ниже:
    масса − m_nc² = 939.5 МэВ, m_n = 1.008665 а. е. м.,
    магнитный момент − μ_n = −1.91μ_я,
    спин − J = ћ/2,
    время жизни − τ_n = (10.61 ±0.16) мин,
    среднеквадратичный радиус − <r_n²> = (0.78 ± 0.18)·10^-2 фм².

    Ядерные реакции не только дают новые сведения о природе и свойствах ядерных сил, но и практически используются в народном хозяйстве и в военном деле. Это в первую очередь относится к ядерным реакциям под действием нейтронов при низких энергиях.

11.4 Источники нейтронов

    Источники нейтронов − это различные ядерные реакции.

Рис. 88: Спектр нейтронов.

    1. Используется смесь радия с бериллием (иногда полония с бериллием), где протекает реакция

α + ⁹Ве → ¹²С+ n + 5.5 МэВ.

    Кинетическая энергия нейтрона Т распределена по спектру
(рис. 88).
    При распаде Ra образуются α-частицы с энергией 4.8 МэВ и 7.7 МэВ. Они вступают в реакцию с ⁹Ве и генерируют поток нейтронов. Разброс по энергии нейтронов связан с тем, что α-частицы разных энергий создают нейтроны разных энергий. Ядро углерода ¹²C образуется в основном и возбужденном состояниях.
    Выход нейтронов ~ 10⁷ нейтронов на 1 г Ra в секунду. Одновременно испускаются γ-лучи.

    2. Другие источники нейтронов − фотоядерные реакции (γ,n), в которых получаются медленные и монохроматические нейтроны.

γ + ²H → p + n, Q = -2.23 МэВ.

    Используется ThC" (²⁰⁸Tl). Он испускает γ-кванты с Е_γ ~ 2.62 МэВ и Е_n ~ Е_р; Т_n ~20 кэВ.

    3.  Фоторасщепление Be фотонами с энергией Е_γ = 1.78 МэВ

γ + ⁹Ве → ⁸Ве + n, Q = -1.65 МэВ; Т_n ~ 100 кэВ.

    4. Вылет нейтронов под действием ускоренных дейтонов с E_d = 16 МэВ в реакции

²H + ⁹Be → ¹⁰B + n + 4.3 МэВ.

    Е_n = 4 МэВ, выход 10⁶ нейтронов в секунду.

    5.  Реакция ²H + ²H → ³Не + n + 3.2 МэВ,
    D + D (лед из тяжелой воды), i?n = 2.5 МэВ.

    6.  Облучение дейтонами трития

²H + ³H → ⁴Не + n + 17.6 МэВ.

    Поскольку эта реакция экзотермическая, дейтоны ускоряются до энергии E_d = 0.3 МэВ в газоразрядных трубках. Образуются монохроматические нейтроны с Е_n ~ 14 МэВ.
    Этот источник нейтронов используется в геологии.

    7.  В реакциях срыва под действием дейтонов с E_d ~ 200 МэВ на тяжелых ядрах образуются n с
Е_n ~ 100 МэВ.

11.5 Ядерные реакторы, цепная ядерная реакция

    Самый мощный источник нейтронов − ядерные реакторы − устройства, в которых поддерживается управляемая цепная реакция деления.
    В  реакторе происходит деление ядер U и образуются нейтроны с Е_n от 0 до 13 МэВ, интенсивность источника 10¹⁹ нейтронов/с см2. Процесс деления идет под действием нейтронов, беспрепятственно проникающих в ядра из-за отсутствия кулоновского потенциального барьера.
    При делении ядра образуются радиоактивные осколки и испускается 2-3 n, которые снова вступают в реакцию с ядрами U; идет цепной процесс (рис. 89).

n + ²³⁵U → ²³⁶U → ¹³⁹La + ⁹⁵Мо + 2n

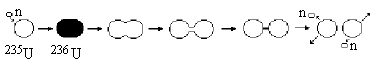
Рис. 89: Иллюстрация деления ядра 235U.

    Для описания процесса деления ²³⁵U используется модель жидкой капли, в которой работает формула Вайцзеккера. После попадания нейтрона в ядро урана происходит конкуренция между поверхностной энергией нового ядра и энергией кулоновского расталкивания. В итоге под действием кулоновских сил ядро делится на два более легких ядра.
    Энергия Q, освобождающаяся при делении ядра (A,Z)

(A,Z) → 2(A/2,Z/2) + Q,

вычисляется с использованием формулы Вайцзеккера

Q = 2ε(A/2,Z/2) − ε(A,Z) = (1 − 2^1/3)·а_сим·A^2/3 + (1 − 2^2/3)·а_кул·Z²·A^-1/3;

Q (МэВ) = -4.5A^2/3 + 0.26·Z²A^-1/3, ε −  удельная энергия связи: Е_св/А. Для ядра ²³⁵U Q = 180 МэВ.

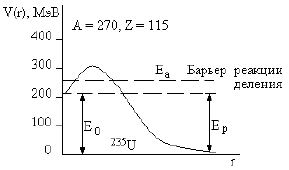
Рис. 90: Потенциальная энергия ядра в зависимости от расстояния до центра ядра (сплошная кривая), E0 − основное состояние, E0 + Еа − возбужденное состояние, Еа − энергия активации.

    Для того, чтобы ядро разделилось, в него должна быть внесена энергия Е > Е_а, где Е_аРис. 90: Потенциальная энергия ядра в зависимости от расстояния до центра ядра (сплошная кривая), E₀ − основное состояние, E₀ + Е_а − возбужденное состояние, Е_а − энергия активации
(рис. 90).
    Мерой способности ядер к делению служит отношение энергии кулоновского отталкивания протонов к энергии поверхностного натяжения:

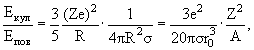
где Z²/A − параметр деления, чем он больше, тем легче ядро делится; Z²/A = 49 критическое значение параметра деления.
    Иллюстрация процесса деления ядра приведена на рис. 91.
    В ядерном реакторе процесс деления ядер многократно повторяется в результате образования многих поколений деления. В 1-м акте деления ²³⁵U возникает в среднем 2.4 нейтрона. Время жизни одного поколения ~ 10 с. Если происходит рождение K поколений, то образуется ~ 2^K нейтронов через время ~ 2·10^-6 с. Если K = 80, число нейтронов будет 2⁸⁰ ~ 10²⁴ − это приведет к делению 10²⁴ атомов (140 г урана). Выделяющаяся при этом энергия 3·10¹³ вт равна энергии, образующейся при сжигании 1000 тонн нефти.

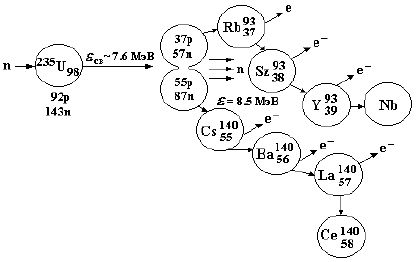
Рис. 91: Процесс деления ядра, протекающий в ядерном реакторе.

    В реакциях деления энергия выделяется в виде тепла. Отвод тепла из реактора осуществляется теплоносителем, к которому предъявляются особые требования. Он должен обладать большой теплоемкостью, слабо поглощать нейтроны и иметь низкую химическую активность. Не будем обсуждать конструктивные особенности элементов ядерного реактора. Заметим только, что при попадании тепловых нейтронов на ядро ²³⁵U образуются быстрые нейтроны, а реакция идет только на медленных нейтронах. Следовательно, необходимо замедлить быстрые нейтроны. Это происходит в замедлителе. В качестве замедлителя используется углерод или тяжелая вода. Остановка процесса деления реализуется с помощью ядер кадмия, которые захватывают образующиеся нейтроны. Таким образом, в конструкцию ядерного реактора обязательно входит замедлитель нейтронов (углерод) и кадмиевые стержни, поглощающие образующиеся нейтроны.
    В реакторах используется природный уран ₂₃₈U (99.3%) и обогащенный ₂₃₅U (0.7%). ²³⁵U делится под действием тепловых нейтронов. ₂₃₈U используется в реакторах на быстрых нейтронах.
    Процессы, происходящие в реакторе, характеризуются следующими вероятностями:
    ν − количество образованных быстрых нейтронов;
    ε − коэффициент размножения быстрых нейтронов;
    Р − вероятность нейтрону дойти до тепловой энергии;
    ƒ − вероятность захвата нейтрона в процессе замедления;
    σ_t/σ_tot − вероятность вызвать реакцию деления.

Произведение этих вероятностей дает оценку коэффициента размножения k тепловых нейтронов в ядерном реакторе:

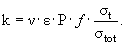
    Цепная реакция идет, если k > 1; входящие в коэффициент размножения величины имеют следующие значения: ν = 2.47; ε = 1.02; Р = 0.89; ƒ = 0.88; σ_t/σ_tot = 0.54.
    Таким образом, k_∞ = 1.07 для реактора бесконечных размеров. В реальных условиях к_эф < k_∞, т.к. часть нейтронов уходит из реактора.
    В реакторах на быстрых нейтронах (²³⁹Ри и ²³⁸U) происходит следующий процесс:

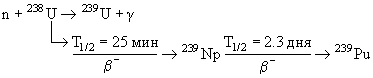
    В результате этой реакции воспроизводится ²³⁹Рu. Образовавшийся плутоний вступает в реакцию с нейтроном: n + ²³⁹Рu, образуется ν = 2.41 нейтронов.
    Число ядер ²³⁹Ри удваивается через каждые 7-10 лет.
    Реакция деления атомных ядер используется для получения атомной энергии. Ядерные реакторы работают на многих атомных электростанциях.

11.6 Реакции слияния, синтез легких ядер

    Другим источником атомной энергии может служить синтез легких атомных ядер. Легкие ядра связаны менее прочно, и при их слиянии в тяжелое ядро выделяется больше энергии. Кроме того, термоядерные реакции чище из-за отсутствия сопровождающих их радиоактивных излучений, чем цепные реакции деления.
    Для получения термоядерной энергии могут быть использованы следующие реакции синтеза:

d + d = ³He + n + 4 МэВ,
d + d = t + р + 3.25 МэВ,
d + t = ⁴Не + n + 17.б МэВ,
³Не + d = ⁴Нe + р + 18.3 МэВ,
⁶Li + 2di = 2 ⁴Не + 22.4 МэВ. J

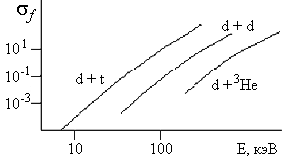Рис. 92: Зависимость эффективного сечения слияния ядер от их кинетической энергии. σƒ − сечение реакции.

    Энергия ядер, вступающих в реакцию, должна быть достаточной для преодоления кулоновского потенциального барьера. На рис. 92 показана энергетическая зависимость сечений некоторых реакций. Как видно из рисунка, синтез ядер дейтерия d и трития t является наиболее предпочтительным. В этой реакции синтеза низок кулоновский потенциальный барьер и велико сечение взаимодействия при малых энергиях сливающихся ядер. Для протекания реакции необходимо иметь достаточную концентрацию этих ядер в единице объема и достаточную температуру разогретой плазмы.
    Число актов слияния R_ab в единицу времени в единице объема определяется соотношением

R_ab = n_a·n_b·w_ab(T).
w_ab(T) = σ_ab·v_ab,

где n_a, n_b − число ядер a, b; σ_ab − эффективное сечение реакции, v_ab − относительная скорость частиц в плазме, Т − температура. В результате реакции освобождается энергия

W = R_ab·Q_ab·τ,

где R_ab − число актов слияния, Q_ab − энергия, выделившаяся в 1 акте, τ − время.
    Пусть n_a = n_b = 10¹⁵ ядер/см³, Т = 100 кэВ. Тогда W ~ 10³ вт/см³ с.
    В самоподдерживающейся термоядерной реакции должно выделяться больше энергии, чем идет на нагрев и удержание плазмы. Затраты на нагрев n_a = n_b = 2n частиц до температуры Т: 3n·kТ: k − постоянная Больцмана. Таким образом, надо удовлетворить условию:

n²·w_ab·Q_ab·τ > 3nkТ

(высвобождающаяся энергия > энергии нагрева).
    Лоусон сформулировал следующее условие для реакции слияния d + t:

nτ > 10¹⁴ с·см^-3,

где nτ − параметр удержания. На рис. 93 показана зависимость этого параметра от температуры. Реакция идет, если nτ > ƒ(T). Температура Т ~ 2·10⁸ K соответствует энергии 10 кэВ. Минимальное значение параметра удержания nτ = 10¹⁴ с/см³ для реакции d + t достигается при температуре 2·10⁸ K.

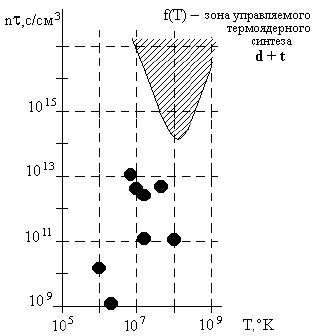
Рис. 93: Зависимость параметров удержания от температуры. Заштрихованная область ƒ(Т) − зона управляемого термоядерного синтеза для реакции d + t. • − значения параметров, достигнутые на различных установках к 1980 году.

    Для других реакций:

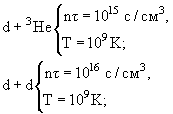
    Удержание плазмы, имеющей необходимые условия для протекания реакции, реализуется в установках типа Токамак с помощью магнитного поля. Такие установки работают в России и в ряде других стран. Как видно из рис. 93, режим управляемого термоядерного синтеза пока не достигнут.
    Делаются попытки получить необходимые для термоядерного синтеза условия с помощью лазерных установок. В этом случае небольшой объем, в котором заключены ядра дейтерия и трития, обжимается со всех сторон лазерным излучением. При этом ядра дейтерия и трития нагреваются до нужной температуры. Лазерный термояд требует введения коэффициента 100, т.к. велика бесполезная энергия, идущая на накачку лазера.
    Попытки осуществить управляемый термоядерный синтез в лабораторных условиях наталкиваются на ряд трудностей.

1. 1.  До сих пор не удается получить устойчивый режим высокотемпературной плазмы.
2. 2.  Велики энергетические потери в плазме даже из-за малых концентраций примесей атомов с большими Z.
3. 3.  Не решена "проблема первой стенки" в Токамаке, ограничивающей плазму реактора (поток нейтронов ее разрушает).
4. 4.  В природе отсутствует радиоактивный тритий t с периодом полураспада Т_1/2 = 12.5 лет, поэтому существует проблема воспроизводства трития в реакции

n + ⁷Li = α + t + n.

    До сих пор не удалось преодолеть эти трудности и получить управляемую термоядерную реакцию синтеза.
    В естественных условиях реакции термоядерного синтеза протекают на Солнце и в звездах.

Литература

1. 1.  Широков Ю.М., Юдин Н.П. Ядерная физика. -М.: Наука, 1972.
2. 2.  Капитонов И.М. Введение в физику ядра и частиц. -М.: УППС, 2002.