Ядерные модели

Основанием для ее введения служит сходство ядерной материи с жидкостью. К таким свойствам следует отнести: несжимаемость ядра, постоянство ядерной плотности: р ~ const, свойство насыщения ядерных сил.

В модели предполагается, что средний свободный пробег до взаимодействия Асв <С 2R ядра. Ядро − сильно связанная система частиц. Энергия связи (см. п. 8.2) определяется выражением

Е_св = αА − βA^2/3 − γZ²A^-l/3 − ξ(N−Z)²/A + δA^-3/4.

    Модель описывает: энергию связи ядра, ядерные реакции при низких энергиях, идущие через составное ядро Бора, реакции деления ядер.
    Модель не описывает некоторые члены в формуле для энергии связи ядра, например энергию спаривания, существование и особую устойчивость магических ядер.
    В ряде случаев ядро можно представить не как жидкость, а как газ, состоящий из нуклонов. Тогда можно использовать модель Ферми-газа.

9.2. Модель Ферми-газа

Основанием для ее введения служит то обстоятельство, что незначительная часть объема ядра занята нуклонами: поскольку размер нуклона в ядре ~ 0.45 фм (а свободного нуклона ~ 0.8 фм), то нуклонами занята только 1/50 объема ядра.
Нуклоны в ядре − вырожденный Ферми-газ, заключенный в потенциальной яме (рис. 75).

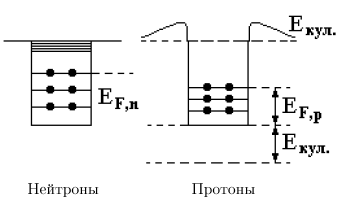
Рис. 75: Схематическое изображение потенциальных ям для ядер, содержащих нейтроны и протоны.

Вводятся следующие предположения.

Температура ядра очень мала, и нуклоны занимают низкие энергетические уровни − вырожденный Ферми-газ (из фермионов, т.к. J = 1/2).
Нуклоны заполняют все уровни до энергии Ферми: Е_F = p_F²/2m ~ 50 МэВ, p_F − импульс Ферми, нуклоны в ядре испытывают Ферми-движение.

В соответствии с принципом Паули на каждом энергетическом уровне может находиться не более двух нуклонов.

Модель описывает следующие характеристики ядра.

Число состояний нуклонов в шестимерном фазовом объеме

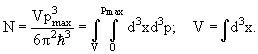
Полное число протонов (или нейтронов) равно 2N (т.к. каждый уровень занят двумя частицами):

Энергию Ферми, поскольку

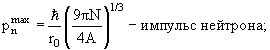
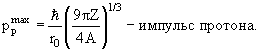
Используя эти величины, получим для энергии Ферми Е_F = p_F²/2m ~ 50 МэВ

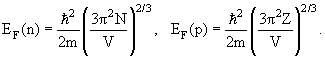
Среднюю энергию, приходящуюся на 1 нуклон,

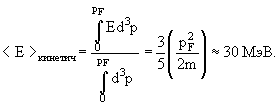
Все уровни с Е < Е_F заняты.

Эта модель так же, как модель жидкой капли, не описывает существование особо устойчивых магических ядер. Для их описания служит оболочечная модель ядра.

9.3. Оболочечная модель ядра

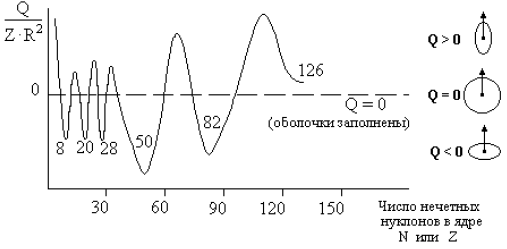
    Модели жидкой капли и Ферми-газа − грубые модели. Хотя они и описывают важнейшие свойства ядер, но не объясняют свойства возбужденных состояний ядер и особую стабильность магических ядер, когда Z или N (или оба числа) равны одному из магических чисел: 2, 8, 20, 28, 50, 82, 126 (в атоме магические числа равны: 2, 10, 18, 36, 54, 86).
    Основанием для введения модели служит наличие магических чисел у ядер, свидетельствующее, что у ядер так же, как у атомов, существуют оболочки.
    Таким образом, главным предположением в модели является наличие оболочки ядра − совокупности близких по энергии уровней.
Можно также предположить, что в ядре действует самосогласованный эффективный потенциал, который имеет приблизительно такой же вид, как и распределение плотности ядерного вещества в форме распределения Вудс-Саксона (рис. 76).
    Потенциал Вудс-Саксона: 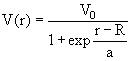для нейтронных оболочек.
Для протонных оболочек добавляется V_кул(r).

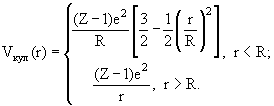
Параметры V_0p и V_0n выбирают из опыта, например для ядра ²⁰⁸Pb₈₂ V_0n = 45.7 МэВ, V_0p = 57.9 МэВ.

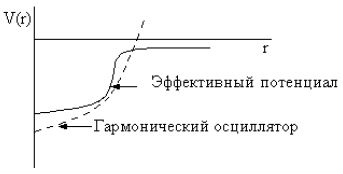
Рис. 76. Самосогласованный эффективный потенциал (сплошная линия). Пунктиром представлен вид потенциала для гармонического осциллятора.

R = 7.6 фм, b = −0.17 фм², а = 0.65 фм.

Для других ядер используются другие эмпирические значения:

где V₀ = 53 МэВ, R = 1.28A^1/3 фм, b = 0.263(1 + 2(N-Z)/2) фм² (b − постоянная спин-орбитального взаимодействия).

V = Н_вз = V(r) + U(r) · ,

Спин-орбитальное взаимодействие подтверждается оболочечной моделью.
Как и в атоме, для описания ядерных оболочек вводятся следующие обозначения: n − главное квантовое число, определяющее расположение уровней при одном и том же номере оболочки l. Оно принимает значения: 1, 2, 3, .. . l −имеет значения 0, 1, 2, 3, ...

s, p, d, ƒ, ... оболочки.

При данном l есть два подуровня j = l ± 1/2.
Оболочечный уровень нуклона в ядре обозначается: 1d_5/2, т.е. n = 1, l = 2, полный момент j = l + s = 5/2; (2j + 1) нуклонов на каждом уровне.

Модель описывает как идет заполнение ядерных оболочек. В табл. 16 приводятся значения магнитных моментов μ, вычисленных и измеренных экспериментально для каждого ядра.

Таблица 16. Оболочечная модель ядра

Сравнение μ_эксп и μ_теор свидетельствует о справедливости предложенной модели. Для ядер, у которых заполнены оболочки, спин равен нулю. Таким образом, спин и магнитный момент ядра определяются непарным нуклоном, находящимся в данном состоянии.
Модель не объясняет деформированные ядра. Для объяснения существования деформированных ядер используются значения квадрупольных электрических моментов и обобщенная модель ядра.

Рис. 77. Иллюстрация вращения дополнительного нуклона вокруг остова.

Модель рассматривает заполненную оболочку как остов, и в ее поле вращается дополнительный нуклон (рис. 77). Остов ядра деформируется валентным нуклоном, что приводит к появлению квадрупольного электрического момента ядра Q (см. п. 8.5). Модель используется для описания деформированных атомных ядер, которые могут быть вытянутыми или сплюснутыми относительно оси симметрии ядра. Ось симметрии ядра, как правило, совпадает с направлением суммарного спина ядра. О деформации ядра можно судить по величине квадрупольного электрического момента ядра.
На рис. 78 показано поведение квадрупольного электрического момента для разных ядер. Значение Q = 0 соответствует сферически симметричным атомным ядрам, значения Q > 0 − вытянутым атомным ядрам, Q < 0 − сплюснутым атомным ядрам.

Рис. 78: Иллюстрация поведения квадрупольного электрического момента для разных ядер.

Экспериментальные данные о квадрупольных электрических моментах ядер см. на рис. 74.
Модель согласуется с поведением квадрупольного электрического момента для разных ядер, который по определению равен:

Q = Z ∫r² ρ(r) (3 cos² θ − l)d³r.

Переходим к рассмотрению ядерных моделей, использующихся при описании процессов, происходящих при высоких энергиях.

9.5. Оптическая модель ядра

    Ядро представляет собой "серую" полупрозрачную сферу с определенными коэффициентами преломления и поглощения.
    При попадании на такую сферу упавшая частица (волна) испытывает все виды взаимодействия, характерные для распространения света в полупрозрачной оптической среде: отражение, преломление, поглощение.
    Усредненный потенциал в таком ядре имеет вид U(r) = V + iW, т.е. содержит мнимую часть, учитывающую поглощение падающей волны. В разных вариантах оптической модели потенциал
U(r) представляют в виде прямоугольной ямы.
    Модель позволяет вычислять упругое рассеяние, суммарное сечение всех неупругих процессов, а также угловые характеристики рассеянных ядром частиц.
    Действительную часть оптического потенциала обычно выбирают в виде потенциала Вудса-Саксона. Мнимая часть потенциала выбирается пропорциональной объемному или поверхностному поглощению. Модель требует подбора параметров для каждого ядра и для каждой энергии упавшего адрона.
    Вид оптического потенциала для рассеяния адронов на ядрах зависит от параметров удара и может определяться либо кулоновским взаимодействием при больших параметрах удара, либо процессами сильного взаимодействия при меньших параметрах удара. При параметрах удара меньших радиуса ядра доминирует поглощение. При этом картина рассеяния выглядит как интерференция кулоновского рассеяния и дифракционного рассеяния адрона на черной сфере.

9.6. Модель Глаубера

    Рассеяние быстрой частицы на ядре сводится к последовательному рассеянию ее на отдельных частицах мишени. Результирующее рассеяние получается усреднением по положениям рассеивающих центров. Рассеяние на отдельной частице носит характер дифракционного. После первого соударения налетающая частица выбывает из пучка и частицы мишени, расположенные за рассеивающим центром, не участвуют в рассеянии. Этот процесс описывается так называемой глауберовской поправкой, которая учитывает экранировку последующих нуклонов.
    В глауберовской модели налетающая частица последовательно взаимодействует с нуклонами ядра-мишени. (Аналогия − рассеивание биллиардного шара на неподвижных шарах.) Этот подход вполне оправдан при не очень высоких энергиях. В релятивистском случае частица-снаряд взаимодействует одновременно не с одним, а сразу с несколькими нуклонами мишени, что приводит к возникновению дополнительной экранировки. Учет образования неупругих промежуточных состояний был выполнен Грибовым и носит название грибовской поправки.
    В основе модели Глаубера лежат три гипотезы, основанные на волновых свойствах частиц и ядер.

Фазовые сдвиги, возникающие при прохождении через ядро падающей частицы-волны, вызываемые отдельными нуклонами ядра, суммируются.
Рассмотрение прохождения частицы через ядро проводится в представлении параметра удара (геометрическая оптика).
Ядерная волновая функция не успевает измениться за время прохождения частицы через ядро.

Это − дифракционная модель, т.к. она рассматривает дифракцию падающей волны на отдельных нуклонах ядра.
Как известно, сечение взаимодействия частицы с ядром для процессов сильного взаимодействия может быть представлено в виде

σ_tot= σ_упр + σ_неупр + σ_{квазиупр}.

В модели Глаубера сечение имеет вид

где А − число нуклонов в ядре, σ_рр − сечение нуклон-нуклонного взаимодействия в ядре, G(A) − поправки на упругое и неупругое экранирование. Таким образом, первый член описывает рассеяние на А нуклонах, а сумма последующих − поправки на экранирование. G_упр − глауберовская поправка, G_неупр − грибовская поправка.
Как видно из рис. 79, если включается упругое или неупругое экранирование, направление движения частицы не меняется. Эти эффекты нельзя обнаружить на опыте, но необходимо учитывать при вычислении полных сечений взаимодействия частиц с ядрами.

Рис. 79: Иллюстрация поведения падающей частицы внутри ядра при включении упругого и неупругого экранирования.

9.7. Гидродинамические модели

Ядро − гидродинамическая система, которую можно описать, введя уравнение состояния, плотность энергии, температуру, энтропию и другие гидродинамические характеристики ядерной материи.
Гидродинамические модели служат для описания сильновзаимодействующей ядерной материи, которая отождествляется с идеальной жидкостью. Вводятся локальные переменные, зависящие от координат х: плотность энергии ε(х), давление р(х), плотность энтропии s(x), температура Т(х), 4-скорость u_μ(х). Для описания идеальной жидкости используется тензор энергии-импульса

Т^μν = (ε + p)u^μu^ν − g^μνp

и закон сохранения

∂_μТ^μν = 0.

Уравнение состояния релятивистской идеальной жидкости

ε = 3р, р = π²Т⁴n/90,

где n − число степеней свободы. (При низких температурах идеальный газ π-мезонов n = 3; при высоких температурах идеальный газ (кварков и глюонов)

Связь между введенными переменными при отсутствии химического потенциала μ = 0 имеет вид ε + р = Ts, s = dp/dT. Тогда закон сохранения тензора энергии-импульса может быть записан в виде:

(u^μu^ν – g^μν)∂_μ(lnТ) + u^μ∂_μu^ν = 0,
∂_μ(su^μ) = 0, u_μ·u^μ = 1.

Эти соотношения образуют замкнутую систему, из которой можно в принципе определить Т и u_μ при наступлении термодинамического равновесия и выбранных начальных условиях.
    Указанный путь реализуется во многих гидродинамических моделях. Эти модели используются при описании процессов взаимодействия частиц с ядрами или ядер с ядрами при высоких энергиях и дают предсказания о множественном рождении частиц в зависимости от энергии сталкивающихся частиц, о поведении импульсных распределений вновь рожденных частиц .
    Рассмотренные выше модели, в которых ядро обладает свойствами жидкости и описывается формулой Вайцзеккера (модель жидкой капли), либо наоборот ядро рассматривается как идеальный Ферми-газ, что позволяет определить энергию движения нуклонов в ядре, а также обо-лочечная модель ядра, дающая понимание существования магических ядер, и обобщенная модель ядра, учитывающая форму атомных ядер, используются при невысоких энергиях. При более высоких энергиях используются оптическая модель ядра, модель Глаубера-Ситенко, статистические и гидродинамические модели.
    Таким образом, простое перечисление моделей показывает, насколько сложной системой является атомное ядро.

Литература

Валантэн Л. Субатомная физика: ядра и частицы. -М.: Мир, 1986.
Физика элементарных частиц и атомного ядра, т. 34, №1, 2003, с. 147-188.
Никитин Ю.П., Розенталь И.Л. Ядерная физика высоких энергий. -М.: Атомиздат, 1980.

9. Ядерные модели

9.1. Модель жидкой капли

9.2. Модель Ферми-газа

9.3. Оболочечная модель ядра

9.4. Обобщенная модель ядра

9.5. Оптическая модель ядра

9.6. Модель Глаубера

9.7. Гидродинамические модели