Статические характеристики атомных ядер и элементарных
частиц определяют свойства частиц в невозбужденном состоянии, в отличие от
динамических, проявляющихся при ядерных превращениях и различных реакциях.
Важнейшими статическими характеристиками ядра являются:
атомный номер, определяющий число протонов в ядре Z,
число нейтронов в ядре N,
массовое число − количество нуклонов в ядре А,
энергия связи Есв,
спин J,
изотопический спин I,
пространственная четность Р,
размеры частиц R,
дипольный магнитный момент μ,
электрический квадрупольный момент Q
статистика, которой подчиняются частицы, и другие квантовые числа.
Главнейшей характеристикой всякой частицы является ее
масса (масса покоя). Частицы − это квантовые системы, имеющие возбужденные
состояния (см. п. 1.3.2).
Для атома основное состояние определяется массой нейтрального
атома, состоящей из массы ядра и массы атомарных электронов.
Международная единица массы (а.е.м.) равняется 1/12 массы
атома
12С.
1 а.е.м. = 1.66043·10-24 г = 931.481 МэВ = 1 D (дальтон).
Возбужденные состояния ядер характеризуются энергиями
возбуждения в МэВ. Для ядер они малы по сравнению с их массой (см. рис. 3).
Для элементарных частиц положения энергетических уровней
характеризуются энергиями, соответствующими массам покоя частиц (МэВ, ГэВ, см.
рис. 2). Самая легкая частица − электрон:
mе ~ 10-27
г, а Е = mес2 = 0.511 МэВ. Более тяжелая − мюон: mμс2
= 105 МэВ ~ 206 mес2. Еще тяжелее протон: mр
~ 2000 mе. Атомные ядра имеют массу до 260 mр, т.е.
массы частиц различаются в миллионы раз. Поэтому способы определения масс частиц
очень разнообразны (см. п. 6).
Массы составных частиц − адронов и ядер − это мера энергии,
содержащейся в частице. Она определяется суммой масс конституентов за вычетом
энергии связи этих составляющих и может быть определена из модельных
представлений о ее составе.
Адроны состоят из кварков: барионы − из трех кварков; мезоны
− из двух (кварка и антикварка). Так утверждает кварковая модель, и это
утверждение подтверждается на опыте.
Можно составить соотношения для адронов, используя их
кварковый состав: р, n, Λ, Σ+, Σ-, Ξ0, Ξ-
и т.д. Предположим, что энергия связи между кварками εqq
одинакова в любом адроне. Тогда для октета барионов будем иметь следующие
соотношения:
| uud | m(p) = 2m(u) + m(d) − 2ε(ud)/c2 − ε(uu)/c2 |
| ddu | m(n) = 2m(d) + m(u) − 2ε(ud)/c2 − ε(dd)/c2 |
| uus | m(Σ+) = 2m(u) + m(s) − 2ε(us)/c2 − ε(uu)/c2 |
| dds | m(Σ-) = 2m(d) + m(s) − 2ε(ds)/c2 − ε(dd)/c2 |
| ssu | m(Ξ0) = 2m(s) + m(u) − 2ε(us)/c2 − ε(ss)/c2 |
| ssd | m(Ξ-) = 2m(s) + m(d) − 2ε(ds)/c2 − ε(ss)/c2 |
Массы кварков невозможно измерить непосредственно, но можно скомбинировать массы известных частиц, предположив, что энергии связи между кварками одинаковы. Тогда для некоторых комбинаций получим
m(р) − m(п) + m(Ξ0) − m(Ξ- ) + m(Σ-)
− m(Σ+) = 0,
m(Ξ*-) − m(![]() -)
= m(Ω-)/3 − m(Δ-).
-)
= m(Ω-)/3 − m(Δ-).
Эти соотношения могут быть проверены, т.к. массы частиц
получены в соответствующих экспериментах.
Аналогичная процедура, исходящая из гиптезы, что ядро состоит
из Z протонов и N нейтронов, приводит к выражению: M(Z, A) = Zmр + Nmn
− Есв(Z, A)/c2; A=Z + N.
Масса ядра меньше суммы масс протонов и нейтронов на величину
энергии связи Есв/c2. Эта величина для ядер очень велика и
поддается прямому измерению.
8.2. Энергия связи
Важнейшей статической характеристикой атомных ядер является энергия связи: Есв − энергия, необходимая для полного расщепления ядра на р и n. Можно определить энергию связи через mр и mn:
Eсв(Z,A) = [Zmр + Nmn − M(Z, A)]c2.
Все величины, входящие в эту формулу, известны. Так, например,
для α-частицы:
Есв = (2·1.007276 + 2·1.0086665 − 4.001523)а.е.м.
= 28.3 МэВ, а соответствующая ей величина массы Есв/c2
~ 4·10 г, что составляет ~ 0.7% от полной массы α-частицы. Если энергии
связи известны, то можно рассчитать процессы превращения ядер. Так, для
отделения протона от ядра (Z, А) нужна энергия
Ep = Eсв(Z,A) − Eсв(Z-1,A-1).
Для удобства вводят удельную энергию связи ε = Есв/A,
приходящуюся на один нуклон.
Энергия связи зависит от атомного
номера ядра. Анализ этой зависимости дает обширную информацию о свойствах ядер.
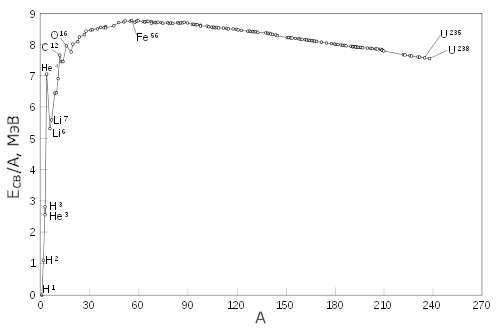
В первом приближении энергия связи постоянна и равна ~ 8 МэВ на нуклон − это
свойство насыщения ядерных сил (рис. 69а).
a)
б)
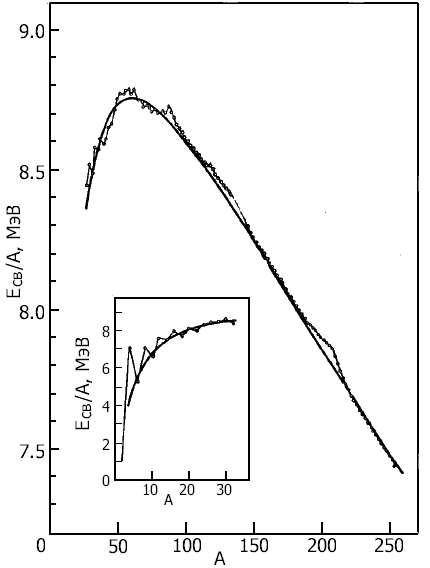
Рис. 69. Удельная энергия связи ε = Есв/A в зависимости от атомного номера ядра.
Более детально поведение энергии связи в зависимости от
атомного номера показано на рис. 696, из которого видно, что максимум ε = 8.8
МэВ у ядра железа (А = 56). Это наиболее стабильное ядро.
Легчайшие ядра сливаются в более тяжелые с выделением энергии
связи − термоядерной энергии (рис. 696, врезка).
Уменьшение ε в область легких ядер − следствие поверхностных
эффектов, когда нуклонами на поверхности ядра используются не все валентности, ε
уменьшается на величину, пропорциональную поверхности ядра ~ A2/3.
ε(Z) при фиксированном А ведет себя так, как показано на рис. 70.
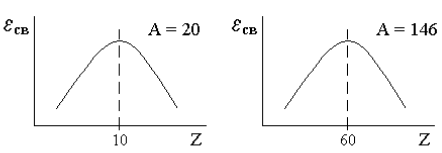
Рис. 70. ε(Z) при фиксированном А.
Как видно из рисунка, при А = 20
максимум приходится на значение Z ~ А/2. Равное число р и n создают лучшие
условия для существования стабильных ядер.
Это − следствие квантово-механического принципа Паули и того,
что энергия взаимодействия (рn) в среднем больше, чем (рр) и (nn). Это − энергия
симметрии. Она отрицательна по знаку и определяется величиной (N-Z)2/А.
Тяжелые ядра делятся на более легкие с выделением энергии
связи − атомной энергии. Уменьшение есв в области тяжелых ядер − следствие
электростатического отталкивания протонов. Кулоновская энергия отталкивания ~ Z2/A1/3.
ε(Z,N) больше для ядер с Z и N четным и меньше для ядер с Z и
N нечетным, что свидетельствует о существовании энергии спаривания нуклонов в
ядре. При спаривании энергия связи возрастает на 2÷3 МэВ. Эта дополнительная
энергия учитывается величиной δ(A,Z).
На основе этих данных Вайцзеккер получил полуэмпирическую
формулу для энергии связи (рис. 71):
Есв = αА − βA2/3 − γZ2A-l/3 − ξ(N−Z)2/A + δA-3/4,
где α = 15.75 МэВ; β = 17.8 МэВ; γ = 0.71 МэВ; ξ = 22 МэВ;
 .
.
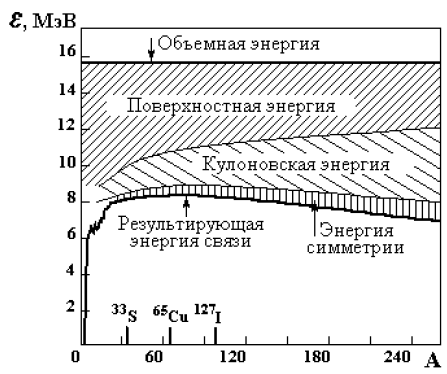
Рис. 71. Иллюстрация поведения отдельных членов в формуле Вайцзеккера.
Особенности формулы Вайцзеккера: 1) резкая разница между α = 15.75 МэВ и ε ~ 8 МэВ, объясняется тем, что коэффициент а вычислен для бесконечно большого ядра с одинаковым числом р и n; 2) при А = 40÷50; 90, 130, 210 εсв отличается от вычисленной по формуле на ~ 1% (рис. 696); эти отклонения приходятся на зоны магических ядер, у которых число протонов и нейтронов равно одному из следующих магических чисел: 2, 8, 20, 28, 50, 82, 126; если и число протонов и число нейтронов равны одному из магических чисел, то такие ядра называются дважды магическими: 4Не2, 16O8, 40Са20, 48Са20, 208Pb82.
8.3. Протон-нейтронная диаграмма
Атомные ядра могут существовать только в ограниченной области значений А и Z (рис. 72). Вне этой области, которая называется областью стабильности, ядро, если и возникает, то мгновенно (за время 10-24 с) распадается.
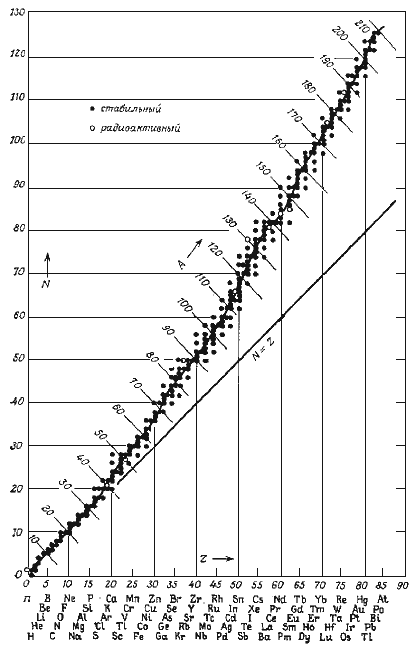
Рис. 72: Зависимость между числом нейтронов N и протонов Z для разных значений А
(протон-нейтронная диаграмма)
Теоретические границы области стабильности определены, но
экспериментально подойти к этим границам достаточно трудно, т.к. времена жизни
ядер около этих границ очень коротки.
Изучение протон-нейтронной диаграммы приводит к следующим
заключениям.
- Известны ядра от Z = 0 до Z = 107. Искусственно получены ядра вплоть до Z = 116.
- Нет стабильных ядер с Z = 0, 43, 61 и Z > 84.
- Известны ядра от А = 1 до А = 263.
- Нет стабильных ядер с A = 5, 8 и А > 210.
- Свойства ядер зависят от четности Z и N. Особо стабильными являются ядра, у которых Z и N четные. Всего 4 ядра с Z и N нечетными: 2H1, 6Li3, 10B5, 14N7.
- При малых А у ядер число р равно числу n, а с ростом А увеличивается доля нейтронов.
- Большинство химических элементов имеет много изотопов. Больше всего их у олова Sn (10 стабильных изотопов). Ядра Be, Na, Al имеют только по одному стабильному изотопу.
8.4. Спин и магнитный момент ядра
Спин − собственный момент количества движения
микросистемы, ее внутреннее квантовое число. В физике частиц эта характеристика
является основополагающей для решения проблемы классификации частиц. Частицы,
имеющие
полуцелый спин, образуют класс фермионов, а частицы с целым спином nћ (n = 0,1,
2,...) − класс бозонов. Различие между фермионами и бозонами колоссальное.
Фермионы подчиняются запретам Паули и
описываются статистикой Ферми. Все фундаментальные частицы (лептоны и кварки)
являются фермионами.
Бозоны подчиняются статистике Бозе, фундаментальные бозоны в
физике частиц определяют тип взаимодействия. Они являются переносчиками
взаимодействий (см. п. 2).
Спин ядра определяется количеством нуклонов: при четном числе
нуклонов ядро имеет целый спин, при нечетном − полуцелый, т.к. нуклоны являются
фермионами с полуцелым спином.
Таким образом, ядра могут быть как фермионами, так и
бозонами. Поскольку нуклоны в ядре движутся и имеют орбитальный момент L, то
полный момент ядра является суммой орбитального и спинового моментов нуклонов
![]() =
=
![]() +
+
![]() .
.
Природа спина у адронов до сих пор не вскрыта. Ее пытались
понять, исходя из внутренней структуры адронов, состоящих из партонов. Однако
такой подход пока не привел к решению проблемы спина адронов.
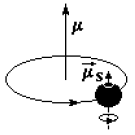 Рис. 73. Орбитальный и спиновый магнитные моменты частицы с зарядом ze и массой m. |
Согласно классической электродинамике при вращении частицы
с зарядом ze и массой m и обладающей механическим моментом ћ![]() ,
возникает магнитный момент, пропорциональный механическому моменту
,
возникает магнитный момент, пропорциональный механическому моменту
![]() .
Таким образом, аналогом классического момента
.
Таким образом, аналогом классического момента
![]() является магнитный момент
орбитального движения
является магнитный момент
орбитального движения
![]() ,
,
где eћ/2mc − магнетон. При наличии спина S у частицы и отсутствии
орбитального движения магнитный момент
![]() или μs = gs·μB, где gs −
гиромагнитное отношение (рис. 73). У электрона Дирака μ = μB = eћ/2mec
− магнетон Бора.
или μs = gs·μB, где gs −
гиромагнитное отношение (рис. 73). У электрона Дирака μ = μB = eћ/2mec
− магнетон Бора.
Магнитный момент протона измеряется в ядерных магнетонах
μя = eћ/2mpc −, магнитный момент протона μp =
2.8μя. Магнитный момент нейтро-на μn
= −1.9μя.
Магнитный момент частицы может быть измерен по взаимодействию
ее магнитного момента с внешним магнитным полем. Измерение магнитного момента
дает возможность определить спин частицы.
8.5. Квадрупольный электрический момент ядра
Квадрупольный электрический момент ядра характеризует
отклонение распределения электрического заряда в ядре от сферически
симметричного и может служить для изучения формы атомного ядра.
Квадрупольный электрический момент ядра является тензором и
определяется соотношением
Q = Z ∫r2 ρ(r) (3 cos2 θ − l)d3r,
где θ − полярный угол радиуса вектора относительно оси симметрии ядра, r −
расстояние элемента заряда от начала координат.
Для сферически симметричного ядра Q = О, вытянутое вдоль оси
симметрии ядро имеет Q > О, а сплюснутое − Q < 0.
На рис. 74 представлены экспериментальные данные о значениях
квад-рупольных электрических моментов для разных ядер.
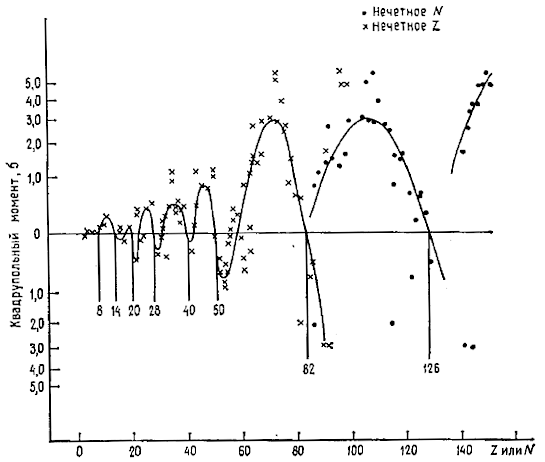
Рис. 74. Экспериментальные данные о зависимости квадруиольиых электрических
моментов от Z или N. Цифры на рисунке − магические числа.
8.6. Изотопический спин
Изотопический спин I характеризует число адронов, входящих
в так называемый изотопический мультиплет. Это число равно 2I + 1. Изотопический
спин адронов, как и обычный спин, может принимать значения целых и полуцелых
чисел (0, 1/2, 1, 3/2 и т.д.). Простейшим изотопическим мультиилетом является
изотопический дублет, состоящий из двух частиц: протона Iz
= +1/2 и нейтрона Iz = −1/2. Iz − проекция изотопического
спина на ось Z. Изотопический триплет состоит из трех частиц: π+, π0,
π-. Адроны, входящие в мультиплет, имеют близкие массы и близкие
свойства по отношению к сильному взаимодействию. Существуют и другие
изотопические мультиплеты, например Ξ0, Ξ-; K+,
K0;
К0, К-; D+, D0; Σ+, Σ0,
Σ- и др.
Полный изотопический спин системы адронов вычисляется по
правилам, аналогичным правилам сложения обычных спинов, и в случае ядра может
принимать значения от 1/2(N−Z) до l/2(N+Z): где N − число нейтронов, Z − число
протонов в ядре. Суммарный изотопический спин ядра определяет число различных
зарядовых состояний с примерно одинаковой энергией связи. Изотопический спин
сохраняется в процессах сильного взаимодействия и нарушается в слабых и
электромагнитных взаимодействиях.
Изотопический спин связан с изотопической инвариантностью
сильного взаимодействия. Изотопическая инвариантность ядерных сил состоит в том,
что в ядерных взаимодействиях протон и нейтрон можно рассматривать как два
состояния одной частицы (нуклона), отличающиеся проекцией Iz изотопического
спина.
8.7. Законы сохранения
Кинематической характеристикой частицы является 4-импульс
![]() (px,py,pz,iE),
где px, py, pz − компоненты трехмерного вектора
импульса, а Е − энергия частицы.
(px,py,pz,iE),
где px, py, pz − компоненты трехмерного вектора
импульса, а Е − энергия частицы.
В процессах сильного взаимодействия сохраняются следующие
величины:
2) электрический заряд Q;
3) барионный заряд B;
4) лептонный заряд L (имеются три лептонных заряда Le, Lμ, Lτ);
5) спин J − собственный момент количества движения;
6) изотопический спин I;
7) странность s;
8) четность пространственная Р;
9) четность временная Т;
10) четность зарядовая С;
11) четность комбинированная СР и СРТ;
12) квантовые числа s (strange), с (charm), b (beauty), t (truth);
13) G-четность G.
В
электромагнитных взаимодействиях не сохраняются G-четность и
изотопический спин I, а в слабых взаимодействиях не сохраняются Р-четность,
С-четность, Т-четность, G-четность и изотопический спин I.
Для наглядности все законы сохранения сведены в табл. 15.
Знак + обозначает, что данная величина сохраняется.
Таблица 15. Законы сохранения
| Взаимодействия | Q | B | L | С | Р | T | CРТ | G | I |
| Сильные | + | + | + | + | + | + | + | + | + |
| Слабые | + | + | + | − | − | − | + | − | − |
| Электромагнитные | + | + | + | + | + | + | + | − | − |
Квантовые числа s, с, b, t сохраняются в сильных взаимодействиях и не сохраняются в слабых.
Литература
- Широков Ю.М., Юдин Н.П. Ядерная физика. -М.: Наука, 1972.
- Капитонов И.М. Введение в физику ядра и частиц. -М.: УППС, 2002.
- Аминева Т.П., Сарычева Л.И. Фундаментальные взаимодействия и космические лучи. -М.: Эдиториал УРСС, 1999.