Ионизационные потери тяжелых заряженных частиц с зарядом z в среде с зарядом Z описываются формулой Бете-Блоха
.
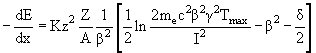где
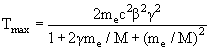− максимальная кинетическая энергия, которая может быть
передана частицей с массой М свободному электрону в одном соударении;
для А
= 1 г·моль-1 (А − атомная масса поглотителя) и NA = 6.022·1023 моль-1 −
число Авогадро; I − средний потенциал ионизации; δ − поправки, учитывающие
эффект плотности среды.
На рис. 37 изображена зависимость потерь энергии от импульса для разных частиц: мюонов, пионов и протонов. Ионизационные потери заряженных
частиц происходят при передаче энергии электронам атомов вещества. Формула
получена в предположении, что энергия передается одиночному электрону от тяжелой заряженной частицы, проходящей на расстоянии
b от частицы, при этом учитываются все разумные значения b от bmах до
bmin,
при которых передается электрону энергия от Еmin до Еmах. Поэтому формула
Бете-Блоха дает средние потери энергии тяжелой заряженной частицы. В формулу
входят определенные выше следующие величины: NA − число Авогадро, радиус
электрона и его масса rе и mе, заряд частицы z, заряд вещества и его атомный вес
Z и А, скорость частицы β, Лоренц-фактор частицы γ, ионизационный потенциал I, максимально передаваемая в одном соударении энергия Тmах, эффект плотности,
учитывающий экранировку поля заряженной частицы в результате поляризации атомов
вдоль ее пути, δ.
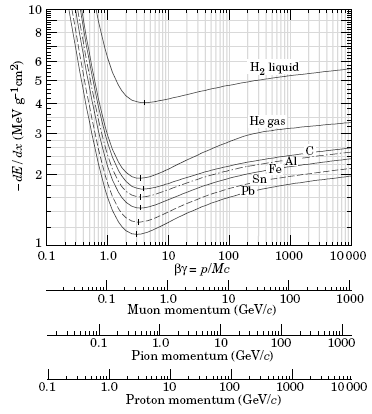
Рис. 37. Ионизационные потери тяжелых заряженных частиц в разных веществах в зависимости от импульса частицы βγ.
Формула Бете-Блоха описывает средние потери энергии, а распределение потерь
энергии вокруг среднего значения описывается распределением Ландау (см. далее
рис. 46).
Заряженные частицы при прохождении через вещество помимо ионизационных потерь
теряют энергию на радиационное (тормозное) излучение. На рис. 38 показаны потери
энергии мюонами в медном поглотителе. Представлены все возможные потери энергии от ионизационных до радиационных в
зависимости от энергии мюонов.
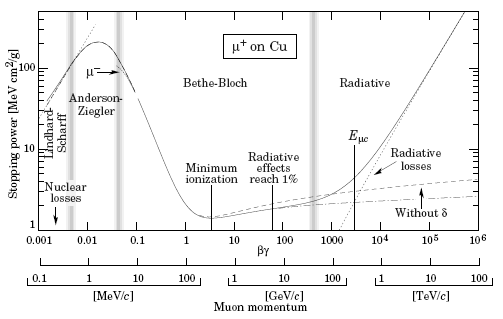
Рис. 38. Потери энергии мюонами − dE/dx = a(E) + b(E)E в медном поглотителе (Сu), а(Е) − ионизационные потери, b{Е) − образование е+е--пар, тормозное излучение, фотоядерные эффекты.
Радиационные потери энергии для тяжелых частиц начинают сказываться только
при очень высоких энергиях.
Для легких частиц − электронов и позитронов − помимо ионизационных потерь
следует учитывать потери энергии на тормозное излучение.
Поскольку поперечное сечение для образования тормозного излучения обратно
пропорционально квадрату массы частицы, то радиационные потери, не существенные
для тяжелых частиц, играют определяющую роль для легких.
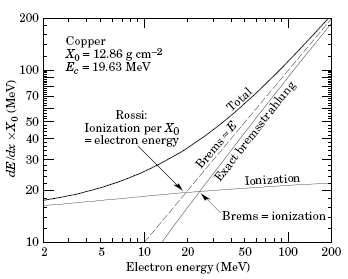
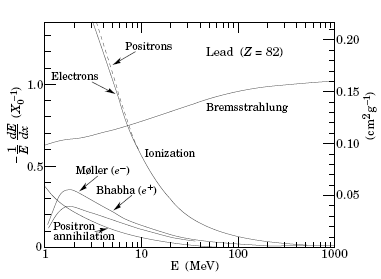
На рис. 39 показаны энергетические потери электронов в меди и свинце в зависимости от энергии электронов.
 a |
 б |
Рис. 39. Энергетические потери электронов в зависимости от энергии электрона: а − в меди, б − в свинце. Х0 − радиационная длина, Ес − критическая энергия Екр.
При рассмотрении процессов, происходящих с легкими частицами, вводится радиационная единица длины Х0: определяющая толщину вещества, при прохождении которого энергия электрона или позитрона вследствие тормозного излучения уменьшается в е раз:
При изучении электромагнитных процессов длина пути частицы в веществе t
измеряется в радиационных единицах длины.
Энергия, при которой ионизационные потери сравниваются с потерями на
тормозное излучение, называется критической энергией Екр.
5.2. Процессы, происходящие с фотонами в веществе
Перечислим основные процессы, происходящие с фотонами при сравнительно невысоких энергиях, в результате которых фотоны теряют свою энергию.
- Фотоэлектрический эффект (пропорционален Z5) приводит к поглощению фотонов при соударении с атомными электронами. Поперечное сечение обычно воспроизводит структуру атома.
- Комптоновское рассеяние (пропорционально Z) происходит на свободном электроне. Этот процесс приводит к образованию комптоновских электронов. При энергиях выше нескольких МэВ 90% энергии передается комптоновскому электрону.
- Образование пар (сечение пропорционально Z2 + Z) происходит так же, как процесс тормозного излучения, но имеет пороговую энергию 2mе = 1.022 МэВ. Как и тормозное излучение, этот процесс преобладает при высоких энергиях. Если процесс образования пар является доминирующим, то средний свободный пробег фотона λph = (9/7)X0.
На рис. 40 представлен ход поперечных сечений взаимодействия фотонов с ядрами
атомов углерода и свинца при умеренных энергиях.
При энергиях до 1 МэВ существенным процессом является фотоэффект. В области
энергий от 1.5 кэВ до 1.5 МэВ происходит комптоновское рассеяние фотонов на
электронах. При энергиях более 1 МэВ начинает преобладать процесс образования
е+е--пар фотонами.
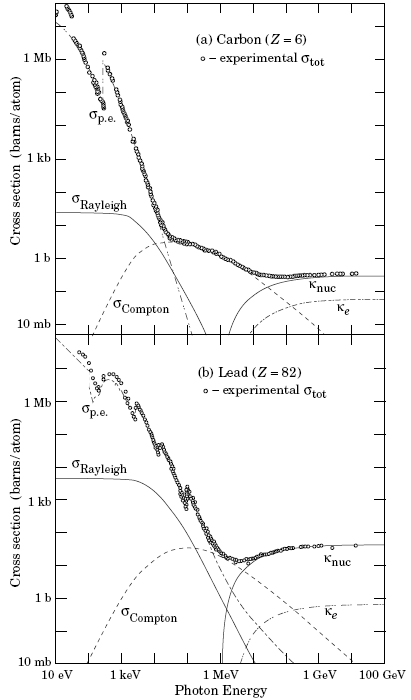
Рис. 40. Поперечные сечения взаимодействий для фотонов: а − в углероде и b −
в свинце.
5.3. Электромагнитные каскады
Если происходят процессы тормозного излучения фотонов легкими частицами и
образования электрон-позитронных пар фотонами при энергиях выше нескольких
десятков МэВ, то возникают электромагнитные каскады. Число частиц в таких
каскадах на глубине t: выраженной в радиационных единицах длины, растет как N(t)
= 2t, а энергия, уносимая каждой частицей, уменьшается как E(t) = E0/2t. Этот
процесс происходит до тех пор, пока энергия не станет равной критической Екр.
После этого доминирующим процессом станут ионизационные потери энергии,
комптоновское рассеяние и поглощение фотонов. Таким образом, максимальное число
частиц в каскаде образуется при tmах = ln(Ео/Екр)/ln2. Полное число частиц в
электромагнитном каскаде будет ~ 2Е0/Екр, а полная длина каскада − E0X0/
Екр. Такие каскады развиваются в электромагнитных калориметрах, использующихся в
физике высоких энергий для определения энергии частицы. Энергия частицы
(электрона, фотона), образующей электромагнитный каскад, определяется как
площадь под каскадной кривой:
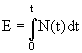. Энергетическое разрешение
калориметра зависит от энергии
σ(Е)/Е ~ 1/√Е. На рис. 41 показана каскадная кривая.
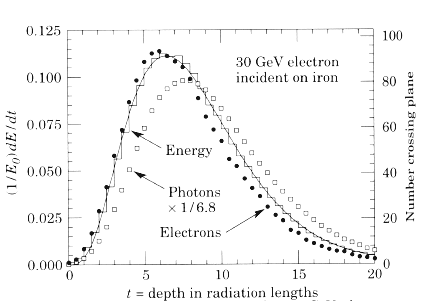
Рис. 41. Каскадная кривая в железе для электрона (•) и фотона (о) с энергией
30 ГэВ.
Литература
- THE EUROPEAN PHYSICAL JOURNAL C. Particles and Fields. Zietschrift fur Physik С v.15, No.1-4, 2000. Springer.
- Journal of Physics G, Nuclear and Particles Physics, v.33, July 2006 (Review of Particle Physics).
