Результаты измерения поперечных сечений разных типов взаимодействий

Напомним, что процесс взаимодействия характеризуется сечением, которое является релятивистски инвариантной величиной и имеет размерность площади [см²], σ_i = F_i/F, где F_i − число реакций типа i, происходящих за время t; F − число "первичных" частиц, проходящих за то же время через поперечное сечение площадью 1 см²; σ_tot = ∑σ_i − полное сечение. Если в качестве мишени используется водород (протон), то σ_tot = σ_el + σ_inel, если атомное ядро, то σ_tot = σ_el + σ_inel + σ_qinel (σ_qinel − квазиупругое рассеяние).
Изменение поперечных сечений для многих реакций было проанализировано и определена параметризация в виде:

σ(р) = А + Врⁿ + Cln²{p) + Dln(p);

σ в мб, р в ГэВ/с.
Наилучшие значения коэффициентов А, В, С, D и экспоненты n для некоторых реакций показаны в таблице 13.

Таблица 13. Значения коэффициентов при параметризации сечений для разных реакций и импульсов

Реакция	Диапазон импульсов р, ГэВ/с	А	В	n	С	D
γp, tot	3.0÷183	0.147±	−	−	0.0022	-0.017
π⁺р, tot	4.0÷340	16.4±	19.3±	-0.42±	0.19±	−
π⁺р, el	2.0÷200	−	11.4±	-0.4±	0.079±	−
π^-р, tot	2.5÷370	33.0±	14.0±	-1.36±	0.456±	-4.03
π^-р, el	2.0÷360	1.76±	11.2±	-0.64±	0.043±	−
К⁺р, tot	2.0÷300	18.1±	−	−	0.26±	-1.0
К⁺р, el	2.0÷175	5.0±	8.1±	-1.8±	0.16±	-1.3
К^-р, tot	3.0÷310	32.1±	−	−	0.66±	-5.6
К^-р, el	3.0÷175	7.3±	−	−	0.29±	-2.4
рр, tot	3.0÷2100	48.0±	−	−	0.522±	-4.51
рр, el	3.0÷2100	11.9±	26.9±	-1.21±	0.169±	-1.85
р, tot	5.0÷ 1.73·10⁶	38.4±	77.6±	-0.64±	0.26±	-1.2
р, el	5.0÷ 1.73·10⁶	10.2±	52.7±	-1.16±	0.125±	-1.28

На рис. 27 представлены результаты измерения сечений на ускорителях и в космических лучах.

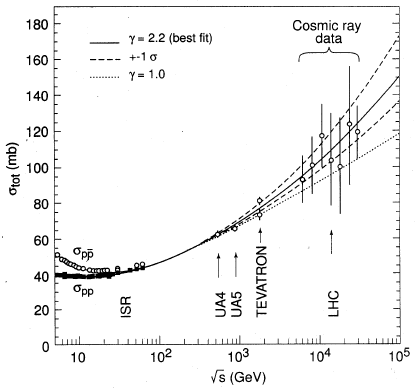
Рис. 27: Зависимость сечений от энергии поперечного сечения для сильных взаимодействий . Данные, полученные в космических лучах (кружки с большими ошибками), не позволяют определить зависимость сечения от энергии. Эта задача будет выполнена на ускорителе LHC.

Реджевская модель по сравнению с аппроксимацией, представленной выше, дает другую зависимость:

(IP − обмен помероном, R_i − обмен ρ, ω, ƒ, a).
E_лаб = s/2m_p [ГэВ2], s = (E₁* + E₂*)².

Зависимости сечений от энергии в системе центра масс (с.ц.м.) по результатам многих измерений, выполненных на ускорителях, представлены на рисунках 28-30.
Поперечные сечения в зависимости от энергии в рр- и рр-соударениях представлены на рис. 28. Плавные коивые соответствуют аппроксимации

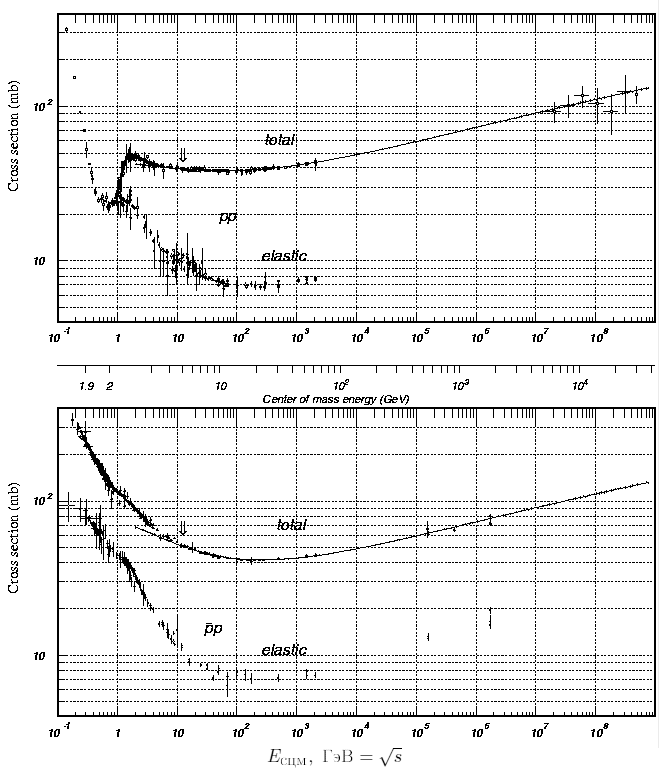
Рис. 28. Зависимость поперечных сечений от энергии для рр- и р-взаимодействий.

Xs^ε + Ys^η, причем для рр- и р-взаимодействий числовые коэффициенты имеют следующие значения: X = 21.7, Y = 98.39. Значения показателей степени для этих реакций: ε = 0.0808, η = 04525; s − квадрат полной энергии в системе центра масс.
Поперечные сечения для π^±p-взаимодействий показаны на рис. 29.

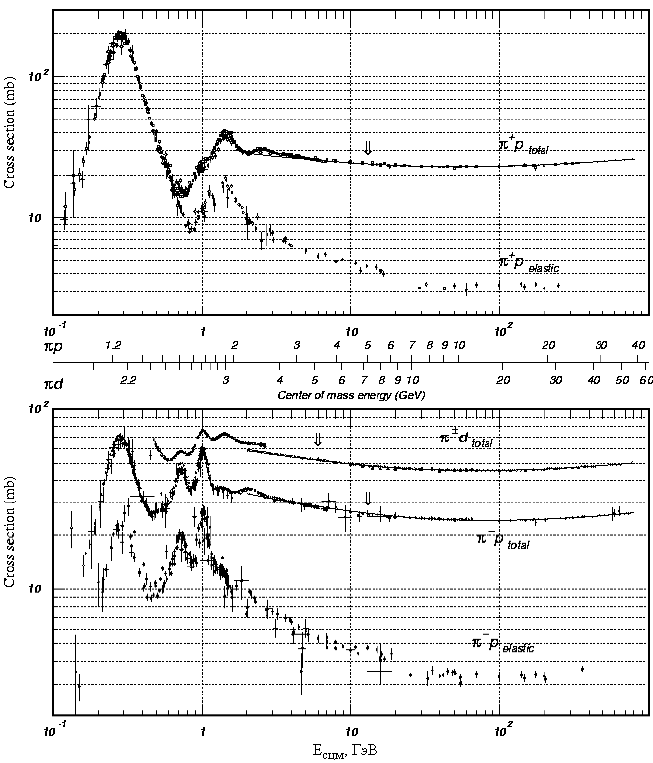
Рис. 29. Зависимость поперечных сечений от энергии для π⁺р- и π^-р-взаимодействий.

Линии, показанные на рисунках, соответствуют аппроксимации Xs^ε + Ys^η, причем числовые коэффициенты имеют следующие значения: для π⁺р-взаимодействий X = 13.63, Y = 27.56; для π^-р-взаимодействий X = 13.63, Y = 36.02. Значения показателей степени ε и η одинаковы для этих реакций: ε = 0.0808, η = 04525; s − квадрат полной энергии в системе центра масс.

Поперечные сечения для К^±р-взаимодействий показаны на рис. 30

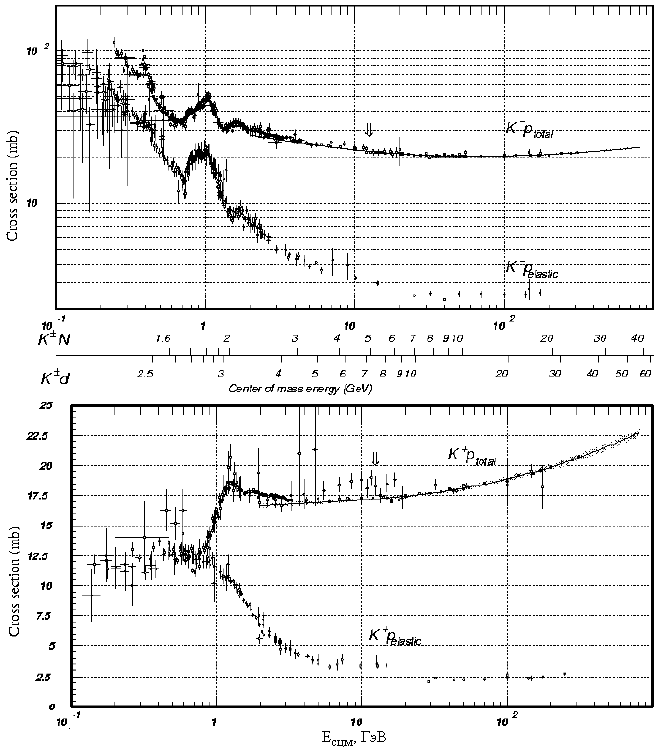
Рис. 30: Зависимость поперечных сечений от энергии для К⁺р- и К^-р-взаимодействий.

Аппроксимации Xs^ε + Ys^η показаны на рисунках сплошными линиями. Числовые коэффициенты имеют следующие значения: для К⁺р-взаимодействий X = 11.82, Y = 26.36; для К^-р-взаимодействий X = 11.82, Y = 8.15. Значения показателей степени г и г] одинаковы для этих реакций: ε = 0.0808, η = 04525; s − квадрат полной энергии в системе центра масс.

4.2. Интерпретация зависимости σ_tot(E)

Исследование зависимости σ_tot(E) есть тест для проверки различных теоретических моделей.

1. Для сильных взаимодействий существует строгое ограничение на рост поперечных сечений с энергией, сформулированное в виде теоремы Фруассара:

σ_tot < A ln²(s/s₀),

A и s₀ − постоянные величины, s − квадрат полной энергии в системе центра масс. Теорема есть следствие принципов аналитичности, унитарности и кроссинг-симметрии.

Полное сечение не может расти быстрее, чем ln²(s/s₀).

2. Упругое сечение 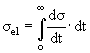изменяется с энергией так же, как σ_tot·(σ_el/σ_tot) ~ const при изменении энергии. Величина <Г> = 2σ_el/σ_tot характеризует среднюю поглощающую способность (непрозрачность) протона при рассеянии протонов и антипротонов на протонах

<Г> =0.361 ±0.010

и эта величина не изменяется во всей области энергии, где наблюдается рост сечений.

Это означает, что рост сечений не связан с увеличением поглощающей способности нуклона, а связан с изменением его размеров.

3. Разные модели предсказывают следующее.

Убывание <Г> с энергией − модель "критического померона".
<Г> ~ const − модель геометрического скейлинга.
Рост <Г> с энергией − струнная модель Кайдалова-Тер-Мартиросяна, основанная на реджевской модели, по которой аппроксимация сечений может быть представлена в виде

Аппроксимация, основанная на реджевской модели, имеет вид

В формуле содержится 5 свободных параметров.

Из экспериментальных данных при энергии 100 ГэВ можно получить следующие соотношения между сечениями:

σ(πp)/σ(pp) = 5/8; σ(Kp)/σ(pp) = 1/2.

4. Если радиус кварка принять равным комптоновской длине его волны ~ h/m_qc, то вычисленные соотношения практически совпадают с экспериментально измеренными (табл. 14).

Таблица 14. Численные значения отношений разных сечений

Отношения сечений	Вычисленные значения	Экспериментально измеренные значения
σ(πp)/σ(pp)	0.66	0.64 ±0.01
σ(Kp)/σ(πp)	0.84	0.81 ±0.08
σ(Δ⁰p)/σ(pp)	0.89	0.89 ±0.05

5. Поведение сечений при низких энергиях до 100 ГэВ имеет нерегулярный характер. Это связано с рождением резонансов, которое инициирует пики в сечениях при соответствующих энергиях.

4.3. Результаты измерения поперечных сечений в электромагнитных взаимодействиях

В квантовой теории описание взаимодействий осуществляется в терминах обмена специфическими квантами (бозонами), связанными с определенным типом взаимодействия. Переносчиками электромагнитных взаимодействий являются фотоны.
Взаимодействия частиц через электромагнитные поля могут быть наглядно представлены диаграммами Фейнмана (рис. 31).

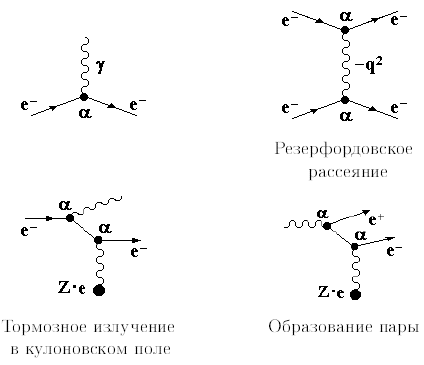
Рис. 31: Диаграммы Фейнмана, иллюстрирующие основные электромагнитные взаимодействия.

    Взаимодействие на расстоянии обычно описывается в терминах потенциала поля, действующего между частицами. В случае электромагнитного взаимодействия между электрическими зарядами Q действует кулоновский потенциал V = Q/r. Электромагнитное взаимодействие лежит в основе всех наблюдаемых электрических, магнитных и электромагнитных явлений. Различные проявления электромагнитного взаимодействия широко используются при конструировании детекторов в физике частиц и ядер, в электротехнике, радиотехнике и электронике. Электромагнитные явления на больших расстояниях описываются уравнениями Максвелла.
    На микроскопическом уровне электромагнитное взаимодействие выражается с помощью токов, структура которых определяется типом взаимодействующих частиц. Электромагнитный ток в квантовой теории поля описывает рождение или аннигиляцию под действием электромагнитного поля пары частица-античастица либо поглощение и рождение заряженной частицы. Электромагнитный ток является нейтральным векторным током заряженных частиц, например для электрона он содержит операторы уничтожения электрона и рождения позитрона. Электромагнитный ток является сохраняющейся величиной.
    Интенсивность электромагнитных процессов в микромире определяется безразмерным параметром α = е² /ћc = 1/137. Процессы, происходящие на микроскопическом уровне описываются квантовой электродинамикой (КЭД), которая является самой точной физической теорией.
    Зависимость поперечного сечения электромагнитного взаимодействия от энергии можно увидеть по результатам измерения взаимодействия фотонов с протонами σ_γp и фотонов с фотонами σ_γγ (рис. 32).

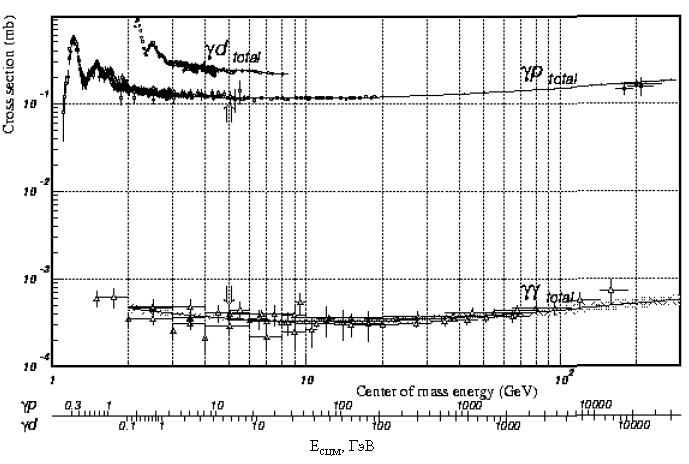
Рис. 32. Зависимость поперечных сечений от энергии для *ур- и 77~столкновений

Для электромагнитных взаимодействий сохраняется аппроксимация в виде Xs^ε + Ys^η, где X = 0.0677, ε = 0.0808; Y = 0.129, η = 0.4525.
Поперечные сечения для других электромагнитных процессов будут рассмотрены дальше.

4.4. Слабые взаимодействия

Изучение слабых взаимодействий продолжалось длительный период.

1896 г. − Беккерель обнаружил, что соли урана испускают проникающее излучение (β-распад тория). Это стало началом исследования слабого взаимодействия.

1930 г. − Паули выдвинул гипотезу о том, что при β-распаде наряду с электронами (е) испускаются легкие нейтральные частицы − нейтрино (ν).

1934 г. − Ферми предложил квантово-полевую теорию β-распада. Распад нейтрона (n) есть следствие взаимодействия двух токов: адронный ток переводит нейтрон в протон (р), лептонный − рождает пару электрон + нейтрино.
Это 4-фермионное контактное взаимодействие с константой Ферми G_F = 1.436·10^-49 эрг·см³.

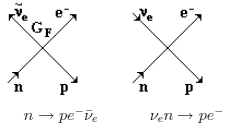
Слабое взаимодействие ответственно за все медленные распады частиц.

1956 г. − Райнес впервые наблюдал реакцию р → nе⁺ в опытах вблизи ядерного реактора.
Ли и Янг объяснили парадокс в распадах K⁺-мезонов (τ ~ θ загадка) − распад на 2 и 3 пиона. Он связан с несохранением пространственной четности. Зеркальная асимметрия обнаружена в β-распаде ядер, распадах мюонов, пионов, K-мезонов и гиперонов.

1957 г. − Гелл-Манн, Фейнман, Маршак, Сударшан предложили универсальную теорию слабого взаимодействия, основанную на кварковой структуре адронов. Эта теория привела к описанию слабого взаимодействия с помощью диаграмм Фейнмана, отличных от 4-фермионного взаимодействия.
В этот период были открыты два принципиально новых явления: нарушение СР-инвариантности и нейтральные токи.
Ландау впервые предположил существование "левых" и "правых" частиц.

1960 - 1961 г. − Глэшоу, Вайнберг, Салам высказали соображение о том, что слабое взаимодействие не является контактным а происходит путем обмена промежуточными векторными бозонами W , Z . W осуществляет взаимодействие через заряженные токи, & Z0 − через нейтральные токи.

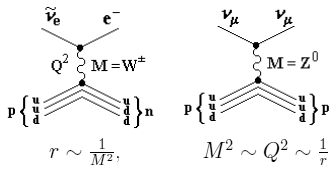
Ледерман в Брукхейвенской национальной лаборатории (БНЛ, США) наблюдал неупругое столкновение нейтрино от распадов π⁺ → μ⁺ν_μ и π^- → μ^-_μ атомными ядрами. В этом эксперименте было установлено различие между нейтрино мюонным ν_μ и нейтрино электронным ν_e, которое послужило поводом для введения лептонных квантовых чисел: L_μ и L_e.

1964 г. − Предсказано существование нейтральных слабых токов и нарушение СР-инвариантности.

1973 г. − Открыты нейтральные слабые токи, предсказанью теорией электрослабого взаимодействия, при взаимодействии нейтрино и антинейтрино с нуклонами.
Обнаружены безмюонные нейтринные реакции, обусловленные взаимодействиями нейтральных токов j⁰.

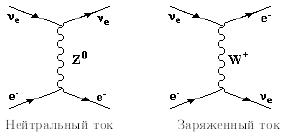
Суммарный нейтральный ток состоит из слагаемых двух типов: левые токи − и правые токи − .

1976 г. − Объяснение слабых ядерных сил перешло на кварковый уровень. После открытия нейтральных слабых токов, переносчиками которых является Z⁰-бозон, было установлено, что полный слабый нейтральный ток содержит вклады всех лептонов и всех кварков:

Заряженный лептонный ток определяется первыми тремя слагаемыми следующей формулы, все остальные члены представляют заряженный кварковый ток:

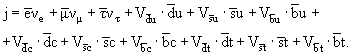
− числовые коэффициенты (у кварковых токов). Полный заряженный ток j описывает большое количество слабых процессов.

1983 г. − На ускорителе SpS (ЦЕРН) в экспериментах под руководством К. Руббиа впервые были зарегистрированы W^±-и Z⁰-6oзоны и определена их масса.

1989 - 1995 г. − На ускорителе LEP (ЦЕРН) определены точные значения масс W^±-и Z⁰-бозонов: m_w = 80.22 ±0.26 ГэВ, m_z = 91.1884±0.0022 ГэВ. Связь между массами W^±-и Z⁰-бозонов существует в виде m_z = m_w/cosθ_w- Из экспериментальных данных по нейтральным токам sin²θ_w = 0.23, где θ_w − угол Вайнберга, который используется при объединении электромагнитных и слабых взаимодействий. В дальнейших экспериментах по изучению слабых взаимодействий значение sin²θ постоянно уточняется.

1991-2001 г. − На ускорителе LEP2 (ЦЕРН) проводилось изучение распадов Z⁰-бозонов, которое показало, что в природе существует только три поколения лептонов: ν_e, ν_μ и ν_τ. Результаты экспериментов ALEPH, DELPHI, L3, OPAL, выполненных на ускорителе LEP2 (ЦЕРН), представлены на рис. 33.

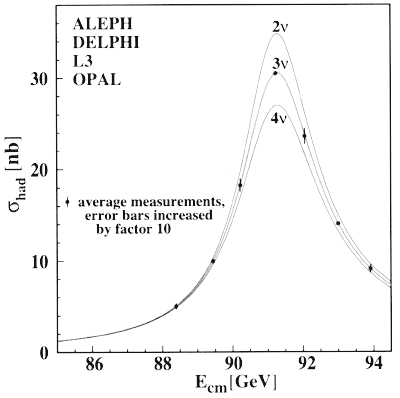
Рис. 33. Поперечные сечения для е⁺е^--аннигиляции в адронные состояния вблизи энергии, равной массе покоя Z⁰. Кривые вычислены в предположении о существовании разных поколений нейтрино (2, 3, 4). Экспериментальные точки, усредненные по разным экспериментам, ложатся на кривую, вычисленную с учетом трех поколений нейтрино.

Исследования, выполненные на этом же ускорителе, были направлены на поиск гипотетических бозонов − Хиггс-бозонов. В результате этих исследований была сделана оценка массы Хиггс-бозона − m_H > 100 ГэВ/с².

1999 г. − В эксперименте DONUT (ФНАЛ, США) впервые было зарегистрировано ν_τ. В детекторе, состоящем из 250 кг ядерных фотоэмульсий, наблюдено 5 событий, вызванных ν_τ с рождением τ-лептона.
В эксперименте NuTeV (ФНАЛ, США) при регистрации 2·10 нейтринных событий и измерении сечения обратного мюонного распада ν_μ + е^- → μ^-ν_e:

σ = (14.2 ± 2.9)·10^-42·E_ν см²

получено новое значение параметра угла смешивания

sin²θ_w = 0.2553 ±0.0019.

2000 г. − При изучении К⁰-распадов получены наиболее точные данные о нарушении СР-инвариантности. Теория предсказывает для отношения долгоживущих K_L-мезонов к корот-коживущим K_S по разным каналам распадов следующее поведение:

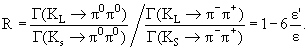
Если параметр (ε'/ε) ≠ 0, то это свидетельствует о прямом нарушении СР-четности. В этом случае по теоретическим оценкам (ε'/ε) = (17 ±6)·10^-4. В эксперименте оказалось, что (ε'/ε) = (19.2 ±4.6)·10^-4.

4.4.1. Осцилляции нейтрино и его масса

    Нерешенным вопросом в физике частиц и ядер остается вопрос о существовании у нейтрино массы, отличной от нуля. Этот вопрос решается во многих экспериментах, среди которых особенно интенсивными являются исследования процесса осцилляции нейтрино ν_е ↔ ν_μ ↔ ν_τ. Длина осцилляции (путь, на котором один аромат нейтрино переходит в другой ν₁ ↔ ν₂) зависит от разности квадратов масс осциллирующих нейтрино . Если существуют нейтринные осцилляции, то это может свидетельствовать, что масса нейтрино m_ν ≠ 0. Заметим, что в Стандартной Модели физики частиц m_ν = 0. Обнаружение у нейтрино массы, отличной от нуля, открывает путь в новую физику.
    Нейтринные осцилляции ν_μ→ ν_еизучались в экспериментах Камиоканде и Супер Камиоканде (Япония). В этих экспериментах получены указания на существование осцилляции атмосферных и солнечных нейтрино. По результатам этих экспериментов была сделана оценка для (Е_ν) ~ 10 ГэВ, Δm_ν² = 3·10^-3 эВ². На ускорителе КЕК (Япония) изучаются осцилляции нейтрино ν_μ→ ν_е на пути L ~ 250 км.
    Эксперименты с нейтрино по изучению осцилляции продолжаются до настоящего времени и будут продолжаться в следующие (по крайней мере) 20 лет. Если будет надежно показано, что осцилляции существуют, надо будет определить массу нейтрино и параметры смешивания. Это позволит решить проблемы дефицита солнечных нейтрино, атмосферных нейтрино, проблему "темной материи".

4.4.2. Поперечное сечение для слабых взаимодействий

В слабых взаимодействиях участвуют разные частицы, но только одна частица − нейтрино − участвует только в слабых взаимодействиях. Поэтому результаты измерения сечений слабых взаимодействий приводим для взаимодействия нейтрино и антинейтрино с нуклонами (рис. 34).

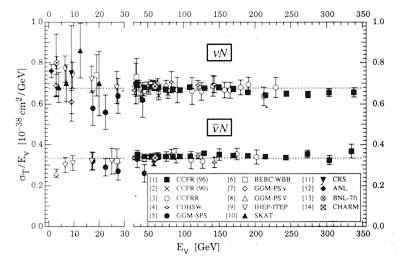
Рис. 34. Сечение взаимодействия нейтрино и антинейтрино с нуклонами в зависимости от энергии по результатам многих экспериментов.

Сечение взаимодействия нейтрино с нуклоном пропорционально энергии нейтрино.

4.4.3. Электрослабые взаимодействия

Идея, лежащая в основе теории электрослабого взаимодействия, состоит в том, что электромагнетизм и слабые силы − проявление единого и более фундаментального закона природы. При очень высоких энергиях события, обусловленные этими силами, неразличимы:

Можно объединить фотон и промежуточные векторные бозоны в семейство из четырех частиц. В таком состоянии все эти бозоны − безмассовые. Затем, вследствие спонтанного нарушения симметрии W^± и Z⁰ приобретают массу, благодаря механизму Хиггса, а фотон остается безмассовым. Механизм Хиггса предусматривает существование хиггсовского поля, носители которого − Хиггс-бозоны.
При объединении электромагнитных и слабых взаимодействий кроме реально существующих W^± и Z⁰ вводятся гипотетические частицы W⁰-и В⁰- бозоны. Они реально не наблюдаются, но входят в линейную комбинацию и образуют поля А и Z⁰.

А = W⁰sinθ_w + B0cosθ_w,
Z⁰ = W⁰cosθ_w− B⁰sinθ_w.

Поля А и Z⁰ реально наблюдаются: А − фотон, Z⁰ − тяжелый векторный бозон, ответственный за нейтральные слабые токи, θ_w − угол смешивания, угол Вайнберга (это свободный параметр теории). Величина угла определяет связь между массами Z⁰- и W-бозонов: m_w = m_z·cosθ_w, a также связь между константой g, характеризующей взаимодействие W^± со слабым током, и константой е, характеризующей взаимодействие фотона с электрическим током: е = g·sinθ_w. Эксперимент дает:
sin²θ_w = 0.2553 ± 0.0019, что приводит к значениям масс

m_w = 80.22 ± 0.26 ГэВ, m_z = 91.1884 ± 0.0022 ГэВ.

Фундаментальные слабые взаимодействия происходят между лептонами и кварками через нейтральные и заряженные токи

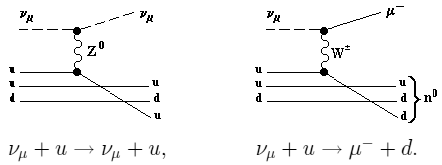
Различие между лептонами и кварками:

1) лептоны образуют токи только со своими нейтрино;

2) если ввести "повернутые" на угол θ_C кварки

d' = d cosθ_C + s sinθ_C,
s' = −d sinθ_C + s cosθ_C,

где θ_C − угол Каббибо, |sinθ_C| ≈ 0.22, θ_C ≈ 13°, то коэффициенты у кварковых токов будут единичные.
Если рассматривать частицы трех поколений: е, μ, τ, ν_e, ν_μ, ν_τ, u, d, s, с, b, t, то полный ток

В теории слабых токов состояния d', s', b', не имеющие определенных масс, являются "истинными частицами".
Это есть "ароматическая" структура слабого взаимодействия.

4.5. Гравитационное взаимодействие

В массовой шкале, изучаемой в физике высоких энергий, гравитационные взаимодействия пренебрежимо малы по сравнению с электромагнитными и другими фундаментальными взаимодействиями.
Гравитационные эффекты проявляются, когда гравитационная энергия системы сравнима с ее полной энергией, т.е.

G_NM²/r ≈ Mc²,

где константа взаимодействия G_N = 6.67·10^-11 м³кг^-1с^-2.
Это может произойти, когда Мс² = 10¹⁹ ГэВ. Эта масса называется планковской, а соответствующая ей комптоновская длина волны

~ 10^-33 см.

Эта величина интерпретируется как фундаментальная длина, а время

~ 10^-43 с

как элементарный временной интервал.
Константа связи для гравитационного взаимодействия

если m = m_p.

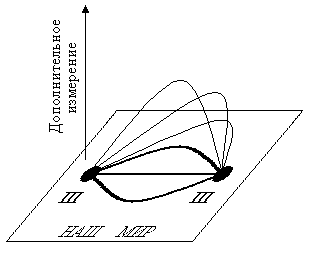Рис. 35: Схематическое изображение трехмерного мира в виде плоскости и дополнительных измерений, выходящих за пределы плоскости. Жирными черными точками изображены объекты, находящиеся в трехмерном мире. Жирные линии между ними − силовые поля, действующие между этими объектами. Тонкие линии, выходящие за пределы плоскости − силовые линии, не измеряемые в трехмерном мире и существующие в дополнительных измерениях.

Возникают вопросы:

Почему гравитация так слаба?
Что приводит к огромному расхождению между фундаментальной шкалой для гравитации и шкалой для других взаимодействий?

    В настоящее время рассматривается такое объяснение.
    Гравитация уникальна среди других сил − она действует в дополнительном измерении. Это означает, что большой гравитационный поток не проявляется в нашем трехмерном мире. Он разбивается по многим дополнительным измерениям, а наш трехмерный мир можно представить в виде плоского мира (рис. 35).
    Модель дополнительных измерений предполагает, что гравитация действует во многих пространственных измерениях, поэтому в нашем трехмерном мире она очень слаба. Чтобы доказать это утверждение, надо измерить константу G_N на малых расстояниях. Если существует 2 дополнительных измерения, надо измерять константу на расстояниях ~ 1 мм или еще меньших.
    Существует гипотеза: при энергиях LHC (шкала ТэВных энергий) гравитационные эффекты, могут сравниться с электромагнитными и слабыми. В основе этих рассуждений лежит новая гипотеза: фундаментальная энергетическая шкала − это Fermi-шкала (электрослабая шкала), а не Planck-шкала.

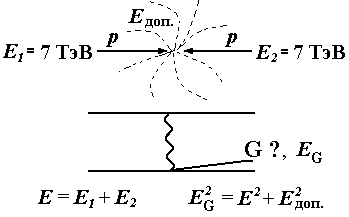Рис. 36. Схематическое изображение возможных эффектов выноса энергии E_доп (пунктирные линии) при столкновении протонов на LHC. Вынос энергии предположительно может быть осуществлен гравитоном G.

При этом возможна генерация гравитонов в соударениях протонов (7 ТэВ × 7 ТэВ) (рис. 36), причем гравитоны будут генерироваться столь же обильно, как фотоны, но, в отличие от фотонов, гравитоны будут уносить энергию в дополнительные измерения. Если таковые существуют, то будет наблюдаться энергии в нашем трехмерном пространстве.
На ускорителе LHC (ЦЕРН) планируются эксперименты по поиску гравитонов в соударениях протонов высокой энергии.

Литература

THE EUROPEAN PHYSICAL JOURNAL C. Particles and Fields. Zietschrift fur Pliysik C. v.15, No.1-4, 2000. Springer.
Мурзин B.C., Сарычева Л.И. Взаимодействия адронов высоких энергий. -М.: Наука, 1983.
Мурзин B.C., Сарычева Л.И. Физика адронных процессов. -М.: Энергоатомиздат, 1986.

4. Результаты измерения поперечных сечений разных типов взаимодействий