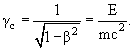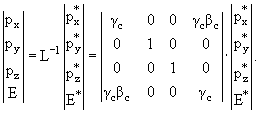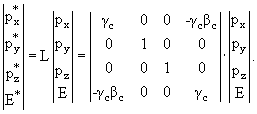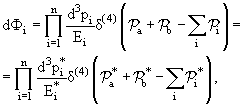Единицы измерения физических величин при описании явлений,
происходящих в микромире, подразделяются на основные и производные, которые
определяются через математическую запись законов физики.
В связи с тем, что все физические явления происходят в
пространстве и времени, за основные единицы принимают в первую очередь единицы
длины и времени, к ним присоединяется единица массы. Основные единицы: длины l, времени t, массы m −
получают определенную размерность. Размерности производных единиц определяются
формулами, выражающими определенные физические законы.
Размеры основных физических единиц
подбирают так, чтобы на практике было удобно ими пользоваться.
В системе СИ приняты следующие
размерности: длины [l] = м (метр), времени [t]
= с (секунда), массы [т] = кг (килограмм).
В системе СГС для основных единиц приняты следующие размерности: длины [/] =
см (сантиметр), времени [t] = с (секунда) и массы [т] = г (грамм). Для описания
явлений, происходящих в микромире, можно использовать обе системы единиц СИ и СГС.
Оценим порядки величин длины, времени и массы в явлениях микромира.
Кроме общепринятых международных систем единиц СИ и СГС используются также
"естественные системы единиц", опирающиеся на универсальные физические
константы. Эти системы единиц особенно уместны и используются в различных
физических теориях. В естественной системе единиц за основные единицы приняты
фундаментальные постоянные: скорость света в вакууме − с, постоянная Планка − ћ,
гравитационная постоянная GN, постоянная Больцмана − k: число
Авогадро − NA, и
др. В естественной системе единиц Планка принято с = ћ = GN = k = 1. Этой
системой единиц пользуются в космологии для описания процессов, в которых
одновременно существенны квантовые и гравитационные эффекты (теории Черных дыр,
теории ранней Вселенной).
В естественной системе единиц решена проблема естественной единицы длины.
Таковой можно считать комптоновскую длину волны λ0, которая определяется массой
частицы М: λ0 = ћ/Мс.
Длина характеризует размер объекта. Так, для электрона классический радиус
r0 = e2/mec2 = 2.81794·10-13 см (е, mе − заряд и масса электрона). Классический радиус
электрона имеет смысл радиуса заряженного шара с зарядом е (распределение
сферически симметрично), при котором энергия электростатического поля шара ε = γе2/r0 равна энергии покоя электрона
mec2 (используется при рассмотрении томпсоновского рассеяния света).
Используется также радиус боровской орбиты. Он определяется как расстояние от
ядра, на котором с наибольшей вероятностью можно обнаружить электрон в
невозбужденном атоме водорода
a0 = ћ2/mee2 (в СГС-системе) и
a0 = (α/4π)R =
0.529·10-10 м (в СИ-системе), α = 1/137.
Размер нуклона r ≈ 10-13 см (1 фемтометр). Характерные размеры атомных систем
− 10-8, ядерных систем − 10-12 ÷ 10-13 см.
Время изменяется в широком интервале и определяется как отношение расстояния R к скорости объекта v. Для микрообъектов τяд = R/v = 5·10-12
см/109 см/с ~ 5·10-22 с;
τэлем ч = 10-13
см/3·1010 см/с = 3·10-24 с.
Массы объектов изменяются от 0 до М. Так, масса электрона mе ≈ 10-27 г, масса
протона
mр ≈ 10-24 г (СГС-система). Одна атомная единица массы, использующаяся в
атомной и ядерной физике, 1 а.е.м. = М(С)/12 в единицах массы атома углерода.
К фундаментальным характеристикам микрообъектов следует отнести электрический
заряд, а также характеристики, необходимые для идентификации элементарной
частицы.
Электрический заряд частиц Q измеряется обычно в единицах заряда электрона.
Заряд электрона е = 1.6·10-19 кулон. Для частиц в свободном
состоянии Q/e = ±1, 0, а для кварков, входящих в состав адронов, Q/e = ±2/3 и
±1/3.
В ядрах заряд определяется количеством протонов Z, содержащихся в ядре.
Заряд протона по абсолютной величине равен заряду электрона.
Для идентификации элементарной частицы необходимо знать:
I − изотопический спин;
J − собственный момент количества движения − спин;
Р − пространственную четность;
С − зарядовую четность;
G − G-четность.
Эти сведения записываются в виде формулы IG(JPC).
Спин − одна из важнейших характеристик частицы, для измерения которой
используется фундаментальная константа Планка h или ћ = h/2π = 1.0544·10-27 [эрг-с].
Бозоны имеют целый спин в единицах ћ: (0,1, 2,...)ћ, фермионы − полуцелый (1/2,
3/2,.. .)ћ. В классе суперсимметричных частиц значения спинов фермионов и
бозонов меняются местами.
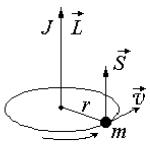 Рис- 4. Классическое представление момента количества движения J. |
Рис. 4 иллюстрирует физический смысл спина J по аналогии с классическим
представлением о моменте количества движения частицы с массой m = 1 г, движущейся со скоростью v = 1 см/с по окружности с радиусом
r = 1 см. В
классической физике момент количества движения J = mvr = L (L − орбитальный
момент). В квантовой механике J = [![]()
![]() ] = 1027ћ = 1 эрг·с для тех же параметров движущегося по окружности объекта, где ћ = 1.05·10-27 эрг·с.
] = 1027ћ = 1 эрг·с для тех же параметров движущегося по окружности объекта, где ћ = 1.05·10-27 эрг·с.
Проекция спина элементарной частицы на направление ее импульса называется
спиральностью. Спиральность безмассовой частицы с произвольным спином принимает
только два значения: по или против направления импульса частицы. Для фотона
возможные значения спиральности равны ±1, для безмассового нейтрино спиральность
равна ±1/2.
Спиновый момент количества движения атомного ядра определяется как векторная
сумма спинов элементарных частиц, образующих квантовую систему, и орбитальных
моментов этих частиц, обусловленных их движением внутри системы. Орбитальный
момент |![]() |, и спиновый момент
|
|, и спиновый момент
|![]() | приобретают дискретное значение. Орбитальный
момент |
| приобретают дискретное значение. Орбитальный
момент |![]() | = ћ[l(l
+1)]1/2, где l − орбитальное квантовое число (может принимать значения 0,
1,2,...), собственный момент количества движения |
| = ћ[l(l
+1)]1/2, где l − орбитальное квантовое число (может принимать значения 0,
1,2,...), собственный момент количества движения |![]() | = ћ[s(s
+ 1)]1/2 где s −
спиновое квантовое число (может принимать нулевые, целые или полуцелые значенияJ, полный момент количества движения равен сумме
| = ћ[s(s
+ 1)]1/2 где s −
спиновое квантовое число (может принимать нулевые, целые или полуцелые значенияJ, полный момент количества движения равен сумме
![]() +
+
![]() =
=
![]() .
.
К производным единицам следует отнести: энергию частицы, быстроту, заменяющую
скорость для релятивистских частиц, магнитный момент и др.
Энергия покоящейся частицы:
Е = mc2; движущейся частицы: Е = m2c4 + p2c2.
Для нерелятивистских частиц: Е = mс2 + р2/2m; для релятивистских частиц, с
массой m = 0: Е = ср.
Единицы измерения энергии − эВ, кэВ, МэВ, ГэВ, ТэВ, ... 1 ГэВ = 109 эВ, 1 ТэВ
= 1012 эВ,
1 эВ = 1.6·10-12 эрг.
Скорость частицы β = v/c, где с = 3·1010 см/с
− скорость света. Скорость
частицы определяет такую важнейшую характеристику как Лоренц-фактор частицы γ =
1/(1-β2)1/2 = E/mc2. Всегда γ > 1- Для нерелятивистских частиц 1 < γ < 2, а для релятивистских частиц γ > 2.
В физике высоких энергий скорость частицы β близка к 1 и для релятивистских
частиц ее трудно определить. Поэтому вместо скорости используется быстрота y, которая связана со скоростью соотношением у =
(1/2)ln[(1+β)/(1-β)] = (1/2)ln[(E+p)/(E-p)]. Быстрота
изменяется от 0 до ∞.
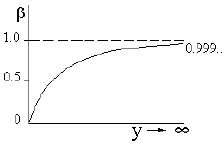 Рис. 5. Функциональная связь между скоростью частицы β и быстротой у. |
Функциональная связь между скоростью частицы и быстротой показана на рис. 5.
Для релятивистских частиц при β → 1, Е → р, тогда вместо быстроты можно
использовать псевдобыстроту η, которая определяется углом вылета частицы θ, η =
(1/2)ln tan(θ/2). В отличие от скорости быстрота − аддитивная величина, т.е. у2 = y0 + y1
для любой системы отсчета и для любых релятивистских и нерелятивистских частиц.
Магнитный момент μ = Iπr2/c, где ток
I = ev/2πr, возникает из-за вращения
электрического заряда. Таким образом, любая заряженная частица имеет магнитный
момент. При рассмотрении магнитного момента электрона используется магнетон Бора
μB =
eћ/2mec = 0.5788·10-14 МэВ/Гс, магнитный момент электрона
![]() = g·μB·
= g·μB·![]() . Коэффициент
g называется гиромагнитным отношением. Для электрона g =
. Коэффициент
g называется гиромагнитным отношением. Для электрона g =
![]() /μB·
/μB·![]() = 2, т.к. J = ћ/2,
= 2, т.к. J = ћ/2,
![]() = μB при условии, что электрон
− точечная бесструктурная
частица. Гиромагнитное отношение g содержит информацию о структуре частицы.
Величина (g − 2) измеряется в экспериментах, направленных на изучение структуры
частиц, отличных от лептонов. Для лептонов эта величина свидетельствует о роли
более высоких электромагнитных поправок (см. далее п. 7.1).
= μB при условии, что электрон
− точечная бесструктурная
частица. Гиромагнитное отношение g содержит информацию о структуре частицы.
Величина (g − 2) измеряется в экспериментах, направленных на изучение структуры
частиц, отличных от лептонов. Для лептонов эта величина свидетельствует о роли
более высоких электромагнитных поправок (см. далее п. 7.1).
В ядерной физике используется ядерный магнетон μя = eћ/2mpc, где mp − масса протона.
2.1.1. Система Хэвисайда и ее связь с системой СГС
В системе Хэвисайда скорость света с и постоянная Планка ћ полагаются равными единице, т.е. с = ћ = 1. Основными единицами измерения являются энергетические единицы − МэВ или МэВ-1, в то время как в системе СГС основные единицы измерения − [г, см, с]. Тогда, воспользовавшись соотношениями: Е = mc2 = m = МэВ, l = ћ/mc = МэВ-1, t = ћ/mc2 = МэВ-1, получим связь между системой Хэвисайда и системой СГС в виде:- m(г) = m(МэВ)·2·10-27,
- l (см) = l(МэВ-1)·2·10-11,
- t (с) = t (МэВ-1)·б.б·10-22.
Система Хэвисайда применяется в физике высоких энергий для описания явлений,
происходящих в микромире, и основана на использовании естественных констант с и
ћ, которые являются определяющими в релятивистской и квантовой механике.
Числовые значения соответствующих величин в системе СГС для электрона и
протона приводятся в табл. 3 и могут быть использованы для перехода из одной системы в другую.
Таблица 3. Числовые значения величин в системе СГС для электрона и протона
| Величины | Электрон | Протон |
| Длина, ћ/mc | 3.862·10-11 см | 2.103·10-14 см |
| Время ћ/mc2 | 1.288·10-21 с | 7.015·10-25 с |
| Масса m | 9.109·10-28 г | 1.6726·10-24 г |
| Энергия mс2 | 8.187·10-7 эрг 0.511 МэВ |
1.503·10-3 эрг 938.26 МэВ |
2.1.2. Планковские (естественные) единицы
При рассмотрении гравитационных эффектов для измерения энергии, массы, длины и времени вводится планковская шкала. Если гравитационная энергия объекта равна его полной энергии, т.е.
![]()
![]()
то
длина
![]() = 1.6·10-33 см,
= 1.6·10-33 см,
масса
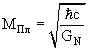 = 2.2 ·10-5 г = 1.2·1019 ГэВ,
= 2.2 ·10-5 г = 1.2·1019 ГэВ,
время
![]() = 5.4·10-44 с,
= 5.4·10-44 с,
где
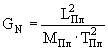 = 6.67·10-8 см2·г-1·с-2.
= 6.67·10-8 см2·г-1·с-2.
Гравитационные эффекты существенны, когда гравитационная энергия объекта сравнима с его полной энергией.
2.2. Классификация элементарных частиц
Понятие "элементарная частица" сформировалось с установлением дискретного характера строения вещества на микроскопическом уровне.
Атомы → ядра → нуклоны → партоны (кварки и глюоны)
В современной физике термин "элементарные частицы" употребляется для
наименования большой группы мельчайших наблюдаемых частиц материи. Эта группа
частиц весьма обширна: протоны р, нейтроны
n, π- и K-мезоны, гипероны,
очарованные частицы (J/ψ...) и множество резонансов (всего
~ 350 частиц). Эти
частицы получили название "адроны".
Выяснилось, что эти частицы не элементарны, а представляют собой составные
системы, конституентами которых являются истинно элементарные или, как их стали
называть, "фундаментальные" частицы −
партоны, открытые при изучении
структуры протона. Изучение свойств партонов позволило отождествить их с
кварками и
глюонами, введенными в рассмотрение Гелл-Манном и Цвейгом при
классификации наблюдаемых элементарных частиц. Кварки оказались фермионами со
спином J = 1/2. Им были приписаны дробные электрические заряды и барионное
число В = 1/3 поскольку барион, у которого В = 1, состоит из трех кварков. Кроме
того, для объяснения свойств некоторых барионов возникла необходимость введения
нового квантового числа − цвета. Каждый кварк имеет три цветовых состояния,
обозначаемые индексами 1, 2, 3 или словами красный (R), зеленый (G) и синий (В).
Цвет никак не проявляет себя у наблюдаемых адронов и работает только внутри них.
К настоящему времени открыто 6 ароматов (типов) кварков.
В табл. 4 приведены свойства кварков для одного цветового состояния.
Таблица 4. Свойства кварков
| Аромат | Масса, МэВ/с2 | I | I3 | Qq/e | s | с | b | t |
| u up | 330; (5) | 1/2 | 1/2 | 2/3 | 0 | 0 | 0 | 0 |
| d down | 340; (7) | 1/2 | -1/2 | -1/3 | 0 | 0 | 0 | 0 |
| s strange | 450; (150) | 0 | 0 | -1/3 | -1 | 0 | 0 | 0 |
| с charm | 1500 | 0 | 0 | 2/3 | 0 | 1 | 0 | 0 |
| b beauty | 5000 | 0 | 0 | -1/3 | 0 | 0 | -1 | 0 |
| t truth | 174000 | 0 | 0 | 2/3 | 0 | 0 | 0 | 1 |
Для каждого аромата кварка указаны его масса (приводятся массы конституентных
кварков и в скобках массы токовых кварков), изотопический спин I и 3-я проекция изотопического спина
I3, заряд кварка Qq/e и квантовые числа s, с, b, t. Наряду
с этими квантовыми числами часто используется квантовое число гиперзаряд Y = В +
s + с + b+ t. Существует связь между проекцией
изотопического спина I3,
электрического заряда Q и гиперзаряда Y: Q = I3 + (1/2)Y.
Поскольку каждый кварк имеет 3 цвета, в рассмотрении должны участвовать 18
кварков. Кварки не имеют структуры.
Вместе с тем, среди элементарных частиц оказался целый класс частиц,
получивших название "лептоны". Они
также являются фундаментальными частицами, т.е. не имеют структуры. Их шесть:
три заряженных е, μ, τ и три нейтральных νe, νμ,
ντ. Лептоны участвуют только в электромагнитных и слабых взаимодействиях.
Лептоны и кварки с полуцелым спином J = (n+1/2)ћ, n = 0, 1,... . относятся к
фундаментальным фермионам. Наблюдается удивительная симметрия между лептонами и
кварками: шесть лептонов и шесть кварков.
В табл. 5 приведены свойства фундаментальных фермионов: электрический заряд
Qi в единицах заряда электрона и масса частиц m. Лептоны и кварки объединяются в
три поколения (I, II и III). Для каждого поколения сумма электрических зарядов ∑Qi = 0 с учетом 3 цветовых зарядов у каждого кварка. Каждому фермиону
сответствует антифермион.
Кроме характеристик частиц, указанных в таблице, важную роль для лептонов
играют лептонные числа: электронное Le, равное +1 для е- и νe, мюонное Lμ,
равное +1 для μ- и νμ и таонное Lτ, равное +1 для τ-и ντ, которые соответствуют
ароматам лептонов, участвующих в конкретных реакциях, и являются сохраняющимися
величинами. Для лептонов барионное число В = 0.
Таблица 5. Свойства фундаментальных фермионов
| Частицы | Лептоны | Кварки | ||
| Электрический заряд, Qi | 0 | -1 | -1/3 | 2/3 |
|
I поколение m |
νe < 17 эВ/с2 |
е- 0.511 МэВ/с2 |
d 0.34 ГэВ/с2 |
u 0.33 ГэВ/с2 |
|
II поколение m |
νμ < 270 эВ/с2 |
μ- 105.7 МэВ/с2 |
s 0.45 ГэВ/с2 |
c 1.5 ГэВ/с2 |
|
III поколение m |
ντ < 35 МэВ/с2 |
τ- 1784 МэВ/с2 |
b 4.9 ГэВ/с2 |
t 175 ГэВ/с2 |
Окружающее нас вещество состоит из фермионов первого поколения ненулевой
массы. Влияние частиц второго и третьего поколений проявилось в ранней
Вселенной. Среди фундаментальных частиц особую роль играют фундаментальные калибровочные
бозоны, имеющие целочисленное внутреннее квантовое число спин J = nћ, n = 0, 1,
.... Калибровочные бозоны ответственны за четыре типа фундаментальных
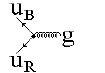
взаимодействий: сильное (глюон g), электромагнитное (фотон γ), слабое (бозоны
W±, Z0), гравитационное (гравитон G). Они также являются бесструктурными,
фундаментальными частицами.
В табл. 6 приведены свойства фундаментальных бозонов, являющихся полевыми
квантами в калибровочных теориях.
Таблица 6. Свойства фундаментальных бозонов
| Название | Заряд | Масса | Спин | Взаимодействия |
| Гравитон, G | 0 | 0 | 2 | Гравитационное |
| Фотон, γ | 0 | < 3·10-27 эВ | 1 | Электромагнитное |
| Заряженные векторные бозоны, W± | ±1 | 80.419 ГэВ/с2 | 1 | Слабое |
| Нейтральный векторный бозон, Z0 | 0 | 91.188 ГэВ/с2 | 1 | Слабое |
| Глюоны, g1, ... , g8 | 0 | 0 | 0 | Сильное |
| Хиггсы, Н0, H± | 0 | > 100 ГэВ/с2 | 0 |
Помимо свойств открытых калибровочных бозонов γ,
W±, Z0, g1,... , g8
в таблице
показаны свойства неоткрытых пока бозонов: гравитона G и Хиггс-бозонов Н0,
H±.
Рассмотрим теперь наиболее многочисленную группу элементарных
сильновзаимодействующих частиц − адронов, для объяснения структуры которых было
введено представление о кварках.
Адроны подразделяются на мезоны и барионы. Мезоны построены из кварка и антикварка (q![]() ). Барионы состоят из трех кварков (q1q2q3).
). Барионы состоят из трех кварков (q1q2q3).
В табл. 7 приводится перечень свойств основных адронов. (Подробные таблицы см. The European Physical Journal C, Rev. of Particle
Phys., v.15, №1 - 4, 2000.)
Таблица 7. Свойства адронов
| Название | Масса, МэВ/с2 | Время жизни, с | Моды распада | Кварковый состав | ||||||||||||||||||||
|
м е з о н ы
|
Пион
π± 1-(0-+) π0 |
139.567 134.965 |
2.6·10-8 |
π± → μ± + ν π0 → γ + γ |
(u (u | |||||||||||||||||||
|
η-мезон η0 0+(0-+) |
548.8 | Г=1.18±0.11 кэВ |
η0 → γ + γ; 3π0 →π+ + π-0 + π-- |
с1(u | ||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||
|
D± D0 |
1869.3 1864.5 |
10.69·10-13 4.28·10-13 |
D± → е± + X |
(c (c | ||||||||||||||||||||
|
F± =
|
1969.3 | 4.36·10-13 |
|
(c | ||||||||||||||||||||
|
B± В0 |
5277.6 5279.4 |
13.1·10-13 13.1·10-13 |
B± → В0 → |
(u (d | ||||||||||||||||||||
| б а р и о н ы |
Протон р Нейтрон n |
938.3 939.5 |
> 1033 лет 898 ±16 |
n → р + е-+ |
uud udd | |||||||||||||||||||
| Λ |
1115.6 |
2.63·10-10 | Λ→p + π- | uds | ||||||||||||||||||||
|
Σ+ Σ0 Σ- |
1189.4 1192 1197 |
0.8·10-10 5.8·10-20 1.48·10-10 |
Σ+→p
+ π0 Σ0 → Λ+ γ Σ- →n + π- |
uus uds dds | ||||||||||||||||||||
|
Ξ0 Ξ- |
1314.9 1321 |
2.9·10-10 1.64·10-10 |
Ξ0 → Λ+ π0 Ξ- → Λ + π- |
uss dss | ||||||||||||||||||||
| Ω- | 1672 | 0.8·10-10 | Ω-→ Λ+ K- | sss | ||||||||||||||||||||
|
|
|
|
|
Кварковая структура адронов позволяет выделить в этой многочисленной группе
частиц нестранные адроны, которые состоят из нестранных кварков (и, d), странные
адроны, в состав которых входит странный кварк s, чармированные адроны,
содержащие с-кварк, прелестные адроны (боттом-адроны) с b-кварком.
В таблице представлены свойства только незначительной части адронов: мезонов
и барионов. Показаны их масса, время жизни, основные моды распада и кварковый
состав. Для мезонов барионное число В = О и лептонное число L = 0. Для барионов
барионное число В = 1, лептон-ное число L = 0. Мезоны относятся к бозонам (целый
спин), барионы − к фермионам (спин полуцелый).
Дальнейшее рассмотрение свойств адронов позволяет объединить их в
изотопические мультиплеты, состоящие из частиц с одинаковыми квантовыми числами
(барионным числом, спином, внутренней четностью, странностью) и близкими по
значению массами, но с различными электрическими зарядами. Каждый изотопический
мультиплет характеризуется изотопическим спином I, который определяет полное
число частиц, входящих в мультиплет, равное 2I
+ 1. Изоспин может принимать
значения 0, 1/2, 1, 3/2, 2, . .., т.е. возможно существование изотопических
синглетов, дублетов, триплетов, квартетов и т.д. Так, протон и нейтрон
составляют изотопический дублет, π+-, π--, π0-мезоны рассматриваются как
изотопический триплет.
Более сложными объектами в микромире являются атомные ядра. Атомное ядро
состоит из Z протонов и N нейтронов. Сумма Z + N = А − число нуклонов в данном
изотопе. Часто в таблицах приводится усредненная по всем изотопам величина,
тогда она становится дробной. Известны ядра, для которых указанные величины
находятся в пределах: 1 < А < 289, 1 < Z < 116.
Перечисленные выше частицы рассматриваются в рамках Стандартной Модели.
Предполагается, что за пределами Стандартной Модели может существовать еще одна
группа фундаментальных частиц − суперсимметричные частицы (SUSY). Они должны
обеспечить симметрию между фермионами и бозонами. В табл. 8 приводятся
предполагаемые свойства этой симметрии.
Таблица 8. Свойства суперсимметричных частиц
| Частица | Спин J |
Частица суперсимметричная |
Спин J | ||||||||||||||||||||
|
Кварк q Лептон l |
1/2 1/2 |
Скварк
Слептон |
0 0 | ||||||||||||||||||||
|
|
|
|
Появляется новое квантовое число:
R = 3B + L + 2 J,
В − барионное число, L − лептонное число, J − спин.
Для обычных частиц R = +1, для суперсимметричных частиц R = -1.
До сих пор суперсимметричные частицы в экспериментах не обнаружены.
2.3. Полевой подход к проблеме взаимодействий
2.3.1 Свойства фундаментальных взаимодействий
Огромное многообразие физических явлений, происходящих при столкновениях
элементарных частиц, определяется всего лишь четырьмя типами взаимодействий:
электромагнитным, слабым, сильным и гравитационным. В квантовой теории
взаимодействие описывается в терминах обмена специфическими квантами (бозонами),
ассоциированными с данным типом взаимодействия.
Для наглядного представления взаимодействия частиц американский физик
Р. Фейнман предложил использовать диаграммы, которые получили его имя. Диаграммы
Фейнмана описывают любой процесс взаимодействия при столкновении двух частиц.
Каждая частица, участвующая в процессе, на диаграмме Фейнмана изображается
линией. Свободный левый или правый конец линии обозначает нахождение частицы в
начальном или конечном состоянии соответственно. Внутренние линии на диаграммах
(т.е. линии, не имеющие свободных концов) соответствуют так называемым
виртуальным частицам. Это частицы, рождающиеся и поглощающиеся в процессе
взаимодействия. Их нельзя зарегистрировать, в отличие от реальных частиц.
Взаимодействие частиц на диаграмме изображается узлами (или вершинами). Тип
взаимодействия характеризуется константой связи α которая может быть записана в
виде: α = g2/ћc, где
g − заряд источника взаимодействия, а является основной
количественнои характеристикой силы, действующей между частицами. В
электромагнитном взаимодействии αе = e2/ћc
=
1/137.
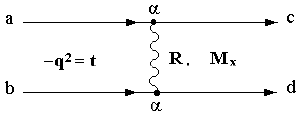 Рис.6. Диаграмма Фейнмана. |
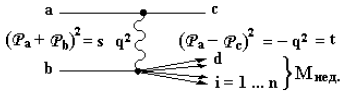
Процесс a +
b →с + d
в виде диаграммы Фейнмана (рис. 6) выглядит следующим образом: R − виртуальная частица, которой обмениваются
частицы а и b при взаимодействии, определяемом
константой взаимодействия
Виртуальная частица может иметь массу Мх и при обмене этой частицей
происходит передача 4-импульса t = −q2 = Q2.
В табл. 9 представлены характеристики разных типов взаимодействий.
Электромагнитные взаимодействия. Наиболее полно и последовательно изучены
электромагнитные взаимодействия, которым подвержены все заряженные частицы и
фотоны. Переносчиком взаимодействия является фотон. Для электромагнитных сил
константа взаимодействия численно равна постоянной тонкой структуры αе = e2/ћc =
1/137.
Примерами простейших электромагнитных процессов являются фотоэффект,
комптон-эффект, образование электрон-позитронных пар, а для заряженных частиц −
ионизационное рассеяние и тормозное излучение. Теория этих взаимодействий −
квантовая электродинамика − является наиболее точной физической теорией.
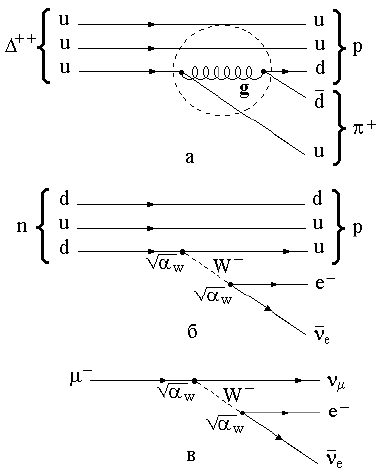
Слабые взаимодействия. Впервые слабые взаимодействия наблюдались при β-распаде атомных ядер. И, как оказалось, эти распады связаны с превращениями
протона в нейтрон в ядре и обратно:
р → n + е+ + νe, n → р + е- +
![]() e.
Возможны и обратные реакции: захват электрона е- + р → n + νe или антинейтрино
e.
Возможны и обратные реакции: захват электрона е- + р → n + νe или антинейтрино
![]() e + р → е+ +
n. Слабое взаимодействие было описано Энрико Ферми в 1934 г. в
терминах четырехфермионного контактного взаимодействия, определяемого константой
Ферми
e + р → е+ +
n. Слабое взаимодействие было описано Энрико Ферми в 1934 г. в
терминах четырехфермионного контактного взаимодействия, определяемого константой
Ферми
GF = 1.4·10-49 эрг·см3.
При очень высоких энергиях вместо фермиевского контактного взаимодействия
слабое взаимодействие описывается как обменное, при котором осуществляется обмен
квантом, наделенным слабым зарядом gw (по аналогии с электрическим зарядом) и
действующим между фермионами. Такие кванты были впервые обнаружены в 1983 г. на
SppS-коллайдере (ЦЕРН) коллективом под руководством Карла Руббиа. Это заряженные
бозоны − W± и нейтральный бозон − Z0, их массы соответственно равны: mW± = 80 ГэВ/с2
и mZ = 90 ГэВ/с2. Константа взаимодействия αW в этом случае выражается через
константу Ферми:
![]()
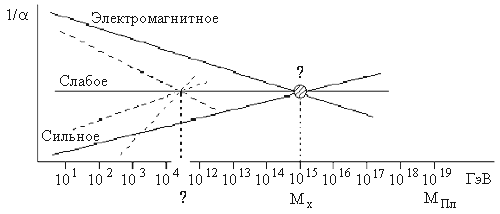
Таблица 9. Основные типы взаимодействий и их характеристики
 r <
rp
r <
rp

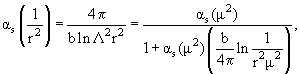
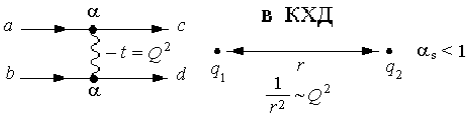
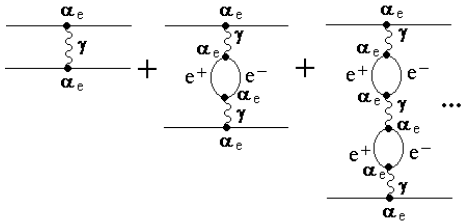
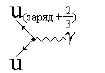
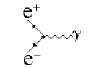
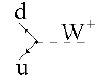
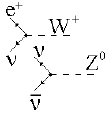
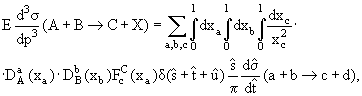
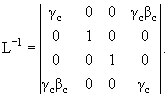
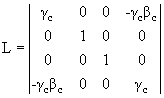 − матрица перехода.
− матрица перехода.