Бозоны W и Y можно ввести как калибровочные поля, что
обеспечивает перенормируемость теории электрослабых взаимодействий. Мы уже
познакомились с методом построения лагранжианов, инвариантных относительно
локальных калибровочных преобразований, на примере электромагнитного поля и
изотриплета полей векторных ρ-мезонов.
Мы уже ввели понятие слабого изоспина, а теперь потребуем
локальной калибровочной инвариантности лагранжиана левоспиральных и
правоспиральных кварковых (и лептонных) полей относительно преобразований в
слабом изотопическом пространстве по группе SU(2)Lx SU(1).
При этом мы, рассматривая отдельно лево- и правоспиральные
компоненты кварков (и лептонов), положим их массы раными нулю.
Достаточно написать выражение для одного левоспирального
слабого изодублета и соответствующих правоспиральных слабых изосинглетов uR,
dR:
L0 = 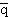 L(x)∂μγμqL(x)
+ L(x)∂μγμqL(x)
+  R(x)∂μuR(x)
+ R(x)∂μuR(x)
+ 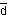 R(x)∂μdR(x). R(x)∂μdR(x). |
(5.23) |
Этот лагранжиан инвариантен относительно глобального калибровочного
преобразования
q'L(x) = 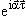 qL(x),
qL(x),
u'R,L(x) = 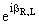 uR,L(x),
uR,L(x),
d'R,L(x) =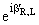 dR,L(x),
dR,L(x),
где матрицы 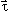 действуют в
слабом изотопическом пространстве, а
действуют в
слабом изотопическом пространстве, а 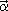 = (
= ( 1,
1,  2,
2,  3),
3), 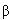 R,L,
R,L,
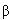 'R,L
- произвольные вещественные фазы.
'R,L
- произвольные вещественные фазы.
Потребуем теперь инвариантности лагранжиана относительно
подобного, но локального калибровочного преобразования, когда
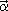 и
и 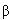 R,L,
R,L, 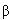 'R,L
являются функцией x: Но, как и в предыдущем случае, L0
неинвариантен относительно подобного локального калибровочного преобразования:
'R,L
являются функцией x: Но, как и в предыдущем случае, L0
неинвариантен относительно подобного локального калибровочного преобразования:
Для того, чтобы убрать члены, нарушающие калибровочную инвариантность, введем
слабый изотриплет векторных полей 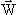 μи
слабый изосинглет Yμс
калибровочными преобразованиями
μи
слабый изосинглет Yμс
калибровочными преобразованиями
где U = 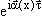 ;
;
Y'μ= Yμ
- 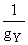
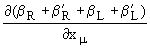 .
.
Взаимодействие этих полей с кварками зададим лагранжианом, который мы уже
построили выше
Итак, требование инвариантности лагранжиана относительно локальных
калибровочных преобразований по группе SU(2)L×SU(1)
приводит к появлению четырех безмассовых векторных полей 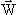 , Y.
, Y.
Ранее уже было показано, как поля с нулевым электрическим
зарядом W3μ,Yμортогональным
преобразованием переводятся в Zμ,
Aμ. Затем вводится механизм
спонтанного нарушения симметрии, который строится таким образом, чтобы поля W±,
Z оказались массивными, а поле Aμосталось
безмассовым. Это производится обычно с помощью так наз. механизма Хиггса. В
итоге, повторяя рассуждения для других ароматов, приходим к уже полученным
выражениям для заряженных и нейтральных токов, только уже в
калибровочно-инвариантной теории со спонтанным нарушением симметрии.

![]() μ.
На эксперименте этот распад подавлен почти на 7 порядков!!!
μ.
На эксперименте этот распад подавлен почти на 7 порядков!!!![]() c).
c).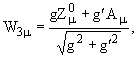
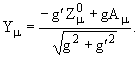
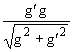 [(
[(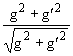
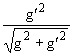 Jem
=
Jem
=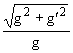 g
g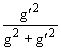 Jem.
Jem.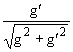 ,
cos
θW =
,
cos
θW = 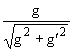 .
.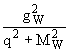
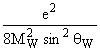 ,
,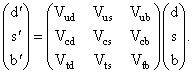
 .
.
 x
x