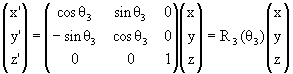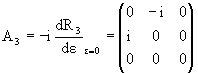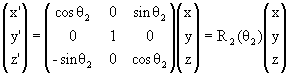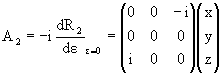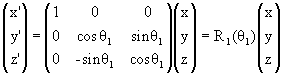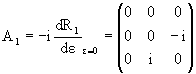©hoo$e ЛAнg?Age©///?Ang?Age® Ekohomei©A TALKiNg ?.?.м.?.

geo.rf.gd

   

1.2 Группы и алгебры. Основные понятия

    Определение группы

Пусть задано множество элементов G  g1, g2, ... , gn , обладающих следующими свойствами:

  1. Определен закон умножения элементов gi gj  =  gk, причем если gi, gj G, то gi gj = gk G, 
    i, j, l = 1, 2, ..., n.
  2. Выполняется закон ассоциативности gi (gj gk) = (gi gj) gk.
  3. Существует единичный элемент e, egi = gi, i = 1, 2, ... , n.
  4. Существует обратный элемент  g i-1, g i-1gi = e,  i = 1, 2, ... , n.

Тогда на множестве G задана группа элементов g1, g2, ... , gn

    В качестве простого примера рассмотрим вращение на плоскости. Зададим множество Ф всех поворотов на углы φ

  1. Закон умножения в данном случае - это сложение углов: φ1 + φ2 = φ3 Ф.
  2. Закон ассоциативности запишется как (φ1 + φ2) + φ3 = φ1 + (φ2 + φ3).
  3. Единичный элемент в данном случае - поворот на угол 0 ( +2πn ).
  4. Обратный элемент в данном случае -поворот на угол - φ(+2πn).

Итак, вращения вокруг оси, перпендикулярной выбранной плоскости, образуют группу.
    Рассмотрим поворот координатных осей  x, y, z, задающих декартову систему координат в 3-мерном пространстве, на угол θ3 в плоскости x y вокруг оси z:

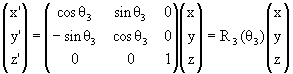
(1.1)

Пусть ε - бесконечно малый поворот. Разложим матрицу поворота R3(ε) в ряд Тэйлора и ограничимся членами, линейными по ε:

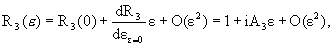
(1.2)

где использовано, что R3(0) суть единичная матрица, и введена матрица

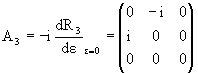
(1.3)

которую назовем генератором поворота вокруг 3-ей оси (оси z). Выберем ε = η3/n, тогда поворот на угол η3 получится n-кратным применением оператора R3(ε) , и в пределе

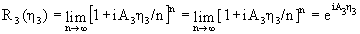
(1.4)

Рассмотрим повороты вокруг оси у:

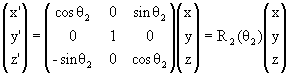
(1.5)

где, соответственно, введен генератор поворота вокруг оси  у:

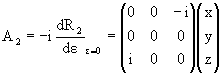
(1.6)

и вокруг оси x:

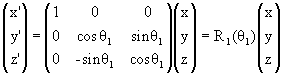
(1.7)

где введен генератор поворота вокруг оси x:

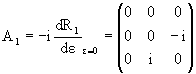
(1.8)

Теперь в трехмерном пространстве можно уже записать поворот декартовой 3-мерной системы координат на произвольные конечные углы, например, как

.

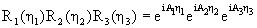(1.9)

Обычно, однако, вращение в 3-мерном пространстве задают несколько иначе, а именно, посредством углов Эйлера

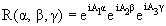
(1.10)

Генераторы Al  l = 1, 2, 3,   удовлетворяют коммутационным соотношениям

Ai·Aj - Aj·Ai = [Ai, Aj] = i εijk Ak,

(1.11)

где  εijk - абсолютно антисимметричный тензор 3-го ранга. Отметим,что матрицы Al  l = 1, 2, 3, антисимметричны, тогда как матрицы Rk-ортогональны, т.е. 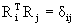, где значок  T означает транспонирование. Повороты могут быть полностью заданы посредством генераторов Al   l = 1, 2, 3, другими словами, группа 3-мерных вращений (как, впрочем, и любая непрерывная группа Ли с точностью до дискретных преобразований) вполне характеризуется заданием алгебры , т.е. заданием генераторов Al ,   l = 1, 2, 3, их линейных комбинаций и коммутационных соотношений.

    Определение  алгебры

L - алгебра Ли над полем вещественных чисел K, если:
(i) L -линейное пространство над К (для x L определено умножение  на числа из К),
(ii) для x,y L определен коммутатор  [x, y], также принадлежащий L, причем [x, y] обладает свойствами:
[альфаx, y] = альфа[x, y], [x, альфаy] = альфа[x, y] при альфа K и [x1 + x2, y] = [x1, y] + [x2, y],
[x, y1 + y2] = [x, y1] + [x, y2]   для всех x, y L;
[x, x] = 0  для всех x, y L;
[[x, y] z] + [[y, z] x] + [[z, x] y] = 0 (тождество Якоби).

Содержание Продолжение

На головную страницу
Top.Mail.Ru