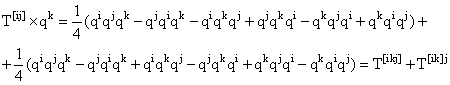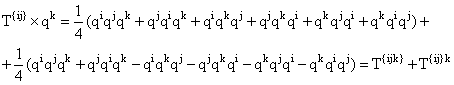Ассоциируя q^α со спиновыми функциями объекта со спином 1/2, причем и являются базисными спинорами с проекциями спина +1/2 и -1/2, соответственно, (это барионы спина 1/2 и кварки, как мы увидим позже), мы можем образовать симметричный тензор с тремя компонентами

и мы ввели 1/, чтобы нормировать эту компоненту на 1.
    Ассоциируя опять со спиновыми функциями объекта со спином 1/2, запишем единственную компоненту синглета в виде

и мы ввели 1/ для нормировки на единицу.
    Для примера образуем произведение спинора q^α и ему сопряженного спинора q_β с базисными спинорами в виде строк (1 0) и (0 1). Разложение в сумму НП достигается здесь вычитанием шпура (напомним, что матрицы Паули бесшпуровые)

где - бесшпуровый тензор размерности d_V =(n² - 1), соответствующий векторному представлению группы SU(2) и имеющий для n = 2 размерность 3; I - единичная матрица, соответствующая единичному представлению. Группа SU(2) так мала, что оба ее НП Т^{αβ} и соответствуют одному и тому же НП размерности 3, тогда как НП соответствует скалярному НП как и . Для n 2 это не так, как будет видно дальше.