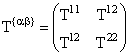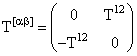Итак, познакомившись с группой 3-мерных вращений, в которой размерность минимального нетривиального (отличного от 1) представления равна 3, рассмотрим более сложную группу, в которой есть представление размерности 2. Для этого зададим совокупность 2 x 2 унитарных унимодулярных матриц U, т.е., U+U = 1, det U = 1. Такая матрица U может быть выражена в виде
U = |
(1.30) |
,
k, k = 1, 2, 3 -
эрмитовы матрицы, 
,
которые мы выбираем в виде матриц Паули
|
(1.31) |
, 
,а ak, k = 1, 2, 3 - произвольные вещественные
числа. Эти матрицы образуют группу с обычным
законом умножения матриц и реализуют
присоединенное или тождественное представление
размерности 2, натянутом на два базисных вектора.
Замечательно, что матрицы Паули
подчиняются тем же коммутационным соотношениям,
что и генераторы группы вращений O(3). Попытаемся
связать поэтому эти матрицы с обычным 3-мерным
вектором 
. Для этого
каждому вектору сопоставим величину 
, a,b = 1,2.
т.е.
определяет квадрат длины вектора. Взяв
совокупность унитарных унимодулярных матриц U , U+U
= 1, detU = 1 в 2-мерном пространстве, определим
Мы делаем вывод,
что преобразования U оставляют инвариантной
длину вектора и, стало быть, соответствуют
вращениям в 3-мерном пространстве, причем +U
соответствуют одному и тому же вращению.
Соответствующая алгебра SU(2) задается эрмитовыми
матрицами σk, k = 1,
2, 3, с коммутационными соотношениями
и 
можно разложить в прямую сумму двух
неприводимых представлений (НП) просто
симметризуя и антисимметризуя произведение:
и для n=2 
, что видно из матричного
представления:
и
для n = 2 
, что видно
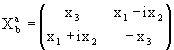из его матричного представления
(
12 = -
