А. Пайс и О. Пиччиони предсказали специфическую особенность взаимодействия K⁰-мезонов с ядрами - осцилляцию в пучке нейтральных K-мезонов.

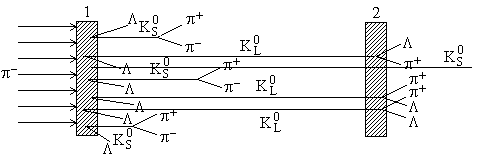
    Пучок π^--мезонов падает на мишень 1 (рис. 1), в которой в результате реакции

π⁻ + p → Λ + K⁰

образуются Λ-гипероны и K⁰-мезоны. В точке (1) вблизи мишени K⁰-мезоны представляют собой равную смесь состояний и

|K⁰> = |> = (|> + |>)/.

При движении вправо в волновой функции K⁰ компонента будет распадаться быстрее, чем , из-за разного времени жизни состояний и . При t >> τ() волновая функция будет представлять собой практически чистое состояние /, которое в свою очередь является суперпозицией состояний |K⁰> и |K⁰>

|>/ = (|K⁰> + |K⁰>)/2.

В результате взаимодействия пучка -мезонов со второй мишенью будет наблюдаться реакция

K⁰ + p → Λ + π⁺,

которая невозможна под действием K⁰-мезонов. Таким образом, в результате взаимодействия с мишенью, в пучке будет возрастать доля K⁰-мезонов (процесс регенерации).
    Динамику регенерации K⁰ и K⁰ в пучке можно описать следующим образом.

K(t) = [(t) + (t)],
(t) = exp[-iEt/-λ_Lt/2],
(t) = exp[-iEt/-λ_St/2],
K(0) = K⁰,

где λ_L и λ_S -постоянные распада и -мезонов.
    Учитывая, что

|> = (|K⁰> - |K⁰>)/,  |> = (|K⁰> + |K⁰>)/ и
E² = p²c² + m²c⁴,

после преобразования получим

K(t) = 1/2{K⁰[exp(im_Lt-λ_Lt/2) + exp(im_St-λ_St/2)] + K⁰[exp(im_St-λ_St/2) - exp(im_Lt-λ_Lt/2)].

Вероятности W(K⁰) и W(K⁰) наблюдения в момент t состояний K⁰ и K⁰

W(K⁰) = 1/4{exp(-λ_Lt) + exp(-λ_St) + 2exp[-t(λ_S+λ_L)/2]cosΔmt };
W(K⁰) = 1/4{exp(-λ_Lt) + exp(-λ_St) - 2exp[-t(λ_S+λ_L)/2]cosΔmt }.

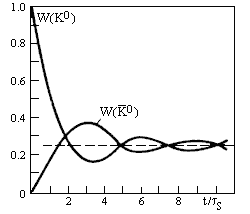
Зависимости  W(K⁰) и W(K⁰) от времени показана на рис. 2. По периоду осцилляции можно определить разность масс и  -мезонов.

m() - m() = (3.491 + 0.009)·10^-12 МэВ.