Исследования свойств нейтральных K⁰ и K⁰-мезонов представляет особый интерес, т.к. они позволяют изучить ряд уникальных проявлений принципов квантовой механики.

1. Линейные комбинации двух состояний также является состоянием системы. K⁰ и K⁰ можно представить как суперпозицию двух других состояний K₁ и K₂.
2. Распады K⁰ и K⁰-мезонов показали, что CP-симметрия не является точной симметрией.

    Нейтральные мезоны K⁰ и K⁰ являются частицей и античастицей. Они связаны процедурой зарядового сопряжения. Выберем фазы так, что Ĉ |К⁰> = -|K⁰> и Ĉ|K⁰> = -|К⁰>. Единственное квантовое число, которым различаются K⁰ и K⁰, - это странность (S(К⁰) = 1, S(K⁰) = -1). Поэтому обе частицы должны иметь одинаковые массы и одинаковые времена жизни. K⁰ имеет кварковую структуру d, а K⁰ - s. Они по-разному ведут себя в сильном взаимодействии. Так согласно закона сохранения странности в сильных взаимодействиях K⁰-мезоны могут образовываться в реакции

в то время как для K⁰-мезонов такая реакция запрещена

π− + p Λ+ K0, Δs = -2.

(2)

K⁰ в сильных взаимодействиях могут образовываться в реакции

π− + p n + K0 + K0

(3)

при более высоких энергиях. Распад К⁰ и K⁰-мезонов происходит в результате слабого взаимодействия. При этом наблюдается ситуация показанная схематически на рисунке.

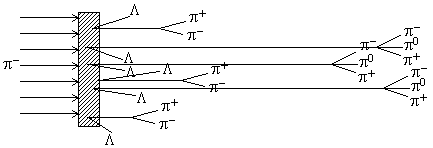Если пучком π⁻-мезонов обстреливать мишень, то в результате реакции (1) из мишени будут вылетать Λ-гипероны и K⁰-мезоны. Так как время жизни Λ-гиперона 2.6·10^-10 с, он распадается вблизи мишени на протон и ^--мезон.

Вблизи мишени наблюдаются и вилки π⁻π⁺ от распадов K⁰-мезонов

Однако такие распады наблюдаются лишь для 50% образовавшихся K⁰-мезонов. В оставшихся 50% случаев K⁰ распадается гораздо дальше от мишени на 3π-мезона.
Проанализируем выполнение закона сохранения комбинированной четности в распадах К⁰-мезонов на 2 и 3 π-мезона.
    Состояния К⁰ и K⁰ не имеют определенного значения СР-четности. Действие операторов СР на волновые функции К⁰ и K⁰ можно записать в виде:

Ĉ|К⁰> = -|K⁰>,  Ĉ|K⁰> = -|К⁰>, 
|К⁰> = -|К⁰>,    |K⁰> = -|K⁰>,
Ĉ |К⁰> = |K⁰>,  Ĉ|K⁰> = |К⁰>,

Однако из состояний К⁰ и K⁰ можно построить линейную комбинацию и , имеющую определенные значения СР-четности:

,
.

K₁ и K₂ не являются частицей и античастицей и поэтому могут иметь разные характеристики распада.
СР-четности состояний и

Ĉ |> =  +1|>,
Ĉ |> =  -1|>.

    Двухпионные π⁺π⁻ и трехпионные π⁺π⁻π⁰ системы при нулевом орбитальном моменте l являются собственными состояниями -оператора. Для двухпионной системы

π⁺π⁻ система, l = 0.

Операция P эквивалентна обмену π⁺π⁻-мезонов местами. При таком обмене волновая функция приобретает множитель(-1)^l.

|π⁺π⁻> = |π⁺> |π⁻> (-1)^l = +1 |π⁺π⁻>.

Операция C превращает π⁺ в π⁻ и π⁻ в π⁺, т.е. она тоже эквивалентна обмену обмену π⁺π^−--мезонов местами.

Ĉ |π⁺π⁻> =  (-1)^l|π⁺π⁻> = +1|π⁺π⁻>,
Ĉ |π⁺π⁻> =  (-1)^2l |π⁺π⁻> = |π⁺π⁻> .

Собственное значение Ĉ-оператора двухпионной системы (l = 0) равно +1.

Для трехпионной системы

π⁺π⁻⁰ система, l = 0.
|π⁺π⁻⁰> = |π⁺> |π⁻> |π⁰> (-1)^l = -1 |π⁺π⁻π⁰>,
Ĉ |π⁺π⁻π⁰> = |π⁺π⁻π⁰> (-1)^l = +1|π⁺π⁻π⁰>,
Ĉ |π⁺π⁻π⁰> =  -1|π⁺π⁻π⁰>.

Собственное значение -оператора трехпионной системы (l = 0) равно -1 .
Таким образом, состояния |> и |> имеют определенные значения CP-четности, но не имеют определенного значения странности s.
В свою очередь можно записать

|К⁰> = (|> + |>)/,
|K⁰> = (|> - |>)/.

Т.е. каждая из частиц K⁰ и K⁰ является суперпозицией состояний и . Т.к. CP() = +1, в соответствии с законом сохранения комбинированной четности, распадается на 2 π-мезона. Среднее время жизни состояния () ~ 0.9·10^-19 с. В свою очередь CP() = -1, поэтому распадается на 3 π-мезона, также без нарушения комбинированной четности. Время жизни должно быть больше времени жизни из-за меньшего фазового объема для продуктов распада
(τ() ~ 5·10^-8 с). Т.к. K⁰-мезон на 50% состоит из компоненты , то вблизи мишени наблюдаются распады этой компоненты на 2π-мезона. На большем растоянии от мишени наблюдается распад компоненты на 3π-мезона.
    В природе существует две линейно независимые комбинации состояний и , которые отвечают частицам с различными массами и средним временем жизни:

m(К⁰) = 497.67 МэВ
τ() = 5.2·10^-8 c,
τ() = 0.9·10^-10 c.

Основные каналы распада

Основные каналы распада

	π0π0π0	21.1%,
	π+π−-π0	12.6%
	π+−μ, π−+νμ	27.1%
	π+е−e, π−e+e	38.8%

Разность масс и

m() - m() =(3.491 + 0.009)·10^-12 МэВ.

Если бы СР-инвариантность имеет место, можно считать:

|>| ≡ |>,  |> ≡ |>.

Однако, в 1964 г. было обнаружено, что существует малая, но конечная вероятность распада:

  π⁺ + π^−-,

в котором собственное значение Ĉ-оператора в конечном состоянии, как мы уже показали, имеет СР = +1:

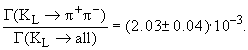
Этот результат означает, что нельзя отождествлять состояние с и с
    Вместо этого можно следующим образом определить состояния и

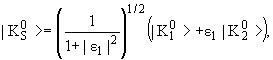
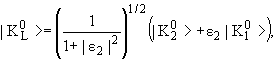
где ε₁ и ε₂ - малые комплексные числа.

18.01.17