Законы сохранения в ядерных реакциях
Общие закономерности применения законов сохранения к
реакциям были рассмотрены на семинаре 2. Там же была получена формула расчета
пороговой кинетической энергии падающей на неподвижную мишень частицы, при
которой возможна эндотермическая реакция (т.е. реакция с увеличением массы покоя
частиц в конечном состоянии Q = ![]() mi
-
mi
- ![]() mf < 0
).
mf < 0
).
|
(14.1) |
| Задача 14.1. Определить пороговую энергию а) б) |
Для частиц с массой покоя, равной 0, кинетические и полные энергии совпадают. Поэтому пороговая энергия гамма-кванта в реакции (а) равна (см. (2.18))
Tпор = [M(11C) + mn - M(12C)].
[M(11C) + mn + M(12C)]/2M(12C)
≈ Δ(11C) + Δn - Δ(12C)
=
= 10.65 + 8.07 - 0 = 18.72 МэВ.
(Величины избытков масс Δ можно найти в приложении к [4] и на сайте
ЦДФЭ (cdfe.sinp.msu.ru/services/gsp.en.html).
Аналогичный расчет для реакции протонного фоторасщепления (б) дает Tпор = 15.96 МэВ.
Ядерные реакции часто могут протекать по разным каналам реакции. Фотоядерные реакции, рассмотренные в этой задаче, при кинетических энергиях гамма-квантов выше, чем 18.72 МэВ, идут как по каналу (a), так и по каналу (б).
| Задача 14.2. Определить пороговую энергию протона в
реакции подхвата p + 13C |
Минимальная (пороговая) кинетическая энергия протона в реакции равна (см. (2.19))
![]()
![]() .
.
Во втором члене в скобках массы можно заменить массовыми числами, а третьим членом в нерелятивистском случае можно пренебречь.
![]()
Законы сохранения энергии, импульса, момента количества движения, барионного и электрического зарядов выполняются во всех реакциях. Закон сохранения барионного заряда проявляется в ядерных реакциях в виде закона сохранения числа нуклонов, что и было использовано при расчетах задач 14.1 и14.2 при переходе от полных масс М к избыткам масс Δ = М - А.
В ядерных реакциях, протекающих по сильным или электромагнитным взаимодействиям выполняется также закон сохранения Р-четности. Законы сохранения момента количества движения и Р-четности часто используют вместе для получения правил отбора.
| Задача 14.3. Определить возможные значения
орбитального момента дейтрона в реакции |
Закон сохранения момента импульса для данной реакции имеет
вид:
![]()
Закон сохранения Р- четности: (+1)(-1)=(+1)(+1)(-1)ld, поэтому
ld - нечетное.
Единственным решением, удовлетворяющим обоим законам сохранения является
ld=1.
В реакциях сильного взаимодействия выполняется также
закон сохранения изоспина. Использование этого закона при анализе ядерных
реакций является одним из способов идентификации значения изоспина.
| Задача 14.4. Какие состояния из приведенного на
схеме спектра ядра 14N могут быть
возбуждены в реакциях неупругого рассеяния |
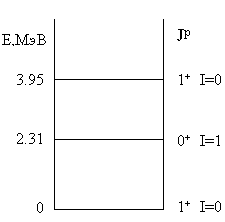
Анализ закона сохранения изоспина для реакций сильного взаимодействия
![]()
![]()
приводит к выводу, что уровень с изоспином 1 в этих реакциях не может быть
возбужден: 0 + 0 = 0 + I, I = 0.
Для реакции неупругого рассеяния протонов
![]()
возможно возбуждение как состояний с изоспином 0, так и состояний с изоспином 1:
0 + ![]() =
= ![]() +
+ ![]() ;
I = 0,1.
;
I = 0,1.
Сравнения спектров возбуждения ядра 14N в реакциях ![]() ,
,![]() ')
')
Характеристикой вероятностей протекания ядерных реакций является эффективное сечение реакции (см. семинар 2). Каждому каналу реакции соответствует свое эффективное сечение.
| Задача 14.5. Оценить отношение сечений двух каналов
реакции фоторасщепления ядра О-16: а) б) |
Ядро 15N в основном состоянии имеет спин и четность JP = 1/2- и представляет собой - согласно модели оболочек - конфигурацию с одной "дыркой " относительно замкнутой подоболочки (ядра О-16 в основном состоянии) с квантовыми числами (n+1)lh jh = 1p1/2. Возбужденное состояние ядра 15N с JP = 3/2- - это "дырочное" состояние с (n+1)lh jh = 1p3/2, т.е. "дырка" в подоболочке 1p3/2. Число протонов на замкнутой подоболочке 1p1/2 равно 2, число протонов на замкнутой подоболочке 1p3/2 равно 4. Если энергия гамма-кванта значительно выше пороговых энергий обеих реакций ( как (а), так и (б)), то отношение сечений этих реакций будет определяться отношением вероятностей выбивания протона с подоболочек 1p1/2 и 1p3/2:
σа/σб![]() 1/2.
1/2.
Ядерные реакции с нейтронами
Как нейтроны, так и протоны участвуют в сильных
взаимодействиях с ядрами и нуклонами. Однако не обладающий электрическим зарядом
нейтрон не имеет кулоновского барьера в ядерных реакциях, поэтому ядерные
реакции под действием нейтронов играют особую роль в прикладной физике ядра.
Получение радиоактивных изотопов для медицинских и
технических целей производится путем облучения нейтронами стабильных изотопов.
Источником нейтронов является, например, ядерный реактор. Рассмотрим получение
радиоактивного изотопа на примере реакции активации золота
![]()
Полученный изотоп золота с А = 198 – радиоактивный. Он распадается с периодом полураспада Т1/2 = 2.7 суток
![]()
Рассмотрим изменение числа ядер золота 198 со временем, начиная от момента начала облучения золота 197:
dN(t) = Inσdt - λN(t)dt |
(14.2) |
Здесь I – поток нейтронов, n – число ядер золота 197 в образце, σ – эффективное сечение реакции активации.
| Задача 14.6. Определить активность препарата золота - 198, наведенную при облучении образца золота - 197 массой 0.1 г в потоке тепловых нейтронов 1012 см-2 сек-1 в течение 1 часа. Эффективное сечение активации золота тепловыми нейтронами составляет 97 барн. |
Активностью называется число распадов данного препарата в 1 сек. Активность равна вероятности распада на число ядер радиоактивного изотопа в образце
J(t) = λN(t) = Inσ(1-e-λt)
При условии, что время облучения t<<T1/2,
λt = t·ln2/T1/2<<1;
(1-e-λt)![]() 1 - 1 + λt
1 - 1 + λt
Учитывая, что n = m·Na/A, где m – масса активируемого образца, NA – число Авогадро,получаем, что наведенная активность изотопа золота - 198 составляет
![]()
Эффективные сечения реакций с нейтронами (как и других ядерных
реакций), зависят от кинетических энергий нейтронов. В случае, если захват
нейтронов приводит к экзотермической реакции - т.е. идет с выделением энергии, -
эффективное сечение захвата падает с ростом энергии в области Екин
<1 эВ (приблизительно по закону σ
Указанное в условиях задачи 14.6. значение эффективного
сечения активации золота соответствует энергии нейтронов, равной энергии
теплового движения. Такие энергии нейтронов достигаются путем замедления
нейтронов.
Замедление нейтронов
проводится с целью увеличения эффективных сечений реакций с нейтронами.
Для замедления нейтронов используется упругое рассеяние
нейтронов на ядрах вещества. Сечение реакций упругого
рассеяния
нейтронов на ядрах стремится к константе при уменьшении кинетической энергии
нейтрона.
При упругом рассеянии нейтронов на протонах в среднем за один
акт рассеяния нейтрон теряет половину своей энергии:
EN = EN-1cos2 |
(14.3) |
Здесь ЕN – кинетическая энергия нейтрона после N-го акта рассеяния на протоне.
(Докажите это соотношение, применив законы сохранения энергии и импульса к
реакции рассеяния нейтрона на протоне; учтите при этом, что mn![]() mp).
mp).
Таким образом, в качестве замедлителя может использоваться
любое водородосодержащее вещество – вода, парафин и т.д. Однако в ряде
приложений нейтронной физики, например, для поддержания цепной реакции деления,
важной характеристикой замедлителя является малое эффективное сечение захвата
нейтронов замедлителем. В этих случаях выбор замедлителя определяется как
эффективностью процесса уменьшения энергии нейтрона в замедлителе, так и низким
сечением захвата нейтронов. По этим характеристикам хорошими замедлителями
являются тяжелая вода (D2O) и графит. ( При использовании в качестве
замедлителя воды или других водородосодержащих веществ происходит значительный
захват нейтронов за счет реакции 1H(n,![]() )2H).
)2H).
При упругом рассеянии нейтронов на более тяжелых ядрах средние потери
кинетических энергий нейтрона меньше, чем при рассеянии на протонах. Например,
при рассеянии нейтронов на ядрах 12С ![]()
Снижение кинетических энергий нейтронов в процессах рассеяния
происходит вплоть до энергий теплового движения молекул в веществе
замедлителя. В этой области энергий распределение нейтронов по скоростям и
кинетическим энергиям близко к распределению Максвелла. Оценим среднюю
кинетическую энергию тепловых нейтронов при температуре замедлителя около 300о
К:
| Задача 14.7. Найти среднюю кинетическую энергию "теплового" нейтрона при температуре около 300К. Оценить среднее число актов упругого рассеяния нейтрона на протоне, необходимых для уменьшения кинетической энергии нейтрона от 4 МэВ до энергии теплового движения. |
Средняя кинетическая энергия теплового движения частицы с 3 степенями свободы равна Екин = (3/2)kT, где k - константа Больцмана. (k = 8.62.10-11 МэВ/K).
Eкин = 3kT/2![]() 0.04 эВ
0.04 эВ
Если в одном акте упругого рассеяния теряется около 1/2 кинетической энергии нейтрона, то среднее число актов рассеяния, необходимое для замедления, равно ~27, действительно
![]()
Цепная реакция деления
Реакция распада атомного ядра на два фрагмента сравнимой
массы называется делением. Деление бывает спонтанным и вынужденным (т.е.
вызванным взаимодействием с налетающей частицей). Реакция деления тяжелых ядер
под действием нейтронов лежит в основе методов получения ядерной энергии. По
кривой зависимости удельной энергии связи ядер от числа нуклонов А можно
оценить, какая энергия выделяется при превращении одного ядра с А ![]() 200 в два ядра с меньшими числа нуклонов.
Поскольку для тяжелых ядер энергия связи на нуклон около 7.5 МэВ, а для средних
– 8.5 МэВ, при делении этого ядра выделится энергия ~200 МэВ.
200 в два ядра с меньшими числа нуклонов.
Поскольку для тяжелых ядер энергия связи на нуклон около 7.5 МэВ, а для средних
– 8.5 МэВ, при делении этого ядра выделится энергия ~200 МэВ.
Основная часть энергии деления превращается в кинетическую
энергию “осколков” – т.е. получившихся в результате деления
ядер. Осколки, как правило, не имеют равных масс, в среднем
отношение из масс равно 1.46). Очень важной особенностью деления является то,
что для тяжелых ядер деление идет с испусканием нейтронов, как показывает пример
вынужденного деления урана-235:
n + 235U |
(14.4) |
 Рис.14.1. Эффективные сечения реакции деления изотопов урана под действием нейтронов |
Помимо реакции (14.4) вынужденное деление изотопа урана U-235
идет по десяткам других каналов деления. Важнейшей особенностью реакций
вынужденного деления ядер U-235 является тот факт, что для этого изотопа реакции
деления (n,f) не имеют энергетического порога, т.е. могут происходить на
тепловых нейтронах и поэтому имеют большие эффективные сечения. В среднем на
один акт деления изотопа 235U тепловыми нейтронам появляется 2.43
быстрых нейтрона. Именно те элементы, ядра которых при вынужденном делении дают
2-4 нейтрона в среднем на каждый акт деления, могут быть использованы для
поддержания цепной реакции деления. Цепная реакция деления будет поддерживаться
в том случае, если число нейтронов в одном поколении выше числа нейтронов в
предыдущем поколении. Реактор АЭС работает при коэффициенте размножения
нейтронов k > 1, поскольку часть родившихся нейтронов теряется за счет вылета за
пределы реактора и за счет других реакций (например, реакций захвата ![]() )).
)).
Практически используются для получения управляемой цепной
реакции деления всего три изотопа 235U, 238U, 239Pu,
причем третий изотоп – плутоний 239 – изготовляется в урановых ядерных
реакторах. Изотоп 238U испытывает деление только под действием
быстрых нейтронов с энергиями не ниже 1.1 МэВ.
Большинство промышленных ядерных реакторов (АЭС) работают на
обогащенном уране, т.е. смеси изотопов 238U и 235U, в
которой процентное содержание 235U значительно превышает долю этого
изотопа в естественной смеси (около 4.5 % вместо ~0.7%). Это так называемый "низкообогащенный"
уран. (Смесь изотопов урана с большим, чем 6%, содержанием 235U - "высокообогащенный"
уран - является материалом, используемым для изготовления ядерного оружия.)
Цепная реакция деления под действием тепловых нейтронов происходит на изотопе
235U. Этот изотоп урана под действием тепловых нейтронов делится на два
осколка – ядра с массовыми числами от 72 до 161 и числами протонов от 30 до 65.
Например, (14.4).
Полное эффективное сечение реакций деления 235U(n,f)
для тепловых нейтронов составляет около 580 барн.
Реакция деления изотопа 238U - пороговая, этот
изотоп делится только при энергиях нейтрона выше 1.1 МэВ, т.е. "быстрыми"
нейтронами. Однако эффективное сечение этой реакции деления значительно ниже,
чем сечение деления 235U(n,f) под действием тепловых нейтронов (см.
рис.14.1).
| Задача 14.8. Оценить энергию, выделившуюся в реакции вынужденного деления (14.4). Кинетические энергии нейтронов, вызывающих деление 235U, считать тепловыми. |
Энергия, выделившаяся в реакции, практически совпадает с разностью масс покоя ядер и нейтронов левой и правой частей (14.4), поскольку кинетической энергией тепловых нейтронов (~0.04 эВ) в балансе энергий можно пренебречь.
E = mn + M(235U) - M(95Sr) -
M(139Xe) - 2mn = Δ(235U)
- Δ(95Sr)
- Δ(139Xe)
- Δn =
= 40.92 + 75.05 + 75.69 - 8.07 = 182.59 МэВ.
Эта энергия распределяется между "осколками" деления и нейтронами,
испущенными в реакции деления.
Рождающиеся в процессе деления (например,14.4) нейтроны –
быстрые. Их необходимо замедлить до скоростей теплового движения,
чтобы использовать для деления других ядер 235U – то есть для
поддержания цепной реакции. С этой целью используются материалы, состоящие из
элементов с малым значением А. Чем меньше А, тем быстрее происходит замедление
нейтронов. (Замедление нейтронов происходит в реакции упругого рассеяния
нейтрона на ядрах замедлителя). Другим обязательным качеством замедлителя
является низкое значение эффективного сечения поглощения нейтронов. Таким
требованиям соответствует тяжелая вода, которая используется в гомогенных
реакторах. В гетерогенных реакторах в качестве замедлителя, как правило,
используется графит. В этом случае замедление нейтронов происходит на ядрах
углерода.
Одновременно с цепной реакцией деления 235U идет захват нейтронов изотопом 238U с последующим превращением его в плутоний:
n + 238U![]() 239U
+
239U
+ ![]() ;
;
239U![]() 239Np
+ e-
+
239Np
+ e-
+ ![]() e;
e;
239Np![]() 239Pu
+ e-
+
239Pu
+ e-
+ ![]() e.
e.
Образующийся в результате работы АЭС плутоний также
способен поддерживать цепную реакцию деления под действием медленных нейтронов.
Его используют как в АЭС, так и при производстве ядерного оружия.
В результате реакций деления появляются нестабильные ядра
("осколки" деления), “пересыщенные” нейтронами и испытывающие далее бета-распады
и гамма-переходы. Поэтому продукты деления имеют высокую радиоактивность.