Законы сохранения в распадах и реакциях
Структура и свойства частиц и атомных ядер исследуются уже
около ста лет в распадах и реакциях.
Распады представляют собой спонтанное превращение любого
объекта физики микромира (ядра или частицы) в несколько продуктов распада:
X → A + B + (C +...) |
(2.1) |
Реакция (в физике микромира) - это превращение двух взаимодействующих между собой объектов в два или более продуктов реакции:
X + Y → A + B + (С +...) |
(2.2) |
Как распады, так и реакции подчиняются ряду законов сохранения, среди которых должны быть упомянуты, во-первых, следующие законы:
1. Закон сохранения энергии: |
∑E = Сonst | (2.3) |
| 2. Закон сохранения импульса: | ∑P = Сonst | |
| 3. Закон сохранения момента количества движения | ∑ |
|
| 4. Закон сохранения электрического заряда | ∑Q = Сonst | |
| 4. Закон сохранения барионного заряда | ∑B = Сonst |
В дальнейшем будут обсуждаться и другие законы сохранения,
действующие в распадах и реакциях. Перечисленные выше законы являются важнейшими
и, что особенно существенно, выполняются во всех типах взаимодействий.
(Возможно, что закон сохранения барионного заряда не обладает такой
универсальностью, как законы сохранения 1-4, однако пока не обнаружено его
нарушения).
Процессы взаимодействий объектов микромира, отражением
которых являются распады и реакции, имеют вероятностные характерстики.
Распады
Спонтанный распад любого объекта физики микромира (ядра или частицы) возможен в том случае, если масса покоя продуктов распада меньше массы первичной частицы.
Распады характеризуются
вероятностями распада ![]() , либо обратной вероятности
, либо обратной вероятности ![]() величиной среднего времени жизни
τ = (1/λ). Часто
используется также связанная с этими характеристиками величина
периода полураспада
Т1/2.
величиной среднего времени жизни
τ = (1/λ). Часто
используется также связанная с этими характеристиками величина
периода полураспада
Т1/2.
Примеры спонтанных распадов
π0 → γ + γ; π+ → μ+ + νμ; |
(2.4) | n → p + e− +
μ+ → e+ + |
(2.5) |
В распадах (2.4) в конечном состоянии – две частицы. В распадах (2.5) – три.
Получим уравнение распада для частиц (или ядер). Убыль числа
частиц (или ядер) за интервал времени пропорциональна этому интервалу,
числу частиц (ядер) в данный момент времени и вероятности распада:
dN(t) = -λN(t)dt |
(2.6) |
Интегрирование (2.6) с учетом начальных условий дает для связи числа частиц в момент времени t с числом этих же частиц в начальный момент времени t = 0:
N(t) = N(0) exp(-λt) = N(0) exp(-t/τ) |
(2.7) |
| Задача 2.1. Получить соотношение между периодом полураспада, вероятностью распада и средним временем жизни. |
Периодом полураспада называется время, за которое число частиц (или ядер) уменьшится вдвое:
N(T1/2) = N(0)/2 = N(0) exp(-λT1/2) |
(2.8) |
Спонтанный распад любого объекта физики микромира (ядра или частицы) возможен в том случае, если масса продуктов распада меньше массы первичной частицы. Распады на два продукта и на три или более характеризуются разными энергетическими спектрами продуктов распада. В случае распада на две частицы спектры продуктов распада - дискретные. В случае, если частиц в конечном состоянии больше двух, спектры продуктов имеют непрерывный характер.
| Задача 2.2. Получить формулу для
кинетических энергий продуктов распада X |
Разность масс первичной частицы и продуктов распада
распределяется среди продуктов распада в виде их кинетических энергий.
Законы сохранения энергии и импульса для распада следует
записывать в системе координат, связанной с распадающейся частицей (или ядром).
Для упрощения формул удобно использовать систему единиц ![]() = c = 1,
= c = 1,
MX = MA + TA + MB + TB |
(2.9) |
Сумма кинетических энергий продуктов определяется разностью масс
TA/TB = MB/MA. |
(2.10) |
Отсюда получаем для кинетических энергий продуктов распада
TA = ΔM·MB/(MA + MB ); |
(2.11) |
Таким образом, в случае двух частиц в конечном состоянии
кинетические энергии продуктов определены однозначно.
Этот результат не зависит от того, релятивистские или нерелятивистские скорости
имеют продукты распада. Для релятивистского случая формулы для кинетических
энергий выглядят несколько сложнее, чем (2.10), но решение уравнений для энергии
и импульса двух частиц опять-таки является единственным. Это означает, что в
случае распада на две частицы спектры продуктов распада - дискретные.
Если в конечном состоянии возникает три (или более)
продуктов, решение уравнений для законов сохранения энергии и импульса не
приводит к однозначному результату. В случае, если частиц в конечном
состоянии больше двух, спектры продуктов имеют непрерывный характер. (В
дальнейшем на примере ![]() -распадов эта ситуация будет рассмотрена
детально.)
-распадов эта ситуация будет рассмотрена
детально.)
В расчетах кинетических энергий продуктов распада ядер удобно
воспользоваться тем фактом, что число нуклонов А сохраняется. (Это проявление
закона сохранения барионного заряда, поскольку барионные заряды всех
нуклонов равны 1).
Применим полученные формулы (2.11) к ![]() -распаду
226Ra (первый распад в (2.4)).
-распаду
226Ra (первый распад в (2.4)).
Разность масс радия и продуктов его распада
ΔM = M(226Ra) - M(222Rn) - M(4He) = Δ(226Ra) - Δ(222Rn) - Δ(4He) = (23.662 - 16.367 - 2.424) МэВ = 4.87
МэВ. (Здесь были использованы таблицы избытков масс нейтральных атомов и
соотношение ![]() для масс
и т.н. избытков масс Δ)
для масс
и т.н. избытков масс Δ)
Кинетические энергии ядер гелия и радона, возникших в
результате альфа-распада, равны:
![]() ,
,
![]() .
.
Суммарная кинетическая энергия, выделившаяся в результате альфа-распада, меньше 5 МэВ и составляет около 0.5% от массы покоя нуклона. Соотношение выделившейся в результате распада кинетической энергии и энергий покоя частиц или ядер - критерий допустимости применения нерелятивистского приближения. В случае альфа-распадов ядер малость кинетических энергий по сравнению с энергиями покоя позволяет ограничиться нерелятивистским приближением в формулах (2.9-2.11).
| Задача 2.3. Рассчитать энергии частиц, рождающихся в
распаде |
Распад π+
мезона происходит на две частицы: π+![]() μ++ νμ.
Масса π+
мезона равна 139.6 МэВ, масса мюона μ
равна 105.7 МэВ. Точное значение массы мюонного нейтрино νμ пока неизвестно, но установлено, что она не
превышает 0.15 МэВ. В приближенном расчете можно положить ее равной 0, поскольку
она на несколько порядков ниже разности масс пиона и мюона. Так как разность
масс π+ мезона и продуктов его распада равна 33.8
МэВ, для нейтрино необходимо использовать релятивистские формулы связи энергии и
импульса. В дальнейшем расчете малой массой нейтрино можно пренебречь и считать
нейтрино ультрарелятивистской частицей. Законы сохранения энергии и импульса в
распаде π+ мезона:
μ++ νμ.
Масса π+
мезона равна 139.6 МэВ, масса мюона μ
равна 105.7 МэВ. Точное значение массы мюонного нейтрино νμ пока неизвестно, но установлено, что она не
превышает 0.15 МэВ. В приближенном расчете можно положить ее равной 0, поскольку
она на несколько порядков ниже разности масс пиона и мюона. Так как разность
масс π+ мезона и продуктов его распада равна 33.8
МэВ, для нейтрино необходимо использовать релятивистские формулы связи энергии и
импульса. В дальнейшем расчете малой массой нейтрино можно пренебречь и считать
нейтрино ультрарелятивистской частицей. Законы сохранения энергии и импульса в
распаде π+ мезона:
mπ
= mμ + Tμ +
Eν
|pν| = |pμ|
![]()
Eν = pν
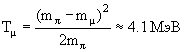
Примером двухчастичного распада является также излучение ![]() -кванта
при переходе возбужденного ядра на низший энергетический уровень.
-кванта
при переходе возбужденного ядра на низший энергетический уровень.
Во всех двухчастичных распадах, проанализированных выше,
продукты распада имеют «точное» значение энергии, т.е. дискретный спектр. Однако
более глубокое рассмотрение этой проблемы показывает, что спектр даже
продуктов двухчастичных распадов не является ![]() -функцией
энергии.
-функцией
энергии.
![]() .
.
Спектр продуктов распада имеет конечную ширину Г, которая тем больше, чем меньше время жизни распадающегося ядра или частицы.
Г·τ = ћ. |
(2.12) |
(Это соотношение является одной из формулировок соотношения неопределенностей
для энергии и времени).
Примерами трехчастичных распадов являются ![]() -распады.
-распады.
Нейтрон испытывает ![]() -распад, превращаясь в протон
и два лептона - электрон и антинейтрино:
-распад, превращаясь в протон
и два лептона - электрон и антинейтрино: ![]() p + e-
+
p + e-
+ ![]() e.
e.
Бета-распады испытывают и сами лептоны, например, мюон
(среднее время жизни мюона
τ
= 2.2 ·10–6 сек):
![]() .
.
|
(2.13) |
Особенности испускаемых нейтрино и антинейтрино будут обсуждаться на следующих семинарах, однако кинематику этого распада можно изучить и сейчас.
| Задача 2.4. Определить максимальную кинетическую энергию и импульс электрона в распаде мюона. |
Законы сохранения для распада мюона при максимальном
импульсе электрона:
Для максимальной кинетической энергии электрона распада мюона получим уравнение
![]()
Отсюда
|
(2.14) |
Кинетическая энергия электрона в этом случае на два порядка выше, чем его массы покоя (0.511 МэВ). Импульс релятивистского электрона практически совпадает с его кинетической энергией, действительно
p = (T2 + 2mT)1/2 = [532 + 2.0.511.53)1/2
МэВ![]() 53 МэВ.
53 МэВ.
(Отметим, что хотя расчеты кинематических характеристик принято проводить в
удобной системе единиц ![]() = с = 1,
= с = 1,
Рассмотрим распад частицы, происходящий исключительно
благодаря сильным (strong) взаимодействиям. Примером такого распада является
распад Δ-изобары Δ++ → p + π+.
| Задача 2.5. Оценить время жизни Δ-изобары по ширине распада Г ≈ 115 МэВ. |
Масса Δ-изобары равна 1232 МэВ , это самый легкий барион
из семейства Δ-изобар.
Разность масс первичной частицы и продуктов распада, т.е.
сумма кинетических энергий протона и пиона равна 154 МэВ. Из законов сохранения
энергии и импульса получаем
![]()
![]()
Для протона можно применить нерелятивистское приближение, однако для пиона оно не применимо. Решая уравнения для импульсов частиц, получаем для этого двухчастичного распада единственное, решение для кинетических энергий. Но спектр энергий пионов имеет ширину 115 МэВ и не является, строго говоря, дискретным. Столь большое значение ширины является следствием очень малого времени жизни Δ-изобары. Среднее время жизни этой частицы можно получить из соотношения (2.12):

Рассмотренные в этом разделе распады характеризовались, помимо спектров энергий продуктов, также и вероятностями распада (или обратными им средними временами жизни первичной частицы). Средние времена жизни частиц и ядер имеют колоссальный диапазон значений: например, среднее время жизни нестабильного бариона, называемого Δ-изобарой, меньше, чем 10–23 сек. Время жизни возбужденного ядра 12С ( в первом возбужденном состоянии) – порядка 10–13сек. Среднее время жизни мюона – около 2·10–6 сек, а среднее время жизни нейтрона около 12 минут. Поставим вопрос:
ЧТО ОПРЕДЕЛЯЕТ ВЕРОЯТНОСТЬ РАСПАДА НЕСТАБИЛЬНОЙ ЧАСТИЦЫ?
Вероятность распада является функцией
нескольких определяющих ее факторов.
Важнейшим из них является тип взаимодействия,
которое ответственно за происходящий распад. На первом семинаре была приведена
таблица свойств фундаментальных взаимодействий и указан порядок величин для
констант взаимодействия. Вероятности процессов, происходящих по тому или иному
типу взаимодействия, зависят (как правило) от квадрата константы взаимодействия.
Поэтому, поскольку распад Δ-изобары происходит по сильному взаимодействию, ему
соответствует высокая вероятность и малое время жизни (![]() 10-21
с). Процессы электромагнитного взаимодействия имеют константу примерно на два
порядка меньше сильных, соответствующие им средние времена жизни больше, чем
10-21
с). Процессы электромагнитного взаимодействия имеют константу примерно на два
порядка меньше сильных, соответствующие им средние времена жизни больше, чем ![]() 10-19
с. Слабые взаимодействия (примером которых являются
10-19
с. Слабые взаимодействия (примером которых являются ![]() -распады
(2.5)) имеют константу, примерно на 6 порядков меньшую, чем сильные
взаимодействия. Поэтому характерные для них средние времена жизни больше, чем 10-12
сек. Связь констант взаимодействия и вероятностей распадов определяет и наиболее
вероятный путь распада нестабильного ядра или частицы в случаях, когда возможны
несколько таких путей, т.н. каналов распада.
-распады
(2.5)) имеют константу, примерно на 6 порядков меньшую, чем сильные
взаимодействия. Поэтому характерные для них средние времена жизни больше, чем 10-12
сек. Связь констант взаимодействия и вероятностей распадов определяет и наиболее
вероятный путь распада нестабильного ядра или частицы в случаях, когда возможны
несколько таких путей, т.н. каналов распада.
Помимо типа взаимодействий, вероятность распада определяется
также 1) кинетической энергией излучаемых частиц и 2) моментами количества
движения, уносимыми излучением. Вероятность распада тем выше, чем больше
энергия перехода. Влияние этого фактора на вероятность распада часто
замаскировано влиянием второго фактора - т.е. уносимого излучением момента
количества движения. (Подробнее эта тема будет рассмотрена на семинаре 13).
Реакции
При расчете кинематических характеристик реакций удобно
использовать т.н. релятивистский инвариант ![]() = c = 1;
E - полная энергия системы, p - суммарный импульс.
= c = 1;
E - полная энергия системы, p - суммарный импульс.
В качестве примера использования инварианта рассмотрим
нахождение минимальной (т.е. пороговой)кинетической
энергии сталкивающихся частиц в эндотермической реакции
A + B |
(2.15) |
(В эндотермической реакции сумма масс покоя частиц ![]() mf,,
образующихся в конечном состоянии, больше суммы масс покоя первичных частиц
mf,,
образующихся в конечном состоянии, больше суммы масс покоя первичных частиц ![]() mi.) В системе покоя мишени (частицы
В) минимальная кинетическая энергия ТА, при которой возможна реакция
(2.15), называется порогом реакции. Для расчета порога реакции ТА
следует записать законы сохранения энергии и импульса в двух системах отсчета
– лабораторной системе, связанной с покоящейся частицей В, и в системе центра
масс, или центра инерции (штрихованные обозначения кинематических переменных):
mi.) В системе покоя мишени (частицы
В) минимальная кинетическая энергия ТА, при которой возможна реакция
(2.15), называется порогом реакции. Для расчета порога реакции ТА
следует записать законы сохранения энергии и импульса в двух системах отсчета
– лабораторной системе, связанной с покоящейся частицей В, и в системе центра
масс, или центра инерции (штрихованные обозначения кинематических переменных):
|
(2.16а) |
|
(2.16б) |
Порог реакции соответствует значению кинетической энергии частицы А в случае, когда кинетические энергии продуктов реакции минимальны. В системе центра масс в этом случае равны нулю кинетические энергии всех образовавшихся в результате реакции частиц. Одновременно равны нулю импульсы этих частиц. (Приравнять нулю импульсы и кинетические энергии продуктов реакции возможно только в системе центра инерции, в которой суммарный импульс по определению равен нулю). Найдем теперь значения E2 - p2 = inv для левой части уравнения (2.16а) (т.е. в лабораторной системе координат) и правой части уравнения (2.16б) (т.е. в системе центра масс) и приравняем их, используя таким образом свойство инвариантности:
|
(2.17) |
Из (2.17) получим
|
(2.18) |
где ![]() mi =
MA + MB.
mi =
MA + MB.
Иногда вместо формулы (2.18) используется эквивалентное ей
выражение
|
(2.19) |
где
Q = ![]() mi
-
mi
- ![]() mf
- энергия реакции
mf
- энергия реакции
| Задача 2.6. Рождение нейтрального π0 - мезона
на неподвижной водородной мишени происходит как на ускорителях электронов
промежуточных энергий, так и на ускорителях протонов. Сравнить минимальные
энергии пучков частиц на электронных и протонных ускорителях, при которых
возможно рождение π0 |
Реакции рождения π0-мезона на электронном и протонном ускорителях имеют следующий вид:
e + p |
(2.20) |
Пороговые энергии электронов и протонов в реакциях (4.26) будут соответственно
Te = mπ(2mp + 2me + mπ)/2mp
Tp = mπ(4mp + mπ)/2mp
Пользуясь таблицами масс, получим для пороговых кинетических энергий электрона и протона в реакциях (2.20):
Te = 135 МэВ (2·938 МэВ + 1 МэВ + 135 МэВ) / (2·938 МэВ)![]() 145
МэВ,
145
МэВ,
Tp = 135 МэВ (4·938 МэВ + 135 МэВ) / (2·938 МэВ)![]() 280
МэВ.
280
МэВ.
Столь значительное различие в пороговых энергиях при
рождении пиона в реакциях электронов и протонов с неподвижной водородной мишенью
является следствием больших затрат энергии на движение центра масс системы во
второй реакции. Эти затраты отсутствуют в ускорителях на встречных пучках –
коллайдерах (colliders). Именно коллайдеры являются основным инструментом
современной физики высоких энергий в получении информации о структуре и
свойствах частиц и их взаимодействий.
Определим энергию ![]() частицы в ускорителе с
неподвижной мишенью, эквивалентном коллайдеру с энергиями E одинаковых частиц в
пучках.
частицы в ускорителе с
неподвижной мишенью, эквивалентном коллайдеру с энергиями E одинаковых частиц в
пучках.
В ускорителе со встречными пучками одинаковых по массе частиц
лабораторная система совпадает с системой центра масс. В этой системе E2 - p2 = inv = 4E2.
В системе координат, связанной с одной из сталкивающихся частиц (например,
частицей 2) энергия частицы 1 есть искомая энергия ![]() . В этой системе квадрат
полной энергии равен (m + m +
. В этой системе квадрат
полной энергии равен (m + m + ![]() )2,
а квадрат полного импульса системы равен квадрату импульса частицы 1: p2 = (p1)2 =
)2,
а квадрат полного импульса системы равен квадрату импульса частицы 1: p2 = (p1)2 = ![]() 2 - m2.
Приравнивая значения инвариантов в этих двух системах, получим для энергии
частицы в ускорителе с неподвижной мишенью, эквивалентном коллайдеру
2 - m2.
Приравнивая значения инвариантов в этих двух системах, получим для энергии
частицы в ускорителе с неподвижной мишенью, эквивалентном коллайдеру
|
(2.21) |
| Задача 2.7. Оценить, какие энергии пучков должны
иметь ускорители с неподвижной мишенью, эквивалентные
ускорителям на встречных пучках: а) протон-антипротонному коллайдеру (лаборатория им.Ферми FNAL) с энергиями пучков 1ТэВ; б) электрон –позитронному коллайдеру (LEP,CERN) с энергиями пучков 100 ГэВ. (Теватрон завершил свою работу в 2011 году после 28 лет эксплуатации. В 2000 году эксперименты на LEP были завершены и ускоритель был демонтирован. В настоящее время в этом же туннеле размещен новый ускоритель — большой адронный коллайдер.) |
Расчет энергий пучков в ускорителях с неподвижной мишенью, эквивалентных коллайдеру по (4.27), дает соответственно для энергий антипротонов
![]()
и для энергий позитронов
![]()
Относительно больший «выигрыш» в энергии для коллайдеров с электронными и позитронными пучками является следствием зависимости энергии «эквивалентного» ускорителя с неподвижной мишенью (см. (4.27)) от массы ускоряемых частиц.
| Задача 2.8. Определить минимальную кинетическую энергию протона в реакции рождения «странных» частиц p + p → p + K+ + Σ0 в условиях ускорителя с неподвижной водородной мишенью и в условиях протон-протонного коллайдера. |
В ускорителе с неподвижной мишенью
![]()
В условиях коллайдера кинетические энергии обоих протонов идут - в предельном случае - на создание масс продуктов. Поэтому минимальная (пороговая) энергия протона в коллайдере равна половине разности масс продуктов реакции и первичных частиц, что в данном случае составляет всего около 375 МэВ.
