©hoo$e ЛÄнgიAge©///₾ÄngიAge® Ekohomei©Å TÅLKiNg ი.ბ.м.ლ.

geo.rf.gd

   

Распады нестабильных ядер

    Основные характеристики распадов частиц и ядер обсуждались на первых семинарах. Была выведена формула связи периода полураспада Т1/2, вероятности распада λ и среднего времени жизни tau для частицы или ядра, испытывающих спонтанный распад:

T1/2 = ln2/λ=  τln2.

(13.1)

    Там же было показано, что распады на два продукта и на три или более характеризуются разными энергетическими спектрами продуктов распада. В случае распада на две частицы спектры продуктов распада − дискретные. Примером таких распадов являются все альфа-распады ядер. (Напомним, что законы сохранения энергии и импульса для распадов следует записывать в системе координат, связанной с распадающейся частицей или ядром. Для упрощения формул удобно использовать систему единиц ћ = c = 1, в которой энергия, масса и импульс имеют одну и ту же размерность).
    Если продукты распада X → A + B - нерелятивистские, кинетические энергии продуктов распада связан очень простым образом с разностью масс покоя частицы X и продуктов распада А и В

TA =  ΔM·MB/(MA  + MB ); TB =  ΔM·MA/(MA  + MB ). (формулы 2.11).

На семинаре 2 были получены кинетические энергии ядер радона и гелия, возникающих в результате альфа-распада ядра радия:

,
.

    Полученные значения кинетических энергий ядер радона и гелия оправдывают применение нерелятивистского приближения. Для оценки справедливости этого приближения нет необходимости рассчитывать скорости продуктов и сравнивать их со скоростью света, достаточно сравнить кинетическую энергию частицы с ее энергией покоя. В распаде радия-226 максимальную кинетическую энергию уносит ядро гелия (т.е. альфа-частица), причем эта энергия составляет меньше 0.5% энергии покоя нуклона (~940 МэВ) и, соответственно, меньше, чем 0.15% энергии покоя ядра гелия.
    Возникающее в результате альфа-распада радия (Т1/2 =1600 лет) ядро радона также испытывает альфа-распад с периодом полураспада Т1/2 = 3.82 дня.

Задача 13.1. Рассчитать кинетическую энергию альфа-частицы в распаде 222Rn → 218Po + 4He.

ΔM = Δ(222Rn) - Δ(218Po) - Δ(4He) = 5.59 МэВ; T(4He) = 218.5.59/222 = 5.46 МэВ.
   Возникающий в этом распаде полоний-218 также распадается с излучением альфа-частиц (период его полураспада Т1/2 = 3.1 мин): 218Po → 214Pb + 4He. Продукт этого распад 214Pb "перегружен" нейтронами (стабильными являются изотопы свинца 206Pb, 207Pb, 208Pb). Поэтому 214Pb распадается (Т1/2 = 27 минут) по каналу бета-распада.
    Рассмотренная нами "цепочка" распадов является характерной особенностью распадов тяжелых ядер. Образовавшиеся при синтезе элементов более 10 миллиардов лет тому назад тяжелые ядра распадаются, образуя снова нестабильные ядра. Распады продолжаются вплоть до образования стабильных элементов. В распадах происходит излучение альфа-частиц и пар лептонов (бета-распады). В альфа-распадах число нуклонов А в ядрах изменяется на 4 , бета-распады происходят без изменения А. Поэтому существует всего 4 ряда (семейства) радиоактивных распадов тяжелых ядер с массовыми числами А = 4n, 4n + 1,4n + 2 и 4n + 3.

Таблица 13.1

А Исходное ядро T1/2 Конечное ядро
4n Th-232 1.4·1010л Pb-208
4n+1 Np-237; U-233 2.1·106л; 1.6·105л Bi-209
4n+2 U-238 4.5·109л Pb-206
4n+3 U-235 7.0·108л Pb-207

Первичные ядра второго из семейств с А = 4n + 1 практически распались за время, прошедшее после их образования. Распады остальных трех рядов являются источником радиоактивности вещества Земли. Рассмотренные выше распады 226Ra, 222Rn, 218Po относятся к семейству 4n + 2.

Задача 13.2. Оценить отношение активностей отдельных членов радиоактивного семейства 4n+2.

    Период полураспада 238U на несколько порядков величины больше, чем периоды полураспадов всех остальных членов радиоактивного семейства. Для всех членов семейства, например i-го, (за исключением первого - 238U и последнего - стабильного изотопа 206Pb) , изменение числа ядер связано с ростом числа ядер за счет распада предыдущего члена "цепочки", т.е. (i-1) элемента, и распадом ядер данного i-го элемента:

dNi/dt = λi-1Ni-1 - λiNi.

За время, прошедшее после образования элементов, установилось т.н. "вековое" равновесие, когда прибыль и убыль ядер данного нестабильного элемента в цепи распадов компенсируют друг друга. При этом активности (т.е. числа распадов в 1 секунду) всех членов радиоактивного семейства выравниваются:

λi-1Ni-1 = λiNi = λi+1Ni+1 = ...

    Активность радиоактивного препарата, т.е. число распадов в секунду, которое этот препарат испытывает, определяется не только числом распадов в единицу времени первичного ядра, но и активностями всех получаемых в результате распадов продуктов. Часто эти продукты распадов вносят в суммарную активность значительно больший вклад, чем первичный распад.
    Распад с излучением ядер гелия - альфа-распад - возможен потому, что внутри ядер возможно образование кластеров - систем из нескольких нуклонов. Наибольшей вероятностью обладает как раз образование альфа-кластеров, или ядер гелия, поскольку ядра гелия имеют большую энергия связи на нуклон и , соответственно, меньшую массу, чем сумма масс 2 протонов и 2 нейтронов. Туннельный эффект делает возможным испускание таких альфа-кластеров, если сумма масс продуктов реакции меньше массы исходного ядра. Но в распадах нестабильных ядер возможно рождение частиц, которые отсутствовали в начальном состоянии системы. Таким процессом является бета-распад.
    Примером бета-распада является распад нейтрона n → p + e- + антинейтриноe. Среднее время жизни нейтрона
τ = (886.7 + 1.9) с.
    Масса нейтрона больше суммы масс протона и электрона, что и определяет возможность его спонтанного распада. Массы электронного нейтрино и антинейтрино меньше 2 эВ и в дальнейших расчетах бета-распадов их можно считать равными 0.
    Следует отметить, что проблема строгого равенства (или неравенства) нулю нейтринных масс представляет собой важнейшую задачу современной физики. Данные последних экспериментов свидетельствуют в пользу неравенства нулю масс нейтрино.
    В ядрах как нейтроны, так и протоны находятся в связанном состоянии. Спонтанные превращения связанных в ядре нуклонов друг в друга возможны и определяются соотношением масс начального ядра и продуктов распада.
   Бета-распад ядер может происходить с вылетом электронов (β--распад), с вылетом позитронов
(β+-распад) и путем захвата электрона с оболочек атома (е-захват). Ниже приведены примеры этих процессов:

14C → 14N + e- + антинейтриноe;
11C → 11B + e+ + νe;
7Be → 7Li + νe.

(13.2)

    Рассмотрим закон сохранения энергии для этих процессов. Напомним, что в таблицах для масс (или избытков масс) приведены массы нейтральных атомов, к которым и следует привести уравнения для законов сохранения. В дальнейших выкладках массы нейтральных атомов не помечены индексами, а для масс ядер введен индекс N (nucleus).
    Для β--распада:

MN(Z,A) = MN(Z+1,A) + me + TN + Te + Eν;
M(Z,A) neqv MN(Z,A) + Zme;
M(Z,A) = M(Z+1,A) + TN + Te + Eν.

(13.3)

    Для β+-распада получим аналогичным образом из уравнения для масс ядер уравнение для масс нейтральных атомов:

M(Z,A) = M(Z-1,A) + 2me + TN + Te + Eν.

(13.4)

    Для е-захвата:

M(Z,A) = M(Z-1,A) + TN + Eν.

(13.5)

Сравнение двух последних уравнений показывает, что для двух ядер-изобар е-захват имеет менее “жесткие” энергетические условия, чем β+-распад. (В обоих случаях происходит превращение одного из протонов ядра в нейтрон). Однако поскольку е-захват представляет собой захват ядром электрона с атомной оболочки, вероятность этого процесса пропорциональная вероятности W “пребывания электрона внутри ядра”, т.е.

.

(13.6)

Вероятность захвата К-электрона во много раз выше, чем электронов с других атомных оболочек, т.к. для К-электронов величина интеграла в (13.6) больше, чем для электронов других оболочек.
    Законы сохранения энергии для β- и β+- распадов имеет важную общую особенность. В обоих случаях число уравнений (закон сохранения энергии + закон сохранения импульса) на единицу меньше числа неизвестных – кинетических энергий продуктов реакций. Следствием этого факта является непрерывный спектр продуктов этих процессов распада. Именно непрерывный характер спектра электронов бета--распада послужил доказательством существования нейтрино задолго до его непосредственного экспериментального обнаружения. Спектры продуктов трехчастичных распадов имеют т.н “верхнюю границу”- максимальное значение кинетической энергии. Оно соответствует той кинематической ситуации, когда данная частица имеет направление импульса, противоположное импульсам обеих других частиц.
   Суммарный спин S, уносимый лептонами при бета-распаде, может быть либо 0, либо 1. Переходы первого типа (S = 0) называются фермиевскими, второго типа (S = 1) - гамов-теллеровскими. Многие бета-распады (например, распад нейтрона) являются смесью переходов первого и второго типов.

Задача 13.3. Рассчитать верхнюю границу спектра электронов распада ядра трития
3H → 3He + e- + антинейтриноe.

TN + Te + Eν = M(3H) - M(3He) = Δ(3H) - Δ(3He) = 14.950 - 14.931 = 0.019 МэВ.
Закон сохранения импульса этого процесса

.

Электрон имеет максимальный импульс и максимальную энергию, если

pe = pN + pν = [2M(3He)TN]1/2 + Eν.

Здесь использован тот факт, что для кинетической энергии ядра применимо нерелятивистское приближение, а нейтрино (точнее - антинейтрино) – ультрарелятивистская частица. Импульс конечного ядра не превышает суммы модулей импульсов лептонов (электрона и антинейтрино). Поскольку масса ядра более чем на три порядка величины превышает массу электрона, кинетическая энергия ядра примерно на три порядка меньше суммы кинетических энергий лептонов.
    Сумма кинетической энергии электрона и энергии антинейтрино поэтому приближенно равна разности масс начального и конечного атомов, т.е.

Te + Eν = 0.019 МэВ = 19 кэВ.
(Te)max = 19 кэВ.

Электрон уносит максимальную кинетическую энергию, если энергия антинейтрино, излучаемого вместе с ним, близка к 0. Максимальная энергия, которую может унести антинейтрино этого распада, равна максимальной энергии электрона. Антинейтрино уносит максимальную энергию в случае, когда кинетическая энергия электрона близка к 0.

Задача 13.4. Оценить кинетическую энергию протона в β--распаде нейтрона. 

    Разность масс покоя начального и конечного состояний в распаде n → p + e- + антинейтриноe равна 0.782 МэВ. В случае, когда электрон уносит максимальную энергию

Teneqv 0.782 МэВ, Eν ≈ 0.

Импульс электрона в этом случае равен и противоположен по направлению импульсу протона. Кинетическая энергия нерелятивистского протона

В случае, когда максимальную энергию уносит антинейтрино, кинетическая энергия протона

В рассмотренных примерах бета-распадов разность масс покоя начального и конечного состояний практически полностью уносилась двумя лептонами. Это является следствием большой, сравнительно с лептонами, массы конечного ядра (в последнем примере - протона).

Задача 13.5. Определить энергию нейтрино, излучаемого при е-захвате К-электрона ядром 7Ве:
7Be + e- → 7Li + νe.

Сумма энергии нейтрино и энергии отдачи ядра лития равны

Eν + TLi = Δ(7Be) - Δ(7Li) = 15.768 - 14.907 = 0.861 МэВ.

(Энергией связи электрона на атомной орбите в данном расчете можно пренебречь).

Импульсы нейтрино и ядра лития равны и противоположны, поэтому

Действуя методом последовательных приближений, получим

Eν ≈ 0.86 МэВ;

Таким образом, спектры энергий продуктов е-захвата имеют дискретный характер.

Задача 13.6. Определить энергию гамма-кванта и кинетическую энергию отдачи ядра при излучении гамма-кванта возбужденным ядром (12С)*, находящимся в первом возбужденном состоянии с квантовыми числами 2+, Е = 4.43 МэВ. 12С* → 12С + γ.

Законы сохранения в системе покоя возбужденного ядра имеют вид:

M(12C*) = M(12C) + TC + Eγ; pC = pγ = Eγ;
E(12C*) = M(12C*) - M(12C) = 4.43 МэВ = TC + Eγ;

Поскольку второй член (энергия отдачи) в последнем уравнении на несколько порядков меньше первого, вместо решения квадратного уравнения удобно применить метод последовательных приближений:

(В данном случае нет смысла уточнять первое приближение для энергии гамма-кванта – поправка равна энергии отдачи ядра и она меньше последней значащей цифры в полученном результате для энергии испущенного ядром электромагнитного кванта.)
    Во всех двухчастичных распадах, проанализированных выше, продукты распада имеют “точное” значение энергии, т.е. дискретный спектр. Однако более глубокое рассмотрение этой проблемы показывает, что спектр даже продуктов двухчастичных распадов не является δ-функцией энергии. Спектр продуктов распада имеет конечную ширину Г, которая тем больше, чем меньше время жизни распадающегося ядра или частицы.

Г·τ = ћ.

(13.7)

(Это соотношение является одной из формулировок соотношения неопределенностей для энергии и времени)

Вероятности распадов

    Рассмотренные в предыдущих семинарах распады частиц и ядер характеризовались, помимо спектров энергий продуктов, также и вероятностями распада (или обратными им средними временами жизни первичной частицы). Средние времена жизни имеют колоссальный диапазон значений: например, среднее время жизни нестабильного бариона, называемого Δ-изобарой, меньше, чем 10–23 сек. Время жизни возбужденного ядра 12С – порядка 10–13сек. Среднее время жизни мюона – около 2·10–6 сек, а среднее время жизни нейтрона около 12 минут. На семинаре 2 уже обсуждался вопрос о факторах, определяющих вероятность распада нестабильной частицы или ядра. Напомним, что вероятность распада частицы или ядра является функцией нескольких определяющих факторов.
    Важнейшим из них является тип взаимодействия, которое ответственно за происходящий распад. Вероятности процессов, происходящих по тому или иному типу взаимодействия, зависят (как правило) от квадрата константы взаимодействия (См. семинар 3). Например, поскольку распад дельта-изобары происходит по сильному взаимодействию, ему соответствует высокая вероятность и малое время жизни, около 10–23сек. Процессы электромагнитного взаимодействия имеют константу примерно на два порядка меньше сильных, соответствующие им средние времена жизни больше, чем 10-19 сек. Слабые взаимодействия ( примером которых являются рассмотренные выше бета-распады ядер и нуклонов) имеют константу, примерно на 6 порядков меньшую, чем сильные взаимодействия. Поэтому характерные для них средние времена жизни больше, чем 10-12 сек. Связь констант взаимодействия и вероятностей распадов определяет и наиболее вероятный путь распада нестабильного ядра или частицы в случаях, когда возможны несколько таких путей, т.н. каналов распада.

Задача 13.7. Определить наиболее вероятные каналы распада ядра 12С, находящегося в возбужденном состоянии с энергией возбуждения 22 МэВ.

    Поскольку энергия возбуждения ядра выше энергий отделения протона (15.96 МэВ) и энергии отделения нейтрона (18.72 МэВ) от этого ядра, оно будет распадаться по каналу сильного взаимодействия с вылетом нуклонов:

12С* → 11B + p, либо  12С*----->11С + n.

    Помимо типа взаимодействий, вероятность распада определяется также 1) кинетической энергией излучаемых частиц и 2) моментом количества движения, уносимым излучением.
   Вероятность распада тем выше, чем больше энергия перехода. Влияние этого фактора на вероятность распада часто замаскировано влиянием второго фактора - т.е. уносимого излучением момента количества движения.

Рассмотрим влияние этих факторов на примере бета-распада ядра 60Со (Рис.13.1)


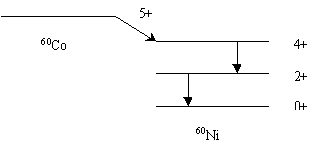Рис.13.1

    Возбужденные состояния ядра 60Ni представляют собой типичный спектр коллективных колебаний. Энергетический интервал между первым и основным состояниями близок к интервалу между первым и вторым состояниями. Ядро 60Со может превращаться в ядро - изобар 60Ni путем бета-распада по нескольким энергетически возможным каналам:
1) в основное состояние конечного ядра,
2) в первое возбужденное состояние со спином 2+,
3) во второе возбужденное состояние 4+.
    Энергетически наиболее выгоден первый канал, для которого сумма кинетических энергий, выделяющаяся в бета-распаде, максимальна. Однако в действительности практически 100% бета-переходов происходит по наименее энергетически выгодному пути - бета-распад ядра 60Со идет на второй возбужденный уровень 60Ni со спином 4+. Для понимания причины того, почему именно этот канал распада оказывается наиболее вероятным, рассмотрим закон сохранения момента количества движения для бета-распада ядра 60Со: 60Со → 60Ni + e- + антинейтриноe

vec_Ji = vec_Jf + vec_se + vec_sν + vec_le+ν.

(13.8)

Здесь vec_le+ν сумма орбитальных моментов, уносимых лептонами бета-распада. Распишем закон сохранения момента (4.19) для трех каналов beta-распада 60Со и найдем возможные значения vec_le+ν для каждого канала:

= vec_0 + vec_1/2 + vec_1/2 + vec_le+ν,   le+ν = 4, 5, 6
= vec_2 + vec_1/2 + vec_1/2 + vec_le+ν,   le+ν = 2, 3, 4, 5, 6, 7, 8
= + vec_1/2 + vec_1/2 + vec_le+ν,   le+ν = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Применение закона сохранения момента количества движения к трем возможным каналам распада кобальта показывает, что только при бета-распаде на возбужденный уровень со спином 4 орбитальный момент, уносимый электроном и нейтрино, может быть равен нулю. Это т.н. “разрешенный” переход. Он и осуществляется почти со 100% вероятностью, хотя энергетически из всех открытых каналов распада он наименее выгоден. Хотя прямое доказательство того факта, что бета-распад с нулевым значением орбитального момента лептонов имеет наибольшую вероятность, осуществляется лишь методами квантовой теории поля, помочь в понимании этого явления может “классическая” оценка максимального значения орбитального момента лептонов распада. Одновременно эта оценка служит интересной иллюстрацией соотношения классической и квантовой теорий. С классической точки зрения, максимальное значение орбитального момента лептонов распада равно L = Rpmax, где R - радиус ядра (например с А = 60) , а pmax - максимальное значение импульса суммы лептонов. В пределе, когда максимальная кинетическая энергия распада T уносится антинейтрино, T = pmaxc.  Тогда максимальный орбитальный момент (в единицах ћ) оказывается равным

l = Rpc/ћc = RT/ћc ≤ 1/10 <<1

(13.9)
 

Рис.13.2

    Таким образом, в “классическом” пределе вылет лептонов с ненулевым орбитальным моментом вообще невозможен, “запрещен”. Квантовый, т.е. реальный, мир имеет гораздо больше возможностей, но в нем с наибольшей вероятностью происходят именно те события, которые “разрешены” классической физикой.
β-распад, в которых орбитальный момент, уносимый лептонами, равен 0, называется в физике ядра разрешенным. Орбитальному моменту 1 соответствует запрещенный переход первого порядка, орбитальному моменту 2 - запрещенный переход второго порядка и т.д. Если другие каналы распада энергетически невозможны -“закрыты”- осуществляется “запрещенный” β-распад, но вероятность его будет мала, а среднее время жизни и период полураспада - велики. Примером такого бета-перехода является распад ядра 40К (см. рис. 13.2). Спин и четность основного состояния этого ядра равны 4-. Ядро 40К может испытывать е-захват (с вероятностью 10.7%), превращаясь в 40Ar, либо β--распад в основное состояние ядра 40Са (89.3%). Оба канала соответствуют “запрещенным” β-переходам с запретами первого и третьего порядков. В итоге β-распад 40К происходит с периодом полураспада 1.28·109 лет. Сравнение количества аргона-40 и калия-40 в минералах является методом определения возраста горных пород.

Задача 13.8. Оценить верхнюю границу возраста Земли Т, считая, что весь присутствующий на Земле аргон-40 возник в результате е-захвата из 40К. В настоящее время на 1 ядро 40К приходится примерно 300 ядер аргона-40.

Число ядер аргона равно числу распавшихся за время Т ядер К-40, умноженному на вероятность распада:



T neqv1.5.1010 лет.

Электромагнитное излучение атомных ядер

    Вероятности излучения гамма-квантов возбужденными ядрами зависят от энергии E излучаемого кванта и от его мультипольности J – т.е. полного момента количества движения. По соотношению четности и мультипольности различают два типа гамма-излучения:

Электрическое (EJ), для которого четность P = (-1)J ;
Магнитное (MJ), для которого четность P = (-1)J+1.

(13.10)

    Точные выражения для вероятностей излучения гамма-кванта ядром весьма сложны, в них, помимо энергии (или длины волны излучаемого кванта) и мультипольности излучения входят также квадраты матричных элементов операторов перехода между начальным и конечным состояниями ядра. Для приближенных оценок соотношений вероятностей гамма-переходов можно использовать следующую зависимость вероятностей от мультипольности и длины волны излучаемого гамма-кванта:

.

(13.11)

Отношение радиуса ядра-излучателя и приведенной длины волны излучаемого гамма-кванта много меньше единицы. Поэтому из (13.11) следует, что чем ниже мультипольность излучения, тем вероятнее гамма-переход. Минимальная мультипольность гамма-кванта равна 1 – т.е. спину гамма-кванта

Задача 13.9. Для гамма-переходов ядра 60Ni с энергиями около 1 МэВ оценить отношение радиуса ядра к приведенной длине волны.

lambda/ = ћс/Eγ = 200 Фм; R(60Ni) ≈ r0A1/3 = 5 Фм; R/lambda/ ≈ 0.025.

Задача 13.10. Для ядра 60Ni во втором возбужденном состоянии, возникшем в результате гамма-распада 60Со (см. схему распада кобальта-60), определить наиболее вероятный путь гамма-переходов в основное состояние. Указать мультипольность и тип излучаемых гамма-квантов.

    Рассмотрим законы сохранения момента импульса для двух возможных каналов гамма-переходов из второго возбужденного состояния ядра 60Ni со спином 4+:

4+----->2+: = vec_2 + vec_J; J = 2, 3, 4, 5, 6.
4+----->0+: = 0 + vec_J; J = 4.

Для первого из переходов возможная мультипольность излучения меньше, чем для второго. Наиболее вероятным будет излучение гамма-кванта с мультипольностью 2. Поскольку четности начального и конечного состояния ядра 60Ni одинаковы , четность излучения положительна. Следовательно, из состояния 4+ будет излучаться Е2 гамма-квант. Ядро 60Ni перейдет в первое возбужденное состояние со спином 2+. Переход в основное состояние также будет осуществляться путем излучения Е2 гамма-кванта, Энергии этих двух “каскадных” квантов равны 1.17 и 1.33 МэВ.

Задача 13.11. Для гамма-переходов из второго возбужденного уровня ядра 60Ni оценить отношение вероятностей переходов W(4+----->2+)/W(4+----->0+).

    Учитывая, что lambda/ = h/с/Eγ; R ≈ r0A1/3   получим для отношения вероятностей по формуле(13.11):

Результат этой задачи объясняет, почему в большинстве случаев высоковозбужденные состояния атомных ядер переходят в основное состояние путем последовательного высвечивания нескольких гамма-квантов. Например, вращательные полосы четно-четных ядер были исследованы путем измерения энергий каскада Е2 (электрических квадрупольных) гамма-квантов.

Задача 13.12.Определить тип и мультипольность гамма-излучения из первого возбужденного состояния ядра 137Ва.

Рис.13.3

    Радиоактивный изотоп 137Cs с периодом полураспада 30 лет превращается путем бета-распада в ядро 137Ва, причем 92% бета-переходов происходит на первый возбужденный уровень ядра-продукта со спином и четностью JP = (11/2)- (см.рис.13.3). Спин и четность основного состояния ядра 137Ва равны (3/2)+.Минимальная мультипольность излучаемого с первого возбужденного уровня гамма-кванта равна 4, четность (–1):

  J = 4, 5, 6. 7.
P = (-1).(+1).

Получаем, что с первого возбужденного уровня 137Ва должен излучаться либо гамма-квант М4, либо Е5. Вероятности излучений этих двух квантов, согласно приближенной формуле (13.8), близки. Поскольку мультипольности обоих квантов велики, вероятности их излучения малы по сравнению с вероятностями излучений квантов меньшей мультипольности; времена жизни ядер в таких возбужденных состояниях относительно велики. Такие состояния называются метастабильными, а переходы с этих состояний – изомерными переходами.
    В рассмотренных выше примерах электромагнитного излучения возбужденных ядер использовалось сохранение пространственной четности Р. В отличие от слабого взаимодействия, проявляющегося в гамма-распадах ядер, в электромагнитных и сильных взаимодействиях четность сохраняется.
    Совместное применение законов сохранения момента импульса и пространственной четности является методом анализа возможности распадов и реакций, происходящих по сильному или электромагнитному взаимодействию.
    В распадах по каналам сильных взаимодействий проявляется также закон сохранения изоспина. Рассмотрим нуклонные распады высоковозбужденных состояний ядер с изоспином Inoneqv0 в основном состоянии. В ядерных реакциях, например, при неупругом рассеянии электронов, изоспин ядра может измениться на 1. Проекция изоспина при этом остается прежней, т.к. она определена числом протонов и нейтронов в ядре.

Задача 13.13.Применив закон сохранения изоспина к нуклонным каналам распада возбужденных состояний ядра 11В, доказать невозможность распада состояний с изоспином 3/2 по нейтронному каналу. (Энергия возбуждения ядра 11В выше энергий отделения нейтрона либо протона).

    Закон сохранения энергии будет выполнен при распаде возбужденных состояний ядра В-11 как по протонному, так и по нейтронному каналам распада, если энергия возбуждения ядра выше энергий отделения нуклонов. Эти распады происходят по сильным взаимодействиям, в которых должен быть выполнен закон сохранения изоспина системы. Изоспин ядра 11В в основном состоянии равен 1/2, проекция изоспина I3 = –1/2. Возбужденные состояния 11В, при той же проекции, могут иметь изоспин 1/2 и 3/2. (Такие возбужденные состояния возникают, например, при поглощении гамма-квантов высокой энергии, поскольку изоспин гамма-кванта может быть как 0, так и 1)
    Закон сохранения изоспина в распадах по протонному каналу выполняется для обоих изоспиновых состояний, но не выполняется для нейтронного распада из состояний с изоспином 3/2:

11В → 10Вe + p;   I(10Вe) = 1;
vec_1/2 = vec_1 + vec_1/2;  vec3_2 = vec_1 + vec_1/2.		 11В → 10В + n;   I(10В) = 0;
vec_1/2 = 0 + vec_1/2;  vec3_2 ≠ 0 + vec_1/2.

Таким образом, нейтронный распад из возбужденных состояний ядра 11В с изоспином 3/2 запрещен правилами отбора по изоспину.

Задание 5

  1. Рассчитать верхнюю границу спектра электронов распада трития: 3H → 3He + e- + антинейтриноe. Определить вероятное значение орбитального момента пары лептонов.
  2. По массам изобар с А = 13 найти верхнюю границу спектра позитронов распада ядра 13N. Определить, относится этот распад к разрешенным или запрещенным бета-переходам.
  3. По массам ядер-изобар 14С и 14N определить верхнюю границу спектра бета-распада и установить, относится переход к фермиевскому или гамов-теллеровскому типу распада.
  4. Оценить кинетическую энергию ядра 7Li, образующегося при Е-захвате электрона ядром 7Be.
  5. Найти кинетические энергии альфа-частиц, возникающих при распаде ядра 8Be.
  6. Рассчитать количество тепла, выделившееся при распаде 1 кг плутония (239Pu) в течение месяца. Период полураспада плутония 24000 лет.
  7. Определить тип (электрический, магнитный) и мультипольность гамма-квантов, возникающих при переходах ядра 13С из первого возбужденного состояния 1/2+ (E = 3.09 МэВ) в основное состояние.
  8. Объяснить, почему бета--распад ядра 24 Na (спин и четность основного состояния 4+) происходит не на основной (0+) или первый возбужденный (2+), а на второй возбужденный (4+) уровень ядра 24 Mg.
  9. Указать наиболее вероятный путь гамма-переходов из второго возбужденного состояния ядра 24 Mg.(См.з.8) Определить мультипольности излучаемых гамма-квантов.
  10. Низшее возбужденное состояние ядра О-17 имеет спин и четность 1/2+. Указать конфигурацию этого состояния. Найти мультипольность и четность гамма-кванта, излучаемого при переходе из этого состояния в основное состояние ядра О-17.
  11. Определить орбитальный момент дейтрона, вылетающего в результате реакции 13С + p → 12C + 2H. Орбитальный момент протона равен 0.
  12. Определить активность изотопа 32Р, возникающего в результате облучения 1 г фосфора в течение 1 суток в потоке тепловых нейтронов 1012 см-2сек-1. Эффективное сечение активации фосфора равно 0.19 барн. Период полураспада Р-32 равен 14 суткам.
  13. Оценить увеличение эффективного сечения нейтронной активации при снижении в замедлителе кинетической энергии нейтронов от 5 МэВ до энергии, соответствующей тепловому равновесию.
  14. Определить кинетическую энергии альфа-частицы в альфа-распаде полония 210 Po.
  15. При флюорографии доза облучения организма составляет около 8 миллиГрей. Оценить эквивалентную дозу в бэр и Зв и сравнить с предельно допустимой дозой для населения (0.5 бэр/год = 0.005 Зв/год).

Содержние  Продолжение  

На головную страницу

 
Top.Mail.Ru