Модель оболочек является в настоящее время наиболее развитой и успешной из ядерных моделей. С ее помощью удается понять, почему для некоторых ядер удельные энергии связи и, особенно, энергии отделения нуклонов превышают те же величины для ядер с близкими значениями Z и А. Ядра, для которых этот эффект проявляется особенно ярко - т.е. ядра, значительно более устойчивые, чем их “соседи”, - называются магическими ядрами. У этих ядер числа протонов Z либо числа нейтронов N = А- Z равны одному из следующих чисел: 2, 8, 20, 28, 50, 82, 126 - т.н. магическим числам. Ядра, у которых и число протонов и число нейтронов - магические числа, называются дважды магическими и обладают особой устойчивостью. Однако и ряд других ядер, например, среди легких ядер , ядра 12С, 28Si также имеют значительно большие, чем соседние ядра, значения энергий отделения нуклонов. Приведем для иллюстрации значения удельных энергий связи и энергий отделения протона и нейтрона от некоторых ядер с А = 12, 13 и 16:
| Ядро | 12C | 13C | 13N | 16O |
| Ebind/A, МэВ | 7.67 | 7.45 | 7.22 | 7.96 |
| En | 18.7 | 4.95 | 20.1 | 15.66 |
| Ep | 15.9 | 17.4 | 1.9 | 12.13 |
Из таблицы видно, что хотя удельная энергия связи ядра
12С меньше, чем у дважды магического ядра 16О, энергии
отделения протонов и нейтронов для первого выше. Этот факт и аналогичные ему
являются следствием оболочечной структуры ядра. Очень важным достижением ядерной
модели оболочек также является теоретическое объяснение значений спинов и
четностей основного и возбужденных состояний ядер.
Оболочечная модель ядра представляет собой приложение
квантовой механики к системе нуклонов - ядру. Поскольку основы квантовой
механики в весеннем семестре 3 курса только начинают изучаться студентами, в дополнении дано изложение некоторых положений квантовой
механики применительно к проблеме описания ядерных оболочек.
Модель ядерных оболочек основана на решении уравнения
Шредингера для нуклона в потенциале
|
(11.1) |
Для того, чтобы понять роль спин-орбитального члена в потенциале (11.1), рассмотрим, какие значения может принимать полный момент нуклона j.
|
(11.2) |
Таким образом, полный момент нуклона может принимать два значения. Решения у.Ш. для энергий нуклона в потенциале (3.14) имеют следующий вид:
Enlj = |
(11.3) |
Двум значениям момента нуклона j = l + 1/2 и j = l -1/2 соответствуют разные
вклады в энергию состояния от спин-орбитального взаимодействия. (Схема уровней
легких ядер в потенциальной яме (11.1) показана на рис.11.1)
Прежде, чем рассчитать вклад от спин-орбитального
взаимодействия в одночастичную энергию, выясним, какие квантовые числа
характеризуют состояния нуклона в потенциале (11.1). Квантовые числа,
характеризующие состояния любой квантовой системы - т.н. хорошие квантовые числа - соответствуют собственным
значениям операторов тех физических величин, которые сохраняются в данном
потенциале. В квантовой механике доказывается, что для сохранения физической
величины необходимо, чтобы ее оператор коммутировал с гамильтонианом данной
квантовой системы. Для гамильтониана без
спин-орбитального члена хорошими квантовыми числами являются
следующие:
E, P (parity), l, s, ml, ms
Полный момент нуклона и проекция полного момента jz = lz + sz тоже сохраняются. Но для гамильтониана со спин-орбительным взаимодействием ситуация меняется - проекции орбитального и спинового моментов нуклонов не сохраняются! ( Операторы проекций орбитального и спинового моментов не коммутируют с гамильтонианом) Однако проекция полного момента на выделенную ось сохраняется. Хорошими квантовыми числами в этом случае гамильтониана с потенциалом (11.1) являются:
E, P, l, s, j, mj
Полученные нами выше волновые функции нуклонов представляют собой полную систему функций. Поэтому волновые функции, являющиеся решениями у.Ш. в потенциале со спин-орбитальным взаимодействием, можно разложить по этой системе функций:
|
(11.4) |
Суммирование в (11.4) происходит по всем возможным значениям проекций орбитального и спинового моментов нуклона. Поскольку mj = ml + ms а проекций спина нуклона всего две, в сумму входят не более двух членов. Коэфициенты разложения (11.4) называются коэфициентами Клебша-Гордона. Сумма их квадратов равна 1.
| Задача 11.1. Определить, сколько нуклонов может находиться на низшем по энергии уровне в потенциале гармонического осциллятора. Какое ядро соответствует такой схеме? |
Низшее по энергии состояние энергии в (11.3) соответствует
значениям квантовых чисел ![]() = 0, n = 0,
l = 0. Вклад спин-орбитального члена равен нулю, поскольку равен нулю
орбитальный момент l. Поэтому
= 0, n = 0,
l = 0. Вклад спин-орбитального члена равен нулю, поскольку равен нулю
орбитальный момент l. Поэтому
E00 = 3![]()
![]() /2
/2
По сложившейся в европейской физике традиции, ядерная
конфигурация с данными n и l обозначается как (n+1)lj, причем вместо
цифровых значений l используются буквеннные (s,p,d,f,g,h,i …).
Низшему состоянию нуклона соответствует конфигурация 1s. В
этом энергетическом состоянии может находиться не более 4 нуклонов - 2 протона с
противоположными значениями проекции спина на ось и 2 нейтрона в таких же
состояниях. Таким образом, модель оболочек дала объяснение первому из магических
чисел и существованию особо устойчивого дважды магического ядра гелия.
![]()
| Задача 11.2. Доказать, что вклад |
Для расчета вида вклада спин-орбитального члена необходимо найти величину матричного элемента
|
(11.5) |
Поскольку ![]() .
.
Здесь оператор спин-орбитального взаимодействия выражен через собственные
операторы волновой функции нуклона.
Вклад спин-орбитального взаимодействия в энергию нуклона в потенциальной яме
(11.1) равен
|
(11.6) |
Этот вклад в энергию нуклона расщепляет энергию уровня с данными l и s на два уровня с j = l + 1/2 и j = l - 1/2. Сравнение теоретического результата и экспериментальных данных (см. далее ) показало, что в ядре величина а в (11.1) отрицательна, поэтому
|
(11.7) |
Т.е. уровни с большим значением полного момента нуклона сдвигаются вниз
относительно энергии
E = ![]()
![]() (2n + l + 3/2),
а уровни с меньшим значением j (но теми же l ,s) сдвигаются вверх по энергии.
(2n + l + 3/2),
а уровни с меньшим значением j (но теми же l ,s) сдвигаются вверх по энергии.
Полученных выше результатов достаточно, чтобы разобраться в
заполнении оболочек для большинства ядер с A < 41.
| Задача 11.3. Сколько нуклонов может находиться в
состоянии |
Рассмотрим заполнение энергетических уровней для оболочки ![]() =1.Состояние с
=1.Состояние с ![]() =2n + l = 1
может иметь только l = 1. Это - в принятой системе обозначений - 1pj
конфигурация. Полный момент нуклона с l = 1 принимает значения 3/2 и 1/2. Низшей
по энергии является конфигурация 1p3/2. В этом состоянии может
находиться столько нейтронов, сколько имеется различных значений проекции
полного момента 3/2, т.е. 4. На этом же уровне (или подоболочке) может
находиться 4 протона. Таким образом, заполненная подоболочка 1p3/2
содержит 8 нуклонов. Ядро, у которого заполнена оболочка с
=2n + l = 1
может иметь только l = 1. Это - в принятой системе обозначений - 1pj
конфигурация. Полный момент нуклона с l = 1 принимает значения 3/2 и 1/2. Низшей
по энергии является конфигурация 1p3/2. В этом состоянии может
находиться столько нейтронов, сколько имеется различных значений проекции
полного момента 3/2, т.е. 4. На этом же уровне (или подоболочке) может
находиться 4 протона. Таким образом, заполненная подоболочка 1p3/2
содержит 8 нуклонов. Ядро, у которого заполнена оболочка с ![]() = 0 и
подоболочка 1p3/2, имеет в основном состоянии 12 нуклонов - 6
протонов и 6 нейтронов, т.е. это ядро 12С. Конфигурация основного
состояния этого ядра часто обозначается как |1s1/2>4 |1p3/2>8
= 0 и
подоболочка 1p3/2, имеет в основном состоянии 12 нуклонов - 6
протонов и 6 нейтронов, т.е. это ядро 12С. Конфигурация основного
состояния этого ядра часто обозначается как |1s1/2>4 |1p3/2>8
Заполнение следующей подоболочки 1p1/2 происходит по тем
же правилам. Поскольку число состояний равно удвоенному числу проекций полного
момента нуклона, на подоболочку 1p1/2 можно поместить не более 4
нуклонов. Таким образом, полностью заполненная оболочка с ![]() = 1
имеет две подоболочки с 8 и 4 нуклонами, т.е. заполненная оболочка имеет 12
нуклонов, что соответствует дважды магическому ядру 16О. Конфигурация
его основного состояния может быть изображена как 1s1/2>4 |1p3/2>8 |
1p1/2>4
= 1
имеет две подоболочки с 8 и 4 нуклонами, т.е. заполненная оболочка имеет 12
нуклонов, что соответствует дважды магическому ядру 16О. Конфигурация
его основного состояния может быть изображена как 1s1/2>4 |1p3/2>8 |
1p1/2>4
| Задача 11.4. Провести заполнение оболочки с |
Для ![]() = 2 = 2n + l существуют следующие возможности: n = 0, l = 2 (1d - конфигурации)
и n = 1, l = 0 (2s - конфигурация ). В первом случае величине полного момента
j = l + 1/2 = 5/2 соответствует низшая по энергии подоболочка 1d5/2.
В этой подоболочке может находиться не более 2(2 j + 1) = 12 нуклонов. Эта
подоболочка находится выше по энергии, чем оболочки с
= 2 = 2n + l существуют следующие возможности: n = 0, l = 2 (1d - конфигурации)
и n = 1, l = 0 (2s - конфигурация ). В первом случае величине полного момента
j = l + 1/2 = 5/2 соответствует низшая по энергии подоболочка 1d5/2.
В этой подоболочке может находиться не более 2(2 j + 1) = 12 нуклонов. Эта
подоболочка находится выше по энергии, чем оболочки с ![]() = 0 и
= 0 и ![]() = 1, на
которых находится 16 нуклонов ( 8 протонов + 8 нейтронов). Ядро с заполненными
= 1, на
которых находится 16 нуклонов ( 8 протонов + 8 нейтронов). Ядро с заполненными ![]() = 0 и
= 0 и ![]() = 1
оболочками и заполненной подоболочкой 1d5/2 имеет 14
протонов и 14 нейтронов - это 28Si. Следующей по энергии является 2s1/2
подоболочка с 4 нуклонами. Ядру, в котором, помимо оболочек с
= 1
оболочками и заполненной подоболочкой 1d5/2 имеет 14
протонов и 14 нейтронов - это 28Si. Следующей по энергии является 2s1/2
подоболочка с 4 нуклонами. Ядру, в котором, помимо оболочек с ![]() = 0
и
= 0
и ![]() = 1,
заполнены две подоболочки 1d5/2 и 2s1/2, соответствует
ядро 32S. Наконец, при заполнении последней подоболочки с
j = l-1/2=3/2 , т.е. 1d3/2
, оболочка с
= 1,
заполнены две подоболочки 1d5/2 и 2s1/2, соответствует
ядро 32S. Наконец, при заполнении последней подоболочки с
j = l-1/2=3/2 , т.е. 1d3/2
, оболочка с ![]() = 2
оказывается замкнутой. Этой конфигурации соответствует дважды магическое ядро
40Са. Конфигурация его основного состояния
= 2
оказывается замкнутой. Этой конфигурации соответствует дважды магическое ядро
40Са. Конфигурация его основного состояния
|1s1/2>4 |1p3/2>8| 1p1/2>4 | 1d5/2>12
|2s1/2>4 |1d3/2>4.
Нами была рассмотрена простейшая версия ядерной модели оболочек –
одночастичная модель оболочек без учета кулоновского взаимодействия между
протонами. Эта модель дает неплохие результаты для легких ядер, где кулоновское
взаимодействие не играет важной роли. Для ядер с A>40 энергию отталкивания
протонов уже нельзя не учитывать при модельном заполнении оболочек. Однако,
прежде, чем рассмотреть ядра с A>40, обсудим проблему спинов и четностей ядер.
Спины и четности ядер в модели оболочек
Суммарный момент системы одинаковых нуклонов, заполняющих
любую подоболочку, равен 0 независимо от квантовых чисел подоболочки и числа
(2j + 1) заполняющих ее нуклонов (нейтронов или протонов). Это важное правило
является следствием того факта, что среди заполняющих подоболочку (2j + 1)
одинаковых нуклонов будут обязательно находиться нуклоны с равными по абсолютной
величине, но разными по знаку проекциями полного момента нуклона на выделенную
ось. Такие пары одинаковых нуклонов имеют суммарный полный момент, равный 0.
Поэтому суммарные моменты импульсов как нейтронов, так и протонов на заполненной
подоболочке равны 0. По этой причине и спины основных состояний всех ядер с
заполненными оболочками или подоболочками равны 0.
Экспериментально доказано, что равны нулю спины основных
состояний всех четно-четных ядер, т.е. как ядер с заполненными подоболочками или
оболочками, так и ядер, у которых на подоболочке находятся по четному числу
протонов или нейтронов. Объяснение этого экспериментального факта – наличие в
ядерных взаимодействиях не учтенных в предыдущем изложении одночастичной модели
оболочек сил – т.н. сил спаривания.
Необходимо отметить, что замена всех действующих между нуклонами сил
самосогласованным потенциалом со спин-орбитальным членом (например,(11.1))
является довольно грубым модельным приближением. Не учтенные в (11.1) силы
называются силами остаточного взаимодействия
и играют важную роль в формировании свойств ядер. Важнейшим компонентом сил
остаточного взаимодействия являются силы спаривания. Действие сил спаривания
приводит к тому, что для любых двух одинаковых нуклонов наиболее выгодным по
энергии (т.е. низшим) состоянием будет состояние с полным моментом 0 или, иначе
говоря, с противоположными направлениями проекций полного момента на выделенную
ось. Для всех четных по Z и по N ядер это приводит к значениям спина J = 0 в
основном состоянии.
Пространственная четность основных состояний всех
четно-четных ядер положительна. Четность – мультипликативное квантовое число.
(См. семинар 4) Поскольку собственная четность нуклонов +1, то пространственная
четность ядерного состояния определяется произведением четностей волновых
функций. Для любого состояния нуклона с квантовыми числами l,s,j
|
(11.8) |
Для ядра как системы A нуклонов пространственная четность есть произведение четностей (11.8) всех нуклонов:
|
(11.9) |
Для всех заполненных оболочек и подоболочек четность
положительна, поскольку для них в показателе степени (11.9) будет стоять четное
число. Поэтому и у всех четно-четных ядер в основном состоянии четность
положительна.
Принято указывать одновременно спин и четность состояния
системы в виде JP. (Здесь P является не степенью, а символом четности
состояния). Для всех четно- четных ядер в основном состоянии JP = 0+.
Спин и четность основного состояния ядра с одним нуклоном сверх
замкнутой оболочки или подоболочки определяется моментом и четностью
неспаренного нуклона. Спин ядра является векторной суммой спина ядра с А
нуклонами и неспаренного нуклона, но спин ядра с А нуклонами 0, если это ядро с
замкнутой оболочкой или подоболочкой.
Четность основного состояния ядра с одним нуклоном сверх
замкнутой оболочки или подоболочки определена четностью (-1)l
неспаренного нуклона.
PA+1 = PAPl = (+1)(-1)l = (-1)l. |
(11.10) |
Рассмотрим теперь ядра, у которых до заполненной оболочки или подоболочки недостает одного нуклона. Эти ядра часто называют ядрами с одной “дыркой” относительно замкнутой подоболочки или оболочки. У всех таких ядер спин и четность определяются моментом и четностью “отсутствующего” нуклона, т.е. моментом и четностью “дырки”. Действительно,
|
(11.11) |
Здесь момент недостающего нуклона обозначен как jh, где h соответствует обозначению “дырки” “hole”. Аналогично (11.10) получим для четности ядра с одной “дыркой”
PA = PA-1Ph = +1; PA-1 = Ph. |
(11.12) |
| Задача 11.5. Определить по модели оболочек спины и четности ядер 13С и 17О в основных состояниях. Сравнить результат с экспериментальными данными. |
Ядро 13С в основном состоянии имеет следующую
конфигурацию нуклонов 1s1/2>4 |1p3/2>8 |
1p1/2>1n.
Неспаренный нейтрон имеет полный момент 1/2. Следовательно, спин ядра 13С
в основном состоянии 1/2. Четность основного состояния 13С определена
(см.(11.10)) как (-1)l. Поскольку неспаренный нейтрон находится в 1р
оболочке, четность отрицательна. Итак, для ядра 13С JP = (1/2)-,
что объясняет экспериментальный результат.
Для ядра 17О нуклонная конфигурация основного
состояния |1s1/2>4 |1p3/2>8| 1p1/2>4 | 1d5/2>1n.
Отсюда спин и четность его основного состояния JP = (5/2)+,
что соответствует экспериментальной величине.
| Задача 11.6. Определить спины и четности основных состояний ядер 3He и 11B. |
Ядро 3He соответствует нейтронной “дырке” в
дважды магическом ядре 4Не. Соответственно, его спин и четность
соответствуют моменту 1/2 и четности (-1)l = + 1 недостающего
нейтрона. Следовательно JP = (1/2)+.
Для ядра 11B спин и четность определяет недостающий до
замкнутой подоболочки протон в состоянии 1р3/2, соответственно у ядра
11B - JP = (3/2)-.
Следует обратить внимание на важное правило: как частицы над
замкнутой конфигурацией, так и дырки относительно нее могут рассматриваться
одинаковым образом. Иногда и те и другие в научной литература называют “квазичастицами”.
Одночастичная модель оболочек объясняет значения спинов и
четностей ядер с одной “квазичастицей” сверх замкнутой конфигурации, т.е.
полностью заполненной оболочки или подоболочки. Часто эту модель применяют для
того, чтобы рассмотреть спины и четности ядер, у которых сверх замкнутой
конфигурации имеется более одной квазичастицы. Рассмотрим один из таких примеров
как задачу.
| Задача 11.7. Определить спин и четность основного состояния ядра 7Li. |
Конфигурация основного состояния этого ядра 1s1/2>4 |1p3/2>3
причем сверх замкнутой оболочки дважды магического ядра 4Не в
1р оболочке находится два нейтрона и один протон. Два нейтрона за счет сил
спаривания имеют полный суммарный момент 0, поэтому спин и четность ядра
определены моментом и четностью неспаренного протона, т.е. JP=(3/2)-.
Этот модельный результат совпадает с экспериментальным.
Ядра с двумя протонами либо двумя нейтронами сверх замкнутой
оболочки ( или подоболочки) - четно-четные ядра с JP=0+.
Но ядра с одном протоном и одном нейтроном сверх замкнутой подоболочки -
нечетно-нечетные. Для двух разных нуклонов на незамкнутой “валентной” подоболочке принцип Паули не
препятствует тому, чтобы они имели одинаковые проекции момента на выделенную ось
и, соответственно, суммарный момент не равный нулю. Например, ядро 14С
с двумя нейтронами над замкнутой подоболочкой 1р3/2 (ядром 12С)
имеет в основном состоянии JP = 0+
и конфигурацию нуклонов |1s1/2>4|1p3/2>8|
1p1/2>2n, а ядро 14N имеет в
основном состоянии конфигурацию |1s1/2>4|1p3/2>8|
1p1/2>1n | 1p1/2>1p
и спин и четность этого состояния JP = 1+. Таким
образом, моменты протона и нейтрона в валентной подоболочке 14 N
параллельны и сложились в 1.(Напомним, что спин системы протон- нейтрон , т.е.
дейтрона, также 1). Низшее по энергии - т.е. основное - состояние ядер с
протонной и нейтронной “дырками” относительно замкнутой подоболочки - ядра
12С в основном состоянии - также имеет спин, соответствующий максимально
возможному моменту пары квазичастиц. Например, ядро 10В имеет
конфигурацию основного состояния 1s1/2>4|1p3/2>6 = |1p3/2>-1n|1p3/2>-1p![]() (12C)>.
При этом моменты двух квазичастиц - протонной и нейтронной “дырок” -
складываются в максимальный суммарный момент 3. Отсюда для ядра 10В JP = 3+.
(12C)>.
При этом моменты двух квазичастиц - протонной и нейтронной “дырок” -
складываются в максимальный суммарный момент 3. Отсюда для ядра 10В JP = 3+.
| Задача 11.8. Найти спин и четность ядра 26Al в основном состоянии и сравнить результат с экспериментальным. |
Ядро 26Al в основном состоянии соответствует протонной и нейтронной “дыркам” относительно ядра 28Si:
![]()
Сумма моментов протонной и нейтронной “дырок” равна 5. JP(26Al)
= 5+.
Низшее по энергии состояние системы нуклонов с замкнутыми
оболочками или подоболочками можно считать состоянием физического вакуума. (В
предыдущем примере неявным образом физическим вакуумом было объявлено основное
состояние ядра 28Si). В дальнейшем это представление будет очень
удобным при рассмотрении возбужденных состояний ядер.
Если при возбуждении ядра, т.е. при поглощении ядром
некоторой энергии, эта энергия передается одному нуклону над замкнутой оболочкой
или подоболочкой, этот неспаренный нуклон будет переходить на более высокие
уровни энергии, а остальные нуклоны ядра (т.н. кор) будут оставаться в прежних
невозбужденных состояниях. Такие возбуждения называются одночастичными. В
спектрах возбуждения ядер с одним нуклоном над замкнутой оболочкой или
подоболочкой можно выделить уровни, соответствующие одночастичным возбуждениям.
Задание 4
- Определить энергии связи и удельные энергии связи ядер 4He,7Li,12C, 13C, 27Al.
- Для ядер задачи 1 рассчитать энергии отделения нейтрона и протона.
- Вывести формулу, связывающую энергию связи и избыток массы М-А ядра.
- Сравнить энергии отделения протона, нейтрона и альфа-частицы от ядра 16O.
- При какой кинетической энергии частицы ее длина волны становится равной диаметру ядра 27Al? Рассмотреть два случая: а) электрон; b) нейтрон.
- Найти кинетические энергии протона и электрона с приведенными длинами волн 1 Fm.
- Определить максимальную длину волны гамма-кванта в реакции
 + 12С
+ 12С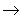 11С
+ n.
11С
+ n. - Найти возможные значения полного момента атома, если спин ядра атома равен 5/2, а момент электронной оболочки составляет 3/2. Для каждого значения полного момента j указать возможные значения проекций моментов mj.
- Рассчитать магнитный момент системы нейтрон-протон в состоянии 3S1. Сравнить результат с экспериментально найденным значением магнитного момента дейтрона (0.86 ядерных магнетонов).
- Рассчитать электрический квадрупольный момент сферически симметричного ядра или частицы.
- Четность дейтрона равна +1. Спин дейтрона равен 1. Найти возможные значения орбитального момента системы протон-нейтрон в дейтроне.
- Найти значения изоспина ядер 208 Pb, 197Au и 209Bi в основных состояниях.
- Рассчитать величину кинетической энергии, выделяющейся в результате
термоядерной реакции
2H + 3H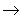 4He
+ 1n.
4He
+ 1n. - В рамках капельной модели ядра рассчитать вклады отдельных членов в суммарную энергию связи для двух ядер: с А>200 и A<100.
- На схеме уровней нуклона в потенциале трехмерного осциллятора со спин-орбитальным взаимодействием изобразить конфигурационные структуры основных состояний ядер 4He,12C и 16O.
- Перечислить квантовые числа нуклонов, формирующих ядра задачи 16. Показать на этих примерах выполнение принципа Паули.
- В одночастичной оболочечной модели получить спины и четности основных состояний следующих ядер:5He, 13C, 17O, 17F, 29Si, 33S, 3He, 11C, 15N, 27Al. Cравнить результат с экспериментальными данными [4].
- Указать конфигурационную структуру ядер 57Ni, 58Ni, 59Ni, 60Ni. Обосновать результат сравнением с экспериментальными данными о спинах и четностях этих ядер.