В физике микромира характеристиками вероятности процессов
взаимодействия частиц и ядер являются дифференциальное и полное эффективные
сечения реакций.
Рассмотрим поток частиц А, падающих на мишень и вступающих во
взаимодействие с частицами мишени В. Результатом реакции может быть как
появление частиц А и В с другими кинематическими характеристиками, так и
возникновение новых частиц.
Дифференциальное эффективное сечение реакции в системе покоя
мишени определяется как
|
(3.1) |
Здесь ![]() -угол рассеяния, dN(
-угол рассеяния, dN(![]() )/d
)/d![]() - число
частиц, вылетевших под этим углом в единицу времени ( в секунду) в единичном
телесном угле
- число
частиц, вылетевших под этим углом в единицу времени ( в секунду) в единичном
телесном угле ![]() . I - величина
потока частиц А, падающих на мишень. n - полное число частиц В в мишени,
находящихся в пучке.
. I - величина
потока частиц А, падающих на мишень. n - полное число частиц В в мишени,
находящихся в пучке.
Полное (или интегральное) эффективное сечение реакции
является интегралом от (3.1) по углу рассеяния:
|
(3.2) |
Размерность эффективного сечения реакции - см2.
Поскольку эффективные сечения процессов микромира в единицах см2 представляют
собой очень малые величины, они измеряются, как правило, в единицах 1 барн =
1 б =10-24 см2.
Серия экспериментов по измерению эффективных сечений
рассеяния ![]() -частицы на ядрах
была проведена Резерфордом. Им было показано, что практически вся масса атома сосредоточена
в ядре, линейные размеры которого примерно в 105 раз меньше размеров
атома. Для дифференциального сечения рассеяния
-частицы на ядрах
была проведена Резерфордом. Им было показано, что практически вся масса атома сосредоточена
в ядре, линейные размеры которого примерно в 105 раз меньше размеров
атома. Для дифференциального сечения рассеяния ![]() -частицы на ядре
с зарядом Ze им была получена формула:
-частицы на ядре
с зарядом Ze им была получена формула:
|
(3.3) |
| Задача 3.1. Рассчитать
дифференциальное эффективное сечение рассеяния |

![]() 0.34.10-24
см2/стер. = 0.34 барн/стер.
0.34.10-24
см2/стер. = 0.34 барн/стер.
Здесь для упрощения процедуры расчета использована константа
электромагнитного взаимодействия ![]() е
= e2/
е
= e2/![]() c
=1/137
c
=1/137![]() c
c![]() 200 МэВ.Фм.
200 МэВ.Фм.
| Задача 3.2. Рассчитать дифференциальное
эффективное сечение рассеяния |
Расчет аналогичен расчету предыдущей задачи.

Следует отметить, что формула Резерфорда в виде (3.3)
справедлива лишь при энергиях ![]() -частиц,
не превышающих примерно 20 МэВ. При более высоких энергиях в формулу (3.3)
должен быть введен еще один множитель – формфактор, связанный с внутренней
структурой ядра-рассеивателя.
-частиц,
не превышающих примерно 20 МэВ. При более высоких энергиях в формулу (3.3)
должен быть введен еще один множитель – формфактор, связанный с внутренней
структурой ядра-рассеивателя.
Диаграммы Фейнмана
В квантовой теории существует удобный метод описания и
расчета процессов взаимодействия частиц, основанный на использовании
диаграмм Фейнмана
(ДФ).
В диаграммах Фейнмана физическому процессу сопоставляется его
графическая схема. Каждой участвующей в процессе частице соответствует линия.
Обычно линии фермионов - тонкие прямые линии. Линии бозонов изображают либо
волнистыми, либо штриховыми прямыми. (Частицам, не являющимся по современным
представления бесструктурными, иногда сопоставляются на диаграммах либо толстые
линии, либо пучки параллельных линий).
Диаграмма Фейнмана задает алгоритм вычисления амплитуды
вероятности процесса. Каждому элементу диаграммы соответствуют определенные
множители в расчете амплитуды вероятности. Линии, один из концов которых
свободен, соответствуют свободным частицам. В расчете амплитуды вероятности этим
линиям отвечают волновые функции частиц. Квадрат модуля амплитуды вероятности
определяет вероятность процесса
Линии на ДФ могут описывать распространение как частиц, так и
античастиц: направление стрелок на линиях античастиц противоположно направлениям
стрелок на линиях частиц.
Взаимодействие частиц на диаграмме изображается вершиной (или
узлом), в котором сходятся две фермионных и одна бозонная линии. Каждой вершине
в амплитуде вероятности процесса соответствует константа взаимодействия. В
случае электромагнитных процессов вершинной константой является величина
( |
(3.4) |
В системе единиц ![]() = c = 1
= c = 1 ![]() (
(![]() e)1/2
= e. Величина квадрата этой константы при не очень высоких энергиях равна
e)1/2
= e. Величина квадрата этой константы при не очень высоких энергиях равна
|
(3.5) |
Частицы, изображенные линиями, начинающимися и
кончающимися в вершинах - это т.н.
виртуальные частицы. Линиям виртуальных
частиц в расчете ДФ сопоставляются функции распространения этих частиц,
называемые пропагаторами. Именно виртуальные частицы
ответственны за реализацию взаимодействия частиц. Для процессов взаимодействия,
которые и осуществляются путем рождения и поглощения виртуальных частиц,
характерно, что в течение интервала времени взаимодействия ![]() t
имеет место отклонение
t
имеет место отклонение ![]() E энергии виртуальной частицы от ее точного
значения, соответствующего закону сохранения, причем
E энергии виртуальной частицы от ее точного
значения, соответствующего закону сохранения, причем
|
(3.6) |
(соотношение неопределенности Гейзенберга для энергии и времени)
Для виртуальных частиц
E2 |
(3.7) |
Следует подчеркнуть, что в целом для всего процесса законы
сохранения выполняются точно, в частности, полная энергия частиц до
взаимодействия равна полной энергии частиц после взаимодействия.
На рис. 3.1 изображена диаграмма Фейнмана для рассеяния
фотона на электроне. (Вектор времени направлен слева направо). Перемена
направлений на фермионной линии дает диаграмму Фейнмана для рассеяния фотона на
позитроне. Диаграммы Фейнмана обладают замечательными свойствами: если на рис.1
направить вектор времени снизу вверх
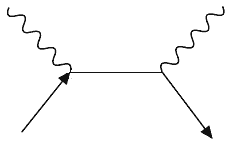
Рис.3.1
(или, сохраняя направление вектора времени, повернуть ее на 900),
диаграмма будет изображать двухфотонную аннигиляцию ![]()
![]() +
+ ![]() .
.
Диаграммы Фейнмана не только являются иллюстрацией реакций с
частицами, но и позволяют - даже без проведения точного расчета - сделать
некоторые важные оценки соотношения вероятностей процессов. Например, с их
помощью легко доказать доминирующую роль низших по числу вершин (или количеству
виртуальных частиц) диаграмм в электромагнитных взаимодействиях.
Рассмотрим в качестве примера рассеяние электрона на
электроне. Квантом электромагнитного взаимодействия является виртуальный фотон.
На рисунке 3.2 показана обобщенная диаграмма этого процесса,
которая может быть представлена как сумма диаграмм с разным количеством
вершин.
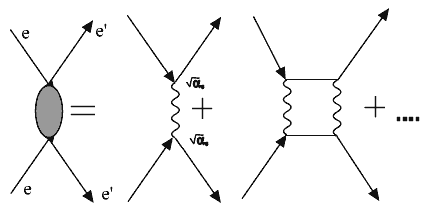
Рис.3.2
Поскольку взаимодействие электромагнитное, каждой вершине соответствует константа электромагнитного взаимодействия
(![]() e)1/2
= e/(
e)1/2
= e/(![]() c)1/2.
c)1/2.
Первая из диаграмм Фейнмана, дающая вклад в процесс
рассеяния электрона на электроне, имеет две вершины, ее вклад в амплитуду
вероятности процесса (матричный элемент процесса M) пропорционален произведению
квадрату константы (3.4): M ~ ![]() e.
e.
Вероятность процесса, характеризуемая величиной
эффективного сечения, пропорциональна квадрату матричного элемента ![]() ~ M2,
соответствующего отдельной диаграмме. Поэтому вклад первой из диаграмм в правой
части рис.3.2 в вероятность рассеяния пропорционален величине
~ M2,
соответствующего отдельной диаграмме. Поэтому вклад первой из диаграмм в правой
части рис.3.2 в вероятность рассеяния пропорционален величине ![]() 2
2 ![]() (1/137)2.
(1/137)2.
Вклады диаграмм более высокого порядка, т.е. с большим числом
вершин, много меньше вклада этой первой диаграммы. Например, вторая из диаграмм
Фейнмана в правой части рис.3.2, дает в вероятность процесса рассеяния электрона
на электроне вклад, пропорциональный ![]() 4
4 ![]() (1/137)4.
(Следует отметить, что “константы взаимодействия”, строго
говоря, не постоянны: они зависят от энергии взаимодействия.
Однако в области энергий взаимодействия E<10 ГэВ этим эффектом можно пренебречь)
(1/137)4.
(Следует отметить, что “константы взаимодействия”, строго
говоря, не постоянны: они зависят от энергии взаимодействия.
Однако в области энергий взаимодействия E<10 ГэВ этим эффектом можно пренебречь)
| Задача 3.3. Оценить отношение вероятностей процессов трехфотонной и двухфотонной аннигиляции пары электрон-позитрон. |
Процессы e+ + e-![]()
![]() +
+ ![]() и e+ + e-
и e+ + e-![]()
![]() +
+ ![]() +
+ ![]() в низшем порядке по константе электромагнитного взаимодействия могут быть
представлены ДФ на рис.3.3.
в низшем порядке по константе электромагнитного взаимодействия могут быть
представлены ДФ на рис.3.3.
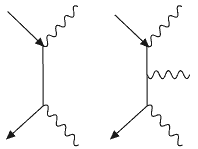
Рис.3.3
Для первого процесса с двумя вершинами вероятностьW1 ~ ![]() 2,
для второго W2 ~
2,
для второго W2 ~ ![]() 3.
Отношение вероятностей (W1/W2) ~ 137. Отметим, что первая
диаграмма соответствует распаду парапозитрония, т.е. состояния системы e+e-
с полным моментом количества движения J = 0 ( спины e+ и e-
антипараллельны). Вторая диаграмма отражает распад ортопозитрония - системы e+e-
с полным моментом количества движения J = 1.
3.
Отношение вероятностей (W1/W2) ~ 137. Отметим, что первая
диаграмма соответствует распаду парапозитрония, т.е. состояния системы e+e-
с полным моментом количества движения J = 0 ( спины e+ и e-
антипараллельны). Вторая диаграмма отражает распад ортопозитрония - системы e+e-
с полным моментом количества движения J = 1.
Рассмотрим рассеяние электрона на ядре с числом протонов Z.
Дифференциальное эффективное сечение рассеяния для этого процесса имеет вид:
|
(3.8) |
Здесь F – формфактор, зависящий от
плотности распределения заряда в ядре-мишени. Если рассеяние происходит на
частице, которую можно считать точечной, F = 1.
Дифференциальное сечение рассеяния электронов на точечном
заряде (формула Мотта) отличается от формулы Резерфорда множителем cos2![]() . Величины
резерфордовского и моттовского сечений пропорциональны квадрату константы
электромагнитного взаимодействия
. Величины
резерфордовского и моттовского сечений пропорциональны квадрату константы
электромагнитного взаимодействия ![]() e, как
это и следует из диаграмм Фейнмана этих процессов. Для формулы Резерфорда
доказательством этого факт является решение задачи 3.1. Для формулы Мотта
рассеяния электрона на ядре
e, как
это и следует из диаграмм Фейнмана этих процессов. Для формулы Резерфорда
доказательством этого факт является решение задачи 3.1. Для формулы Мотта
рассеяния электрона на ядре
|
(3.9) |
| Задача 3.4. Рассчитать дифференциальное эффективное сечение рассеяния электрона с кинетической энергией 10 МэВ на ядре Са-40. Угол рассеяния равен 600. |
Расчет сечения аналогичен проведенному в задаче 3.1 .
Результат отличается от полученного ранее множителем ![]() = 1/4.
= 1/4.
(d![]() (
(![]()
![]() )М
= 0.085 барн/стер.
)М
= 0.085 барн/стер.
| Задача 3.5. Обосновать справедливость применения формулы Мотта с F = 1 в задаче 3.4. |
Введение формфактора как в формулу Резерфорда, так и в формулу Мотта необходимо в тех случаях, когда длина волны рассеиваемой на ядре частицы меньше, чем диаметр ядра. Для ядра Са-40 диаметр равен приблизительно
2R![]() r0A1/3
r0A1/3![]() 2.1.3.3.4
Фм = 9 Фм.
2.1.3.3.4
Фм = 9 Фм.
Длина волны электрона с кинетической энергией 10 МэВ
![]() = 2
= 2![]()
![]() = 2
= 2![]()
![]() c/pc
c/pc![]() 125 Фм.
125 Фм.
Таким образом, применение формулы Мотта для рассеяния электрона на точечном заряде оправдано для электронов с кинетической энергией 10 МэВ.

 .
.
