2. Альфа-распад
Явление α-распада состоит в том, что атомные ядра
самопроизвольно испускают из основного состояния α-частицы
– ядра 4He. При этом массовое число ядра A уменьшается на
четыре единицы, а заряд ядра Z − на две единицы:
| (A,Z) → (A−4, Z−2) + 4He. |
(2.1) |
Периоды полураспада известных
α-радиоактивных ядер варьируются в
широких пределах. Так, изотоп вольфрама 182W имеет период полураспада
T1/2 > 8.3·1018 лет, а изотоп
протактиния 219Pa имеет
T1/2 = 5.3·10-8 c.
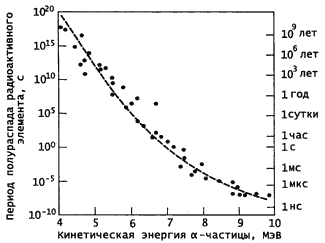
Рис. 2.1. Зависимость периода
полураспада радиоактивного элемента от кинетической энергии α-частицы естественно
радиоактивного элемента. Штриховая линия – закон Гейгера-Нэттола.
Для четно-четных изотопов зависимость
периода полураспада от энергии α-распада Qα описывается
эмпирическим законом Гейгера-Неттола
| lg T1/2 = A + B/√Qα, |
(2.2) |
где A и B – константы, слабо зависящие от Z. С учётом заряда ядра
Z связь между периодом полураспада T1/2 и энергией α-распада
может быть представлена в виде
| lg T1/2 = 1.61(ZEα-1/2
– Z2/3) + 28.9, |
(2.3) |
где Z −
заряд конечного ядра, период полураспада
T1/2 выражен в секундах, а энергия α-частицы Eα − в МэВ. На рис. 2.1 показаны
экспериментальные значения периодов полураспада для α-радиоактивных четно-четных изотопов (Z
изменяется от 74 до 106) и их описание с помощью соотношения (2.3).
Для нечетно-четных, четно-нечетных и
нечетно-нечетных ядер общая тенденция зависимости
lg T1/2 от Qα сохраняется,
но периоды полураспада в 2–100 раз больше, чем для четно-четных ядер с теми же
Z и Qα.
Для того чтобы происходил α-распад, необходимо, чтобы масса
исходного ядра M(A,Z) была
больше суммы масс конечного ядра
M(A-4, Z-2)
и α-частицы Mα:
| M(A,Z) > M(A-4, Z-2) + Mα. |
(2.4) |
В результате α-распада ядра (A,Z) в конечном состоянии образуются
два продукта распада: α-частица и ядро (A-4, Z-2). Поэтому энергия α‑частицы Eα имеет фиксированное
значение, определяемое законами сохранения энергии и импульса
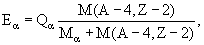 |
(2.5) |
где Qα = [M(A,Z) – M(A-4, Z-2) + Mα]c2 −
энергия α-распада.
Так как Mα << M(A-4, Z-2),
основная часть энергии α-распада уносится α‑частицей и лишь ≈ 2% − конечным ядром
(A-4, Z-2).
Энергетические спектры α-частиц многих радиоактивных элементов
состоят из нескольких линий (тонкая структура α-спектров). Причина появления тонкой
структуры α-спектра
− распад начального ядра (A,Z) на возбужденное состояние ядра (A-4, Z-2). Измеряя спектры α-частиц можно получить
информацию о природе возбужденных состояний
ядра (A-4, Z-2).
Для определения области значений А и
Z ядер,
для которых энергетически возможен α-распад, используют экспериментальные данные об
энергиях связи ядер. Зависимость энергии α-распада Qα от массового числа А
показана на рис. 2.2.
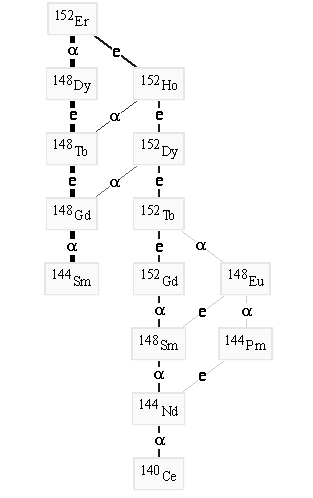
Из рис. 2.2 видно, что α-распад становится энергетически
возможным, начиная с А ≈ 140. В областях A = 140–150 и A ≈ 210 величина Qα
имеет отчетливые максимумы, которые обусловлены оболочечной структурой
ядра. Максимум при A = 140–150
связан с заполнением нейтронной оболочки с магическим числом N
=А – Z
=
82, а максимум при A ≈ 210 связан с заполнением
протонной оболочки при
Z = 82. Именно за счет оболочечной структуры атомного ядра
первая (редкоземельная) область α-активных ядер начинается с N = 82, а тяжелые α-радиоактивные ядра становятся
особенно многочисленными, начиная с Z = 82.
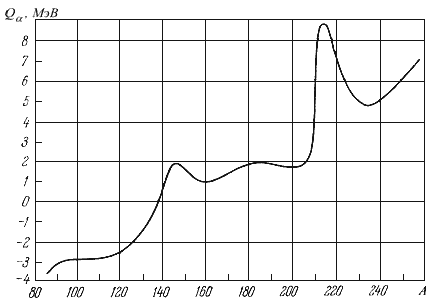
Рис. 2.2. Зависимость энергии α-распада от массового числа А.
Широкий диапазон периодов полураспада, а также большие значения этих периодов
для многих α-радиоактивных ядер объясняются тем, что α‑частица не может «мгновенно» покинуть ядро, несмотря на то,
что это энергетически выгодно. Для того чтобы покинуть ядро, α‑частица должна преодолеть потенциальный барьер − область на
границе ядра, образующуюся за счёт потенциальной энергии электростатического
отталкивания a-частицы и конечного ядра и сил притяжения
между нуклонами. С точки зрения классической физики α‑частица не может преодолеть потенциальный барьер, так как
не имеет необходимой для этого кинетической энергии. Однако квантовая механика
допускает такую возможность − α‑частица имеет
определённую вероятность пройти сквозь потенциальный барьер и покинуть ядро. Это квантовомеханическое явление называют «туннельным эффектом» или
«туннелированием». Чем больше высота и ширина барьера, тем меньше вероятность туннелирования, а период полураспада соответственно больше. Большой диапазон
периодов полураспада
α-излучателей объясняется различным сочетанием
кинетических энергий α-частиц и высот потенциальных
барьеров. Если бы барьера не существовало, то α‑частица покинула бы ядро за характерное ядерное
время ≈ 10-21 – 10-23 с.
Простейшая модель α-распада была предложена в 1928 году Г. Гамовым и независимо от него
Г. Герни и Э. Кондоном. В этой модели предполагалось, что α‑частица
постоянно существует в ядре. Пока α-частица находится в
ядре на нее действуют ядерные силы притяжения. Радиус их действия сравним с
радиусом ядра R. Глубина ядерного потенциала – V0.
За пределами ядерной поверхности при r > R потенциал является
кулоновским потенциалом отталкивания
V(r) = 2Ze2/r.
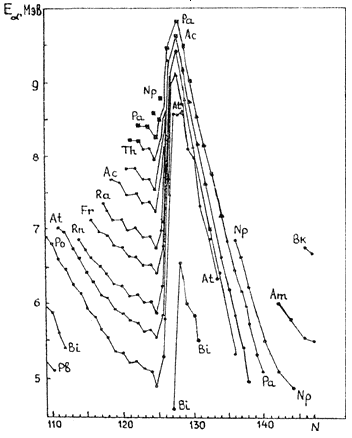
Рис. 2.3. Энергии α‑частиц Eα в зависимости от числа
нейтронов
N
в
исходном ядре. Линии соединяют изотопы одного и того же химического элемента.
Упрощенная схема совместного действия ядерного потенциала притяжения и
кулоновского потенциала отталкивания показана на рисунке 2.4. Для того, чтобы
выйти за пределы ядра α-частица с энергией Eα должна пройти сквозь потенциальный
барьер, заключенный в области от
R до Rc. Вероятность α-распада в основном определяется вероятностью D прохождения
α-частицы
через потенциальный барьер
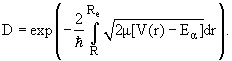
В рамках этой модели удалось объяснить сильную зависимость вероятности α‑распада от энергии
α-частицы.
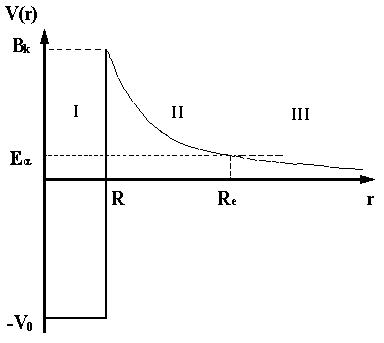
Рис. 2.4. Потенциальная энергия
α-частицы. Потенциальный барьер.
Для того чтобы рассчитать
постоянную распада λ, надо коэффициент прохождения α-частицы через потенциальный барьер
умножить, во-первых, на вероятность wα того, что α‑частица образовалась в ядре, и,
во-вторых, на вероятность того, что она окажется на границе ядра. Если α‑частица в ядре радиуса
R имеет скорость
v, то она будет подходить к
границе в среднем ≈ v/2R раз
в секунду. В результате для постоянной распада λ получается соотношение
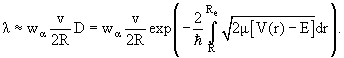 |
(2.6) |
Скорость α‑частицы в ядре можно оценить,
исходя из её кинетической энергии Eα + V0 внутри
ядерной потенциальной ямы, что даёт
v ≈ (0.1-0.2)с. Уже из этого
следует, что при наличии в ядре α‑частицы вероятность её пройти сквозь барьер D
<10-14 (для самых короткоживущих
относительно α‑распада тяжелых ядер).
Грубость оценки
предэкспоненциального множителя не очень существенна, потому что постоянная
распада зависит от него несравненно слабее, чем от показателя экспоненты.
Из формулы (2.6) следует, что
период полураспада сильно зависит от радиуса ядра
R, поскольку радиус
R входит не только
в предэкспоненциальный множитель, но и в показатель экспоненты, как предел
интегрирования. Поэтому из данных по α-распаду можно определять радиусы атомных ядер. Полученные таким путем
радиусы оказываются на 20–30% больше найденных в опытах по рассеянию электронов.
Это различие связано с тем, что в опытах с быстрыми электронами измеряется
радиус распределения электрического заряда в ядре, а в α-распаде измеряется расстояние
между ядром и α‑частицей, на котором перестают действовать ядерные силы.
Наличие постоянной Планка
в показателе экспоненты (2.6) объясняет сильную зависимость периода полураспада
от энергии. Даже небольшое изменение энергии приводит к значительному изменению
показателя экспоненты и тем самым к очень резкому изменению периода полураспада.
Поэтому энергии вылетающих α‑частиц сильно ограничены. Для
тяжелых ядер α‑частицы с энергиями выше 9 МэВ вылетают практически мгновенно, а с
энергиями ниже 4 МэВ живут в ядре так долго, что α-распад даже не удается зарегистрировать.
Для редкоземельных α-радиоактивных ядер обе энергии снижаются за счет уменьшения радиуса ядра
и высоты потенциального барьера.
На рис. 2.5 показана зависимость
энергии α-распада
изотопов Hf (Z = 72) от массового числа A в области массовых
чисел A = 156–185. В
таблице 2.1 приведены энергии α-распада, периоды полураспада и основные
каналы распада изотопов 156–185Hf. Видно как по мере увеличения
массового числа A уменьшается
энергия α-распада,
что приводит к уменьшению вероятности α-распада и увеличению вероятности β-распада (таблица 2.1).
Изотоп 174Hf, являясь стабильным изотопом (в естественной смеси
изотопов он составляет 0.16%), тем не менее распадается с периодом полураспада T1/2 = 2·1015 лет с испусканием
α‑частицы.
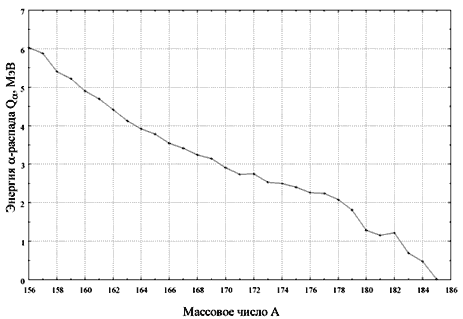
Рис. 2.5.
Зависимость энергии α-распада Qα изотопов
Hf (Z = 72)
от массового числа
A.
Таблица 2.1
Зависимость энергии α-распада Qα, периода полураспада
T1/2,
различных мод распада
изотопов H f (Z = 72) от массового числа
A
| Z |
N |
A |
Qα |
T1/2 |
Моды распада (%) |
| 72 |
84 |
156 |
6.0350 |
23 мс |
α (100) |
| 72 |
85 |
157 |
5.8850 |
110 мс |
α (86), е (14) |
| 72 |
86 |
158 |
5.4050 |
2.85 с |
α (44.3), е (55.7) |
| 72 |
87 |
159 |
5.2250 |
5.6 с |
α (35),
е (65) |
| 72 |
88 |
160 |
4.9020 |
13.6 с |
α (0.7), е (99.3) |
| 72 |
89 |
161 |
4.6980 |
18.2 с |
α (<0.13),
е (>99.87) |
| 72 |
90 |
162 |
4.4160 |
39.4 с |
α (<8·10-3),
е (99.99) |
| 72 |
91 |
163 |
4.1280 |
40.0 с |
α (<1·10-4),
е (100) |
|
72 |
92 |
164 |
3.9240 |
111 с |
е
(100) |
|
72 |
93 |
165 |
3.7790 |
76 с |
е
(100) |
|
72 |
94 |
166 |
3.5460 |
6.77
мин |
е
(100) |
|
72 |
95 |
167 |
3.4090 |
2.05
мин |
е
(100) |
|
72 |
96 |
168 |
3.2380 |
25.95
мин |
е
(100) |
|
72 |
97 |
169 |
3.1450 |
3.24
мин |
е
(100) |
|
72 |
98 |
170 |
2.9130 |
16.01
ч |
е
(100) |
|
72 |
99 |
171 |
2.7390 |
12.1 ч |
е
(100) |
|
72 |
100 |
172 |
2.7470 |
1.87 ч |
е
(100) |
|
72 |
101 |
173 |
2.5350 |
23.4 ч |
е
(100) |
|
72 |
102 |
174 |
2.4960 |
2·1015 л |
е
(100) |
|
72 |
103 |
175 |
2.4041 |
70 дн |
е
(100) |
|
72 |
104 |
176 |
2.2580 |
стаб. |
|
|
72 |
105 |
177 |
2.2423 |
стаб. |
|
|
72 |
106 |
178 |
2.0797 |
стаб. |
|
|
72 |
107 |
179 |
1.8040 |
стаб. |
|
|
72 |
108 |
180 |
1.2806 |
стаб. |
|
|
72 |
109 |
181 |
1.1530 |
42.39
дн |
β- (100) |
|
72 |
110 |
182 |
1.2140 |
8.9·106 л |
β- (100) |
|
72 |
111 |
183 |
0.6850 |
1.07 ч |
β- (100) |
|
72 |
112 |
184 |
0.4750 |
4.12 ч |
β- (100) |
| 72 |
113 |
185 |
0.0150 |
3.5 мин |
β- (100) |
Изотопы Hf c A = 176–180 являются стабильными
изотопами. Эти изотопы также имеют положительную энергию α‑распада. Однако энергия
α-распада ~1.3–2.2 МэВ
слишком мала и α‑распад
этих изотопов не обнаружен, несмотря на отличную от нуля вероятность α-распада. При
дальнейшем увеличении массового числа A > 180 доминирующим каналом распада становится
β--распад.
При радиоактивных распадах
конечное ядро может оказаться не только в основном, но и в одном из возбужденных
состояний. Однако сильная зависимость вероятности α-распада от энергии α‑частицы приводит к тому, что
распады на возбужденные уровни конечного ядра обычно идут с очень низкой
интенсивностью, потому что при возбуждении конечного ядра уменьшается энергия
α‑частицы. Поэтому
экспериментально удается наблюдать только распады на вращательные уровни,
имеющие относительно низкие энергии возбуждения. Распады на возбужденные уровни
конечного ядра приводят к возникновению тонкой структуры энергетического спектра
вылетающих α‑частиц.
Основным фактором, определяющим
свойства α-распада,
является прохождение α‑частиц через потенциальный барьер. Другие факторы проявляются
сравнительно слабо, но в отдельных случаях дают возможность получить
дополнительную информацию о структуре ядра и механизме α‑распада ядра. Одним из таких факторов
является появление квантовомеханического центробежного барьера. Если α‑частица вылетает из
ядра (A,Z),
имеющего спин Ji,
и при этом образуется конечное ядро
(A-4, Z-2) в состоянии со спином Jf, то
α‑частица должна унести
полный момент J, определяемый соотношением
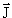 i
= i
= 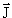 f
+ f
+ 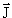 . .
Так как α-частица имеет нулевой спин, её полный
момент J совпадает
с уносимым α-частицей
орбитальным моментом количества движения l
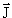 = =
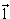 . .
В результате возникает квантовомеханический центробежный барьер.
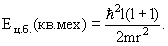 |
(2.7) |
Точно так же, как в случае потенциального барьера,
α-частица может пройти
через центробежный барьер за счёт квантовомеханического туннелирования. Высота
центробежного барьера, как правило, значительно ниже высоты кулоновского потенциального
барьера. Однако, добавляясь к Vкул , он увеличивает результирующий барьер,
через который туннелирует α-частица
Изменение формы потенциального
барьера за счет центробежной энергии незначительно главным образом из-за того,
что центробежная энергия спадает с расстоянием значительно быстрее кулоновской
(как 1/r2, а не как 1/r). Однако, поскольку это
изменение делится на постоянную Планка и попадает в показатель экспоненты, то
при больших
l, оно
приводит к изменению времени жизни ядра.
В таблице 2.2 приведена
рассчитанная проницаемость центробежного барьера Bl для α-частиц, вылетающих с орбитальным моментом
l относительно
проницаемости центробежного барьера B0 для α-частиц, вылетающих с орбитальным моментом
l = 0 для ядра с Z = 90, энергия α-частицы Eα = 4.5 МэВ. Видно, что с
увеличением орбитального момента l, уносимого α-частицей, проницаемость
квантовомеханического центробежного барьера резко падает.
Таблица 2.2
Относительная проницаемость
центробежного барьера для α-частиц,
вылетающих с орбитальным
моментом l
(Z = 90, Eα = 4.5 МэВ)
| Орбитальный момент l |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| Bl/B0 |
1 |
0.84 |
0.60 |
0.36 |
0.18 |
0.078 |
0.028 |
Более существенным фактором,
способным резко перераспределить вероятности различных ветвей α-распада, может оказаться
необходимость значительной перестройки внутренней структуры ядра при испускании
α‑частицы.
Если начальное ядро сферическое, а основное состояние конечного ядра сильно
деформировано, то для того чтобы эволюционировать в основное состояние конечного
ядра, исходное ядро в процессе испускания α‑частицы должно перестроиться,
сильно изменив свою форму. В подобном изменении формы ядра обычно участвует
большое число нуклонов и такая малонуклонная система, как α‑частица, покидая ядро, может
оказаться не в состоянии его обеспечить. Это означает, что вероятность
образования конечного ядра в основном состоянии будет незначительной. Если же
среди возбужденных состояний конечного ядра окажется состояние близкое к
сферическому, то начальное ядро может без существенной перестройки перейти в
него в результате α‑распада
Вероятность заселения такого уровня может оказаться большой, значительно
превышающей вероятность заселения более низколежащих состояний, включая
основное.
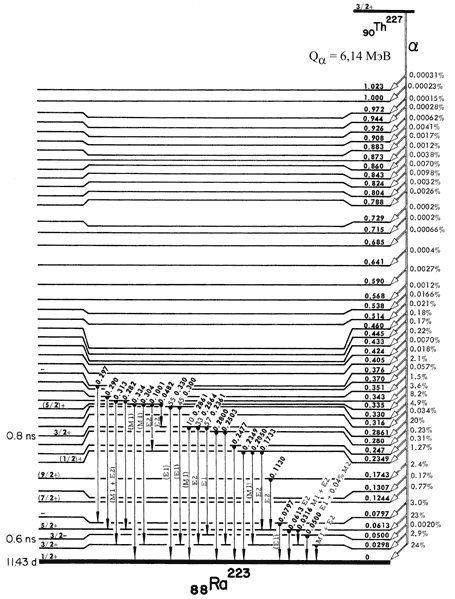
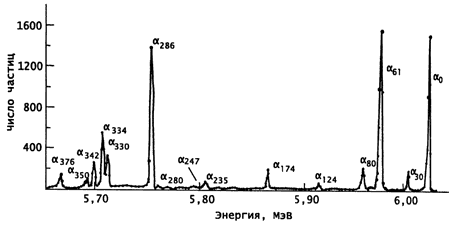
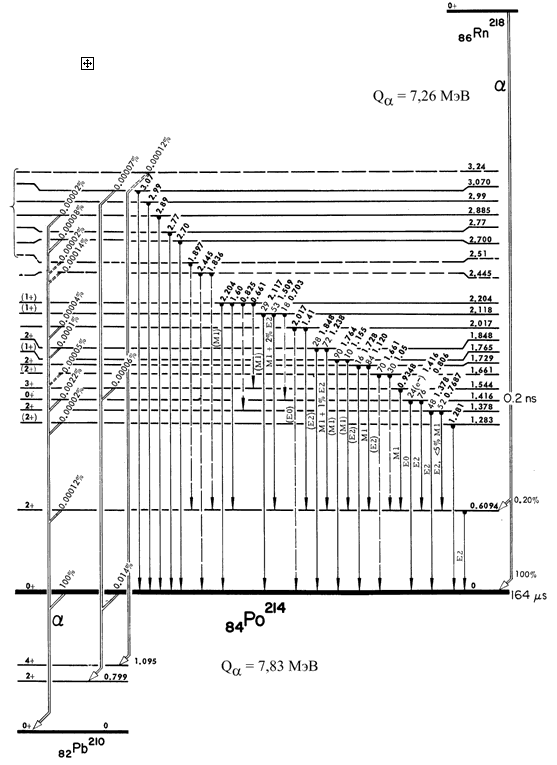
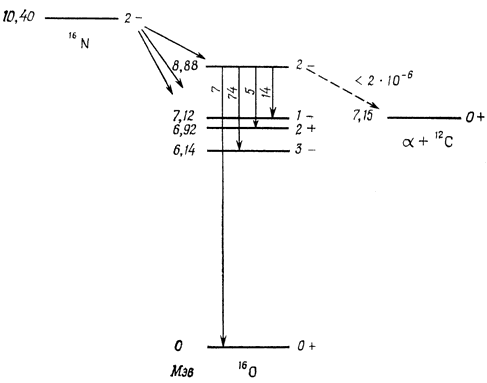
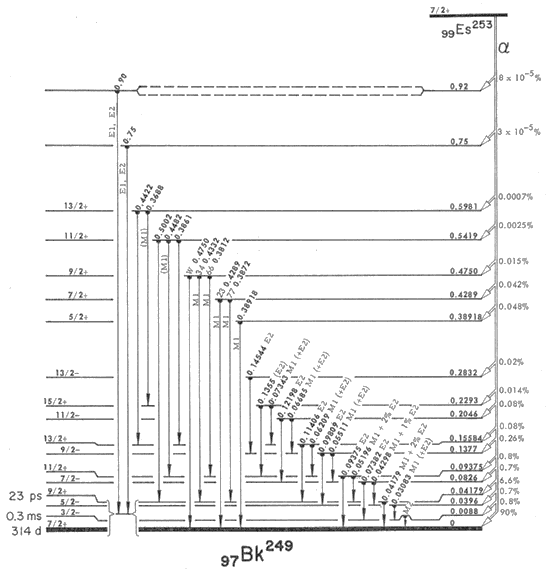
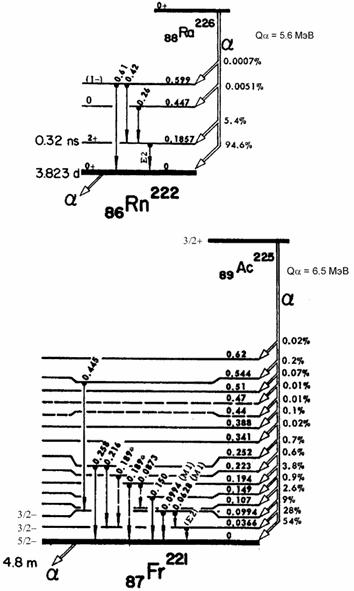
Из диаграмм α-распада изотопов 253Es,
225Ac, 225Th, 226Ra
видны сильные зависимости вероятности α-распада на возбужденные состояния от
энергии α-частицы
и от орбитального момента l, уносимого α-частицей.
α-распад также может происходить из
возбужденных состояний атомных ядер. В качестве примера в таблицах 2.3, 2.4
приведены моды распада основного и изомерного состояний изотопов 151Ho и
149Tb.
Таблица 2.3
α-распады основного и изомерного состояний 151Ho
| 151Ho |
Энергия, кэВ |
Спин четность JP |
Период
полураспада |
Каналы
распада, % |
| Основное состояние |
0.0 |
(11/2)– |
35.2 c |
e, 78;
α, 22 |
| Изомерное состояние |
0.40 |
(1/2)+ |
47.2
c |
α, 80;
e, 20 |
Таблица 2.4
α-распады основного и изомерного состояний 149Tb
| 149Tb |
Энергия, кэВ |
Спин четность JP |
Период
полураспада |
Каналы
распада, % |
| Основное состояние |
0.0 |
(1/2)+ |
4.2 ч |
e, 83.3;
α,
16.7 |
| Изомерное состояние |
35.8 |
(11/2)– |
4.2 мин |
α, 99.98;
e, 0.02 |
На рис. 2.6 приведены
энергетические диаграммы распада основного и изомерного состояний изотопов 149Tb и
151Ho.
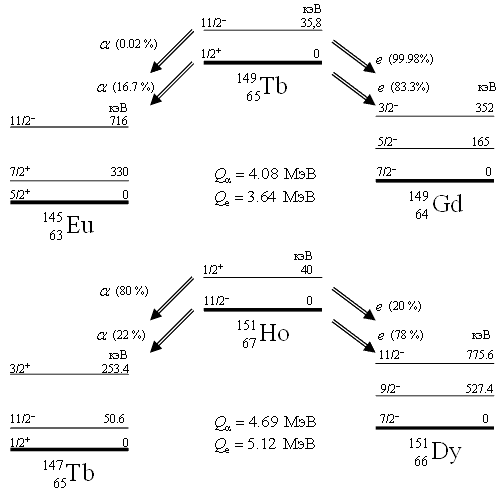
Рис. 2.6 Энергетические диаграммы распада основного и
изомерного состояний изотопов 149Tb и 151Ho.
α-распад из изомерного состояния изотопа 151Ho (JP
= (1/2)+, Eизомер =
40 кэВ) более вероятен (80%), чем е-захват
на это изомерное состояние. В то же время основное состояние 151Но
распадается преимущественно в результате е-захвата (78%).
В изотопе 149Tb распад
изомерного состояния (JP = (11/2)-, Eизомер =
35.8 кэВ) происходит в подавляющем случае в
результате е-захвата. Наблюдаемые особенности распада основного и изомерного
состояний объясняются величиной энергии α-распада и е-захвата и орбитальными
моментами, уносимыми α-частицей или нейтрино. |



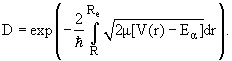

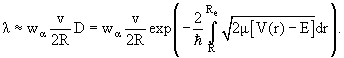



 .
.
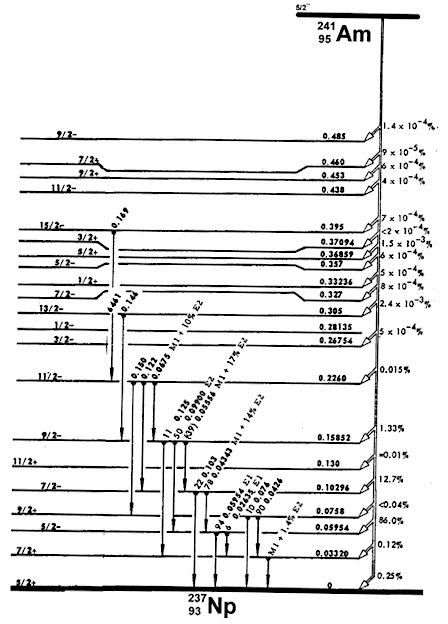
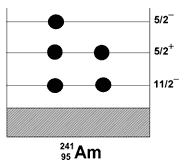 Изотоп
241Am является деформированным нечетно-четным
ядром (Z = 85, N = 146). По два спаренных протона заполняют
одночастичные состояния JP = 11/2-, 5/2+ и один неспаренный протон находится в
состоянии
Изотоп
241Am является деформированным нечетно-четным
ядром (Z = 85, N = 146). По два спаренных протона заполняют
одночастичные состояния JP = 11/2-, 5/2+ и один неспаренный протон находится в
состоянии