I. Общие принципы построения квантовой теории поля (КТП) (одна лекция).

Тема №1:

• Стандартные обозначения, верхние и нижние индексы.
•  Система единиц ћ = с = 1.
• Система единиц Хевисайда (α_em = е²/4π).
• Закон Кулона и уравнения Максвелла в новой системе единиц.
• Ограничения, накладываемые на измеряемые величины соотношением неопределенности при конечной скорости света.
• Основное отличие КТП от КМ: возможность рождения и уничтожения частиц.
• Чем характеризуются элементарные частицы в эксперименте?
• Типичная постановка задачи в КТП: сечения рассеяния и ширины распадов. Примеры некоторых интуитивно ясных диаграмм Фейнмана.

II. Основы лагранжева формализма в КТП (одна лекция).

Тема №2:

• Принцип наименьшего действия. Лагранжиан и плотность лагранжиана
• Уравнения Лагранжа.
• Гамильтониан, импульс, момент количества движения.
• Пример лагранжева подхода для уравнений Максвелла.
• Тензор напряженности электромагнитного поля.

III. Электромагнитное поле (две лекции).

Тема №3:

• Решение уравнений Максвелла для свободного электромагнитного поля в калибровке Лоренца.
• Энергия и импульс классического электромагнитного поля.
• Задача о гармоническом осцилляторе в пространстве Фока.
• Квантование электромагнитного поля как набора гармонических осцилляторов.
• Операторы рождения и уничтожения. Коммутационные соотношения между операторами рождения и уничтожения.
• 4-потенциал, энергия и импульс квантованного электромагнитного поля.
• Калибровка Лоренца для квантованного электромагнитного поля. Решение проблемы скалярных и продольных фотонов.

Тема №4:

• Калибровочные преобразования и вектора поляризации.
• Суммирование по поляризациям. Матрица плотности фотонов.
• Коммутационные соотношения для операторов электромагнитного поля. Перестановочная функция электромагнитного поля.
• Вакуумные средние и функции .
• Определения нормального и хронологического произведений. Свертка операторов электромагнитного поля.
• Связь свертки с вакуумным средним и причинной функцией Грина . Введение термина "пропагатор".
• Правила обхода полюсов в пропагаторе виртуального фотона

IV. Дираковское поле (семь лекций).

Тема №5:

• Что говорит эксперимент о частицах и античастицах?
• Уравнение Паули. Алгебра матриц Паули.
• Уравнение Клейна - Гордона - Фока.
• Вывод уравнения Дирака для свободного фермиона в несимметричной форме. Естественное возникновение биспиноров.
• Симметричная форма уравнения Дирака. Явный вид γ-матриц в стандартном представлении (представлении Паули-Дирака). Спиральное и спинорное представления.
• Решение уравнения Дирака для свободной частицы с положительной энергией u(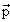,λ) в стандартном представлении. Нормировка решения.

Тема №6:

• Алгебра матриц Дирака,
  • Свойства матриц γ⁵ и σ^μν.
  • Вычисление следов от произведений матриц Дирака.
  • Разложение произведений матриц Дирака по базису.
  • Свертки по индексам и другие полезные формулы.

Тема №7:

• Введение внешнего поля в уравнение Дирака (р_μ → р_μ − еА_μ, где е = −|е|).
• Уравнение Дирака для античастицы (е → −е).
• Операция зарядового сопряжения дираковского поля.
• Явный вид оператора зарядового сопряжения в стандартном представлении (С = iγ²γ⁰) и его свойства.
• Решение уравнения Дирака для свободной античастицы в стандартном представлении v(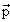,λ). Нормировка решения.
• Релятивистское обобщение оператора спина 1/2 и проекционного оператора.
• Преобразование Фолди - Вутхайзена.
• Определение спиральности.
• Соотношение v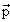(ε, , λ) = u(−ε, −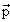, −λ) в плоскости комплексной энергии ε.

Тема №8:

• Матрица плотности для свободного решения уравнения Дирака.
• Лагранжиан свободного дираковского поля.
• Введение взаимодействия с электромагнитным полем.
• Энергия, импульс и заряд свободного дираковского поля.
• Квантование свободного решения. Принцип Паули. Коммутационные соотношения для операторов рождения и уничтожения.
• Вакуумные средние произведения операторов дираковского поля.
• Определение нормального и хронологического произведений операторов дираковского поля
• Свертка операторов дираковского поля. Связь свертки с вакуумным средним и функцией Грина.
• Пропагатор дираковского поля и правило обхода полюсов.

Тема №9:

• Полный лагранжиан КЭД.
• Глобальные калибровочные преобразования. Сохранение заряда.
• Локальные калибровочные преобразования. Фиксация вида взаимодействия.
• Зарядовая четность фотона и теорема Фарри.
• СРТ - теорема па примере КЭД. Экспериментальная проверка СРТ-теоремы.

V. S-матрица и правила Фейнмана (три лекции).

Тема №10:

• Гамильтониан взаимодействия в КЭД
• Представления Шредингера и Гейзенберга.
• Представление взаимодействия. Особая роль представления взаимодействия в квантовых теориях поля.
• Матрица рассеяния (S-матрица) и се запись в виде ряда.
• Теорема Вика (без доказательства).

Тема №11:

• Вывод правил Фейнмана для КЭД па примере вычисления матричных элементов первого порядка теории возмущений (нефизические).
• Продолжение вывода правил Фейнмана для КЭД на примере вычисления матричных элементов процессов второго порядка теории возмущений.
• Правила Фейнмана для вычисления петлевых диаграмм (без вывода).

VI. Сечения, ширины распадов и кинематика.

Тема №12:

• Выражение для вероятности перехода i → ƒ в единицу времени через <ƒ |S⁽ⁿ⁾| i>.
• Плотность конечных состояний и фазовый объем.
• Выражение для ширины распадов.
• Выражение для сечения реакции 2 → n.
• Выражение для сечения реакции 2 → 2.
• Мандельстамовские переменные.
• Кросс-каналы и физические области.

VII. Вычисление процессов в КЭД (семь лекций).

Тема №13:

• Вычисления для эффекта Комптона е⁻γ → е⁻γ
• Рассеяние электрона на ядре.

Тема №14:

• Сечение реакции аннигиляции электрон-позитронной пары в мюоны: е⁺е⁻ → μ⁺μ⁻.
• Сечение е⁺е⁻-аннигиляции в адроны и заряды кварков.
• Поля массивных векторных частиц.
• Пропагатор нестабильной векторной частицы.

Тема №15:

• Сечение е⁺е⁻-аннигиляции в адроны вблизи резонансов и формула Брейта-Вигнера.

Тема №16:

• Поля заряженных скалярных мезонов.
• Рассеяние электрона на пионе е⁻π⁻ → е⁻π⁻.
• Электромагнитный формфактор заряженного пиона F_π(q²).
• Эффект Комптона на пионе: π⁻γ → π⁻γ.
• Процессы во внешнем поле. Рассеяние е⁻ в кулоновском поле ядра.
• Излучение мягких фотонов. Инфракрасная катастрофа.

Д.1. Решение Волкова для уравнения Дирака.

Д.II. Элементы квантовой хромодинамики (КХД).

• Обоснования квантовой хромодинамики
• Лагранжиан квантовой хромодинамики
  • Полный лагранжиан КХД
  • Построение полного лагранжиана КХД
• Алгебра матриц Гелл-Манна
  • Число и явный вид матриц Гелл-Манна
  • Фундаментальное представление группы SU(2)
  • Группа SU(N)
• Рассеяние кварка одного сорта на кварке другого сорта и аннигиляция кварков
• Правила Фейнмана для трехглюонной вершины
• Реакция превращения глюонов в кварк - антикварковую пару
• Правила Фейнмана для четырехглюонной вершины

Задачи