2 Множественность частиц и плотность энергии
Множественность частиц является самой первой и наиболее
просто измеряемой характеристикой в эксперименте. По ее свойствам уже можно
сделать важные заключения. Данные экспериментов при различных энергиях для
поперечной энергии заряженных частиц хорошо аппроксимируются степенной
зависимостью от энергии (рис. 1).

Рис. 1: Измеренная поперечная энергия на единицу быстроты при η = 0 и
бьёркеновская плотность энергии рожденного сгустка материи при τ0 = 1
Фм/с (правая шкала) в центральных столкновениях тяжелых ионов [19, 20].
Экстраполяция для LHC соответствует степенному закону зависимости от энергии.
На этом рисунке приведена также оценка плотности энергии в
образованном сгустке материи в предположении поперечного расширения при средних
значениях псевдобыстрот (Определения кинематических переменных даны в приложении
9.2.) по формуле Бьёркена [14]
 |
(1) |
В этом случае для радиуса ядра R = 6.5 Фм и времени термализации τ0 ~ 1 Фм/с
протяженный объем цилиндра равен V = πRA2τ0 ≈ 150 Фм3.
Значения плотности энергии εBj ~ 5 ГэВ/Фм3 и εBj ~ 10 ГэВ/Фм3 для RHIC и LHC
соответственно. Уже при энергиях RHIC значение εBj превышает критическую
плотность энергии ~ 1 ГэВ/Фм , полученную в расчетах КХД на решетках и
необходимую для деконфайнмента.
Формулу Бьёркена можно использовать для оценки верхней границы времени
термализации, т.к. она связывает плотность частиц n0 =
dN/dη(η = 0)/(cπRA2) и время
начала остывания сгустка материи:
 |
(2) |
Если воспользоваться формулами гидродинамики для безмассовых партонов [15],
то плотность частиц однозначно связана с температурой
 |
(3) |
При критической температуре Tс = 192 МэВ, полученной из расчетов на решетке,
и факторе g: равном 40 для u-, d -кварков и глюонов, получим n = 3.75 Фм-3 , т.е. термализованный сгусток должен образоваться при t < 2.7 Фм/c.
В e+e− → q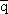 → X, где партоны изначально рождаются пертурбативно с
высокой виртуальностью, многие характеристики продольного и поперечного
распределения множественности могут быть поняты количественно из динамики пертурбативного партонного
ливня, несмотря на неопределенности процесса фрагментации. И наоборот, в
адронных столкновениях распределения по множественности включают в себя
непертурбативные процессы с малыми поперечными импульсами. Понимание адронных
процессов из первых принципов отсутствует. Даже для протон-протонных
столкновений экстраполяция множественности заряженных частиц dNch/dy от
Теватрона (√s =1.8 ТэВ) к LHC (√s = 14 ТэВ) приводит к результатам,
отличающимся на фактор 2 для моделей, описывающих данные при энергиях Теватрона
[16]. Для ядро-ядерных столкновений предсказания множественности для
минимум-биас событий (событий без искажения способом регистрации) отличаются
между собой на порядок величины. → X, где партоны изначально рождаются пертурбативно с
высокой виртуальностью, многие характеристики продольного и поперечного
распределения множественности могут быть поняты количественно из динамики пертурбативного партонного
ливня, несмотря на неопределенности процесса фрагментации. И наоборот, в
адронных столкновениях распределения по множественности включают в себя
непертурбативные процессы с малыми поперечными импульсами. Понимание адронных
процессов из первых принципов отсутствует. Даже для протон-протонных
столкновений экстраполяция множественности заряженных частиц dNch/dy от
Теватрона (√s =1.8 ТэВ) к LHC (√s = 14 ТэВ) приводит к результатам,
отличающимся на фактор 2 для моделей, описывающих данные при энергиях Теватрона
[16]. Для ядро-ядерных столкновений предсказания множественности для
минимум-биас событий (событий без искажения способом регистрации) отличаются
между собой на порядок величины.
Тем не менее, в адронных столкновениях имеется несколько характеристик,
сохраняющихся при изменении энергии √s на несколько порядков:
1. Протяженный продольный скейлинг.
Распределение по псевдобыстроте частиц ложится на универсальную и не
зависящую от энергии кривую в области фрагментации налетающей частицы.
Продольный скейлинг − сохранение зависимости от быстроты при сдвиге на величину
быстроты частицы пучка η ' = η − ybeam [17]. Область, где остается та же
зависимость, увеличивается с энергией (см. рис. 2). Если тенденция предельной
фрагментации сохранится, то это войдет в противоречие с Лоренц-инвариантным
плато по продольному импульсу в области средних быстрот, предсказываемым
бьёркеновским скейлингом.
Плато на рис. 2 при энергиях RHIC дает величину множественности
 /dη(0)
= 675, а при энергии LHC для РbРb-столкновений − /dη(0)
= 675, а при энергии LHC для РbРb-столкновений −
 /dη(0)
~ 1100. /dη(0)
~ 1100.
2. Факторизация зависимостей
от энергии √s и от центральности
столкновения.

Рис. 2: Множественность заряженных частиц как функция псевдобыстроты η ' = η − ybeam
в AuAu-столкновениях при различных энергиях в системе центра масс от √s =
19.6 ГэВ до √s = 5.5 ТэВ. Данные приведены в системе покоя одного из
сталкивающихся ядер с зеркальным отражением для другого ядра [21, 22].
Экстраполяция для LHC приведена в двух вариантах: 1) продолжение предельной
фрагментации и 2) трапецеидальная форма.
Для всех процессов нормированное распределение по множественности (в терминах
числа участвующих нуклонов Npart двух сталкивающихся ядер)
(Определения и способ вычисления смотрите в приложении 9.3.) есть одно и то же
базисное распределение, не зависящее от энергии (см. рис. 3).
Сохранение продольного скейлинга означает, что dN/dy будет расти почти
логарифмически с ростом энергии ~ (а + by) ~ (а +
b ln(Е/mT)) . Однако модели,
основанные на пертурбативном механизме рождения частиц при высоких энергиях,
предсказывают более сильную степенную зависимость от энергии, не подтверждаемую
данными RHIC. Это один из главных факторов, инициировавших исследование так
называемых моделей партонного насыщения. Подавление сильного роста
множественности связано с нелинейной зависимостью партонной эволюции от
плотности партонов. При высоких энергиях возрастает роль партонных распределений
при малых
х ~ 1/√s: увеличивающих вклад жесткой компоненты рождения частиц. С
этим связано увеличение dN/dy с ростом Npart. Насыщение плотности партонов при
малых х приводит к ослаблению степенного роста с энергией. Модели насыщения
предсказывают, что множественность растет пропорционально квадрату импульса
насыщения Q2sat А, зависящего от энергии и от A . В этом случае получена
простая формула [18]
 |
(4) |
Здесь N0 = 0.47 берется из фита данных RHIC, параметры λ = 0.228 и δ = 0.8 −
из данных неупругого еA-рассеяния. Эта формула реализует свойство факторизации
(пункт 1) и описывает зависимости от энергии (рис. 1) и от центральности
столкновения (рис. 3). Для энергий LHC она дает значение
 /dη(0) ~ 1650,
что соответствует максимуму пунктирной кривой на рис. 2. /dη(0) ~ 1650,
что соответствует максимуму пунктирной кривой на рис. 2.
Обсуждая множественность частиц, следует также остановиться на зависимости от
поперечного импульса. На рис. 4 представлены спектры для пионов, каонов и
протонов (антипротонов) до
pT < 5 ГэВ/c. В сравнении с pp-столкновениями параметр
обратного наклона кривых больше и увеличивается с ростом адронной массы и
центральности столкновения, как и ожидается для коллективного расширения сгустка
в модели взрывной волны [3]. Спектры хорошо описываются гидродинамическими
расчетами, учитывающими партоннную фазу при малых временах образования
термализованного вещества (τ < 1 Фм/c).

Рис. 3: Зависимость множественности частиц от центральности столкновений и от
энергии величины dNch/dη(0), нормированной на число пар участвующих нуклонов Npart/2 (данные PHOBOS [1]). Затененные области — предсказания модели насыщения
[18].

Рис. 4: Данные RHIC для спектров по поперечному импульсу пионов, каонов и
(анти)протонов в центральных 0-10% AuAu-столкновениях в сравнении с
комбинированным расчетом в гидродинамической модели и пертурбативной КХД [23].
Для наглядности кривые сдвинуты на фактор, указанный на врезке.
Иллюстрации к данному разделу
(слайды 2-8).
  

|





