2.3. Ионизационные потери электронов
Вывод формулы для потерь энергии на ионизацию электронами в принципе такой же, как и для других заряженных частиц. Также для электронов (z = 1) получается соотношение:

но величины bmax и bmin приходится выбирать несколько по-другому. Необходимо при этом учитывать, что
1) падающие электроны в процессе взаимодействия из-за малости своей массы будут отклоняться от первоначального направления;
2) из-за тождественности взаимодействующих частиц будут возникать обменные эффекты, имеющие квантовую природу.
При учете этих замечаний формула для удельных ионизационных потерь принимает вид:

В этой формуле
 − релятивистская кинетическая энергия электрона. − релятивистская кинетическая энергия электрона.
В нерелятивистском случае формула сводится к более простому выражению:

В ультрарелятивистском случае при E >> mec2 формула для
потерь энергии также имеет простой вид:

В отличие от тяжелых частиц для электронов важны оба эти предельных случая, так как
mec2 = 0.511 МэВ и электрон становится ультрарелятивистским уже при энергии в несколько МэВ.
Сравнение ионизационных потерь для электронов и тяжелых заряженных частиц приводит к следующим выводам.
- Множители перед квадратными скобками в выражениях для ионизационных потерь электронов и тяжелых заряженных частиц одинаковы, т.е. при одинаковых скоростях удельные потери их одинаковы.
- При одной и той же энергии электронов и тяжелых частиц в нерелятивистском случае удельные потери энергии пропорциональны массе частиц. Следовательно, для протонов они почти в 2000 раз больше, чем для электронов. Это очень важно для методов регистрации частиц. Например, в ядерных эмульсиях протоны с энергией 5 МэВ оставляют отчетливый след, тогда как электрон такой же энергии практически незаметен.
- При очень высоких энергиях все по-другому. При V ~ c член перед скобкой не меняется. Становится существенной зависимость от √1 − β2 под логарифмом. Поэтому при ультрарелятивистских скоростях величина dE/dx слабо зависит и от энергии, и от массы частицы. Например, при кинетической энергии электрона и протона,
равных 10 ГэВ потери энергии электронами в ≈ 2 раза превышают
потери энергии протонами (при различии их масс в 2000 раз).
2.4. Пробег заряженных частиц в веществе
Потеряв всю энергию, частица останавливается. Расстояние, пройденное частицей в веществе, называется пробегом. На этом пути заряженная частица изменяет свою энергию от начального значения E0 до нуля в результате разных механизмов взаимодействия, основным из которых для области энергий до 100 МэВ являются ионизационные потери. Поэтому понятно, что величина пробега зависит от массы,
заряда, энергии частиц и характеристик среды.
Пробег R частицы с начальной энергией Е0 можно определить выражением

Для нерелятивистских частиц dE = d(MV2/2) = MVdV, а

Оценим теперь, как пробег зависит от параметров частицы и
среды:

Из этого соотношения можно сделать ряд полезных выводов:
- При равных скоростях пробеги частиц прямо пропорциональны их
массам и обратно пропорциональны квадратам зарядов.
Пробеги обратно пропорциональны плотности среды, т.е. удобно измерять пробеги в массовых единицах длины. В этом случае величина пробега практически не будет зависеть от характеристик среды:
Rρ (г/см2) ~ MV4/z2.
При более аккуратных расчетах не следует забывать, что в формуле Бете-Блоха есть еще коэффициенты, зависящие от среды: Z/A и I. Но для большинства веществ с малыми и средними A величина отношения Z/A ~ 0.5 и очень медленно падает с увеличением A, а средний ионизационный потенциал I стоит под знаком логарифма, т.е. тоже слабо влияет на величину средних потерь энергии и, как следствие этого, на величину пробега.
Чтобы сравнивать пробеги частиц с одинаковыми кинетическими
энергиями, удобно несколько преобразовать выражение для R:

Из этот соотношения видно, что при равных кинетических
энергиях пробеги частиц обрагно пропорциональны их массам.
Пусть на слой поглотителя перпендикулярно к нему падает пучок однородных частиц с одинаковой энергией E0. Как будет выглядеть зависимость числа этих частиц N от толщины поглотителя x?
Для тяжелых заряженных частиц (практически всех частиц, кроме электронов), которые проходят слой поглотителя почти без рассеяния и поэтому имеют прямолинейную траекторию в веществе, все очень просто: частицы выбывают из пучка в основном из-за остановки в результате потерь энергии на ионизацию и возбуждение среды. А так как у них начальная энергия E0 была одинакова и средние потери энергии dE/dx тоже одинаковы, то все частицы должны были бы проходить одинаковые расстояния в веществе. В этом случае кривая поглощения должна описываться горизонтальной резко обрывающейся линией. На самом деле, вместо этой картины наблюдается статистическим характером процесса ионизационных потерь. Частицы теряют свою энергию в очень большом, но конечном числе отдельных
актов. Флукгуациям подвержено как число таких актов на единицу длины, так и
потери энергии в каждом отдельном акте, в особенности в связи с образованием δ-элекгронов.
Пробеги отдельных частиц распределены около среднего пробега
по закону Гаусса:

где R средний пробег,
 − среднеквадратичное отклонение от среднего значения. − среднеквадратичное отклонение от среднего значения.
Относительный разброс пробегов
 называется стрэгглингом. Наличие этого разброса приводит к тому, что кривая поглощения имеет не резкий, а плавный спад, такой, как изображен на рис. 2.6 а (для α-частиц). На основании свойств гауссова распределения можно найти, что интенсивность пучка упадет в два раза в точке x = R0, которая соответствует среднему пробегу частиц. Более того, в этой точке кривая имеет наибольшую крутизну. Построив касательную с максимальным наклоном в точке x = R0 и продолжив ее до пересечения с осью абсцисс, можно найти экстраполированный пробег Rэ. Обычно разность
Rэ – R0 называется параметром разброса. Величина параметра разброса для тяжелых заряженных частиц незначительна и составляет единицы или десятые доли процента от R0. Это обстоятельство дает возможность по величине пробега с хорошей точностью определять энергию частиц. называется стрэгглингом. Наличие этого разброса приводит к тому, что кривая поглощения имеет не резкий, а плавный спад, такой, как изображен на рис. 2.6 а (для α-частиц). На основании свойств гауссова распределения можно найти, что интенсивность пучка упадет в два раза в точке x = R0, которая соответствует среднему пробегу частиц. Более того, в этой точке кривая имеет наибольшую крутизну. Построив касательную с максимальным наклоном в точке x = R0 и продолжив ее до пересечения с осью абсцисс, можно найти экстраполированный пробег Rэ. Обычно разность
Rэ – R0 называется параметром разброса. Величина параметра разброса для тяжелых заряженных частиц незначительна и составляет единицы или десятые доли процента от R0. Это обстоятельство дает возможность по величине пробега с хорошей точностью определять энергию частиц.

Рис.2.6. Зависимость числа
частиц от толщины поглотителя: а
– альфа-частиц,
б
– электронов
Для электронов ситуация с пробегами иная. Понятие пробега для электронов весьма условно, потому что кроме ионизационных потерь для электронов существенную роль играют радиационные потери энергии. Кроме того, электроны испытывают в веществе многократное рассеяние, и поэтому их путь в веществе не прямолинеен (как для тяжелых частиц). Направление их движения часто меняется, и только небольшое число электронов из пучка проходят максимальное расстояние в поглотителе в направлении, перпендикулярном к его поверхности. Кривая поглощения коллимированного пучка моноэнергетических электронов имеет другой, чем для тяжелых частиц, вид (рис.2.6 б).
Относительный разброс пробегов (стрэгглинг) и параметр разброса для электронов значительно больше, чем для других частиц. Для электронов вводят еще одно понятие: максимальный пробег Rmax, это толщина вещества, в которой задерживаются все электроны. Теоретически рассчитать Rmax очень трудно. Поэтому для оценок обычно пользуются полуэмпирическими формулами. Например, для моноэнергетических электронов с энергией E (МэВ) часто применяется простая формула:
Rmax (г/см2) = 0.526E (МэВ) − 0.24.
Обычно энергию электронов определяют не по пробегу, а по полной ионизации, произведенной ими в веществе.
2.5. δ-электроны
При столкновении заряженной частицы с электроном среды в случае достаточно малого параметра удара b ~ a электрон может получить такую энергию, что сам будет вызывать ионизацию других атомов. Такие электроны называются δ-электронами.
При ионизационных потерях в каждом столкновении пролетающей частицы с электроном среды в среднем ею теряется очень небольшая порция энергии. И только в редких случаях передается значительная энергия, т.е. образуется δ-электрон. Вспомним уже полученное нами соотношение между энергией электрона Те и параметром удара:
Te = 2z2e4/meV2b2.
Отсюда следует заключение, что большая передача энергии с образованием δ-электрона осуществляется при малых параметрах удара. Поэтому вероятность образования δ-электронов определяется вероятностью оказаться электрону среды в кольце площадью 2πbdb около траектории частицы, т.е.
dσδ = 2πbdb. Но

Следовательно,

При прохождении частицей пути dx она передает энергию Тe каждому из электронов среды, находящихся в объеме кольцевого цилиндра радиуса b, с площадью кольца 2πbdb и длиной dx. Объем такого кольцевого цилиндра −
2πbdbdx, а количество электронов, находящихся в нем − ne·2πbdbdx, где ne
− плотность электронов в среде. Таким образом, на единице своего пути в веществе частица образует следующее число δ-электронов с энергией в интервале (Te, Te + dTe):
dNδ = 2πbdbdx·ne = nedxdσδ.
Подставляя выражение для dσδ получим:

где

Таким образом, мы получили энергетический спектр δ-электронов
dNδ/dTe = Q/Te2,
из которого видно, что наиболее часто образуются δ-электроны малых энергий и по мере увеличения энергии δ-электронов число их резко падает.
Для релятивистских частиц β ≈ 1 величина Q перестает зависеть от энергии частицы:

а число δ-электронов с энергией Тe(МэВ) в интервале (Te,Te + dTe), созданных в среде на пути в 1 г/см2 релятивистской частицей, получается равным:

Из этой формулы видно, что число δ-электронов с энергией Тe, образованных в 1 г/см2 вещества релятивистской частицей, прямо пропорционально квадрату заряда частицы z2 и практически не зависит от характеристик среды, так как Z/A ≈ 0,5. Отсюда следует, что по плотности δ-электронов на треке частицы (например, в пузырьковой или фотоэмульсионной камере) можно определить заряд z релятивистской частицы.
Чтобы найти число δ-электронов на единице пути частицы (плотность δ-электронов), надо проинтегрировать по всем возможным энергиям δ-электронов Те от минимальной до максимальной:

Te min − некоторая нижняя граница δ-электронов, которая может быть выбрана довольно произвольно, но при условии, что δ-электроны все же могут сами ионизовать. Часто, например, принимают величину минимальной энергии Te min = 4·I.
Максимальная энергия, которую может получить электрон при столкновении с ним частицы массы М и кинетической энергией Е, будет: Тe max = 4meM/(M
+ me)2·E, и, если М >> me, то
Т е max = (4me/M)·E. Подставляя значения Тe min и Te max в полученное выражение для dNδ/d(xρ), найдем плотность δ-электронов на 1 г/см2 своего пути:

Угловое распределение δ-электронов в системе центра инерции (с.ц.и.) определяется формулой Резерфорда:

где θ − угол рассеяния в с.ц.и , dΩ = 2π sinθ dθ и Есци − cуммарная энергия частиц в с.ц.и.:
 если М
>> me. если М
>> me.
Для перехода в лабораторную систему координат (л.с.) воспользуемся соотношением:
ψ = (π − θ)/2, где ψ − угол вылета δ-электрона по отношению к направлению движения частицы. Отсюда: sin
θ/2 = cos ψ, sin4 θ/2 = cos4
ψ, sin θ = sin 2ψ = 2 sin
ψ cos ψ, dθ = -2dψ. Элемент телесного угла в лабораторной системе координат dω =2π sin
ψ dψ.
Распределение δ-электронов по углам в л.с. принимает вид

Из полученного соотношения видно, что большая часть δ-электронов вылетает под углами, близкими к π/2 относительно направления движения частицы.
Энергия, переданная заряженной частицей δ-электрону, связана с углом его вылета соотношением:
Te = 4meM/(M + me)2·E·cos2
ψ ≈ 4me/M·E·cos2 ψ при M >> me.
Таким образом δ-электроны, вылетающие под малыми углами к траектории частицы (ψ ~ 0), имеют максимальную энергию (Te max =
(4me/M)·E), а вылетающие под углами, близкими к π/2, имеют энергии минимальные. Зная энергию δ-электрона (например, по пробегу) и угол его вылета ψ
можно оценить энергию частицы Е.
2.6. Флуктуации ионизационных потерь
Потери энергии заряженной частицей есть статистический процесс, т.к. различные столкновения, ответственные за эти потери, представляют собой независимые события. Поэтому при прохождении через определенный слой вещества ∆x частицы одного и того же сорта и одинаковой энергии
(Е0, Е0 + dE0) теряют не одно и то же количество энергии. В среднем энергия частиц уменьшается за счет ионизационных потерь на величину
ΔE =
dE/dx·Δx, где
dE/dx − средние ионизационные потери на единице пути ( формула Бете-Блоха).
Реальные ионизационные потери флуктуируют около средних по
двум причинам. Во-первых, флуктуирует число актов столкновения в данном
слое dx, и во-вторых − флуктуирует ветчина потерь энергии в каждом отдельном столкновении с электроном среды. Результатом флуктуации ионизационных потерь является возникновение энергетического разброса в пучке моноэнергетических частиц после прохождения слоя вещества ∆x. Статистические
флуктуации потерь энергии наряженной частицей с массой М >> mе
сравнительно малы. т.к. в каждом отдельном случае передача энергии мала, а число
столкновений велико.
Для электронов ионизационные лагери энергии вообще не
являются главной причиной энергетических потерь и, тем более, главной причиной,
вызывающей флуктуации этих потерь. Поэтому обычно проблему флуктуации
ионизационных потерь энергии связывают с тяжелыми заряженными частицами (мюонами.
пионами, протонами и др.).
Характер возникающего при этом энергетического распределения частиц зависит от толщины слоя ∆x.
В 1915 г. Н.Бор показал, что флуктуации ионизационных потерь в толстых поглотителях (т.е. в таких, в которых происходит усреднение многих актов столкновения и разных передач энергии электронам вещества) подчиняются закону Гаусса:

где ΔE − средние потери энергии в слое ∆x, а D = 4жe4z2ne∆x − дисперсия распределения. Распределение Гаусса симметрично, наиболее вероятные потери совпадают со средними потерями. Но на практике обычно используются тонкие поглотители.
Поскольку характер энергетического распределения частиц, проходящих cлой ∆ x, зависит от толщины этого слоя, то необходимо количественно определить понятия "толстый" и "тонкий" слой вещества.
Назовем слой поглотителя толстым, если в нем происходит много актов столкновения с максимальной передаваемой энергией: N (> Te max) >>1. Но число столкновений на пути ∆x с передачей электрону энергии Те в интервале (Тe, Тe + dТe) было уже ранее найдено:

Следовательно, число столкновений в слое ∆x с передачей энергии Te ≥ Te max будет:

Отсюда можно получить условие "толстого поглотителя"

Если с электроном сталкивается тяжелая нерелятивистская частица, то Te max = 2meV2. Отсюда получаем, что слой ∆x поглотителя толстый, если

Если же в слое ∆x произошло мало столкновений с большой передачей энергии электронам
N(>Temax) << 1, тo такой слой будем называть тонким. Этому понятие соответствует соотношение

Величину флуктуации потерь энергии в тонких слоях вещества впервые рассчитал
Л.Д. Ландау в 1944 г. Он вывел функцию распределения потерь и получил выражение для наиболее вероятных ∆Евер и средних ∆Еср потерь энергии:

где


Рис. 2.7. Флуктуации ионизационных потерь энергии (кривая Ландау) в "тонких" слоях вещества. |
Полученное распределение называется кривой Ландау и имеет вид, схематически изображенный на рис.2.7. Распределение Ландау для "тонких " поглотителей существенно несимметрично: положение максимума кривой (∆Е = ∆Евер) не совпадает со средними потерями энергии:
∆Еср = 1.4∆Евер. Ширина распределения на половине высоты близка к 4ξ. Асимметрия обусловлена сравнительно редкими близкими столкновениями, в которых образовавшимся δ-электронам передается значительная доля энергии частицы, следовательно, при этом наблюдаются большие потери энергии.
С увеличением толщины слоя вещества происходит постепенный переход от распределения Ландау к распределению Гаусса для потерь энергии.
Функция распределения Ландау оказалась довольно похожей по форме на наблюдаемые на опыте распределения, но полуширина наблюдаемого распределения больше, чем дает Ландау.
В 1950 г. О. Блунк и С. Лейзеганг уточнили решение Ландау, учтя следующий член в разложении при вычислении функции распределения.
В 1957 г. П.В. Вавилову удалось найти точное решение задачи о флуктуациях ионизационных потерь тяжелых частиц в тонких поглотителях и определить условия, при которых можно пользоваться распределениями Гаусса и Ландау:
если ξ ≤ 0.01 Тe max, то справедливо решение Ландау с уточнением Блунка-Лейзеганга;
если 0.01 Te max ≤ ξ ≤ Te max тo надо использовать решение Вавилова;
если ξ >> Te max, то справедливо распределение Гаусса.
2.7. Кулоновское взаимодействие частиц с ядрами (упругое рассеяние)
При пролете заряженной частицы через атом в непосредственной близости от ядра происходит кулоновское взаимодействие с ядром, так как прицельный параметр (b << a) настолько мал, что кулоновское поле ядра не экранируется полем атомных электронов.
Механизм кулоновского взаимодействия частиц с ядрами в общих чертах тот же, что и при ионизационном торможении. Сравним потери энергии заряженной частицей (M,ze,V) при взаимодействии с кулоновским полем ядер (mя, Ze) и атомными электронами (me,e). При этом покажем, что передача энергии ядрам за счет кулоновских сил будет невелика по сравнению с ионизационными потерями.
- Импульс, передаваемый в одном акте взаимодействия (прицельный параметр b), с кулоновским полем ядра −
ря = 2е2z·Z/(V·b), с кулоновским полем электрона − pе = 2e2z/(V·b) ,
- Энергия, теряемая частицей в одном акте взаимодействия с ядром −
 с электроном − с электроном −

- Количество столкновений на пути dx: с ядрами − na·2πbdbdx, c электронами −
na·Z·2πbdbdx,
- Энергия, передаваемая при этих столкновениях: с ядрами −
 с электронами −
с электронами −
Отношение потерь энергии на пути dx в этих случаях будет:

Таким образом, потери энергии на упругое взаимодействие с ядрами составляют около 0.03% от ионизационных потерь, т.е. дают незначительный вклад в общие ионизационные потери энергии.
Величину энергетических потерь из-за кулоновского взаимодействия частицы с ядрами среды получают интегрированием
(dE(b)/dx)|я по всем возможным прицельным параметрам: от bmin ≈ R до bmax ≈ а, при котором наблюдается полное экранирование кулоновского поля ядра атомными электронами.

Рис.2.8. Изменение траектории частицы при единичном акте взаимодействия с кулоновским полем ядра |
Несмотря на то, что кулоновское взаимодействие частиц с ядрами среды не приводит к большим потерям энергии, тем не менее, это взаимодействие существенно, так как вызывает рассеяние частиц. Дело в том, что траектория частицы, взаимодействующей с многозарядным тяжелым ядром (Ze, mя), заметно отличается от прямолинейной. В каждом акте взаимодействия частица отклоняется от своего первоначального направления на угол рассеяния θ (рис.2.8 ).
Этот угол может быть найден из условия tg θ = ∆p/p, где
p − импульс налетающей частицы, а ∆p − приращение импульса в результате взаимодействия с рассеивающим центром. Но

Из этого соотношения видно, что:
- Наиболее сильно рассеиваются легкие частицы, а тяжелые частицы рассеиваются слабее.
- Поскольку tg θ ~ 1/b, а более вероятны далекие взаимодействия (2πbdb), то, следовательно, преобладают рассеяния на малые углы. Однако, так как в реальном случае прицельный параметр ограничен размерами атома (bmax ≈ a), то очевидно, что углы рассеяния не могут принимать сколь угодно малые значения. Иными словами, из-за эффекта экранирования рассеяния на очень малые углы маловероятны.
- Чем меньше передаваемая ядру энергия, тем меньше и угол рассеяния, так как
Тя ~ b-2.
- Поскольку tg θ ~1/pV, то частицы с большей энергией рассеиваются на меньшие углы.
2.8. Многократное рассеяние
При прохождении через вещество частицы претерпевают многократное рассеяние. Если заряженная частица движется в плотной среде, то, проходя мимо различных ядер этой среды в пределах b < bmax, она будет рассеиваться каждым из них на некоторый угол θ, среднее значение которого тем больше, чем меньше масса движущейся частицы и чем меньше ее энергия. Этот процесс упругих рассеяний частицы в кулоновском поле ядер, мимо которых она движется, называется
многократным кулоновским рассеянием.
Пусть в результате N столкновений на пути x частица испытает последовательную серию отклонений θ1, θ2,… θN. Каждый из этих углов определяется конкретными условиями данного столкновения (например, значением параметра удара bi), так что вообще говоря θ1 ≠ θ2 ≠ θ3 ≠…≠ θN. Каждое из этих отклонений может быть направлено в любую сторону относительно предшествующего. Т.к. они статистически независимы и равновероятны по разным направлениям, то суммарное отклонение будет равно нулю ∑θi = 0.
Поэтому результирующий угол рассеяния не может служить мерой многократного рассеяния. Однако из-за того, что каждое рассеяние дает угол отклонения θi ≠ 0, то для количественного описания вводится среднеквадратичный угол многократного рассеяния
 . .
Ранее было получено соотношение между угловым отклонением θ и прицельным параметром b:

Так как для малых углов tg θ ≈ θ, то можно записать:

Число столкновений с параметром удара b на пути х,
приводящих к отклонению на угол θ(b), равно N(b)db = 2πnxbdb, a полное число
столкновений на пути х будет

Среднее значение θ2 на пути x в результате N столкновений можно найти следующим образом:

и

Эта формула была бы совершенно точной, если бы на расстояниях, больших bmax, заряд ядра был полностью экранирован электронами атома, и рассеяния не было совсем, а для всех расстояний, меньших bmax и больших bmin, экранирование вообще бы
отсутствовало. Но такой определенной границы в действительности не существует,
так как с увеличением расстояния от ядра экранирование возрастает постепенно.
Однако логарифмический множитель слабо зависит от величин bmax и bmin,
и поэтому можно положить, что bmin ≈ R ядра, а bmax
≈ a − радиусу атома. По порядку величины логарифмический член равен 10.
Таким образом, если скорость частицы на пути х не меняется, то среднеквадратичный угол многократного рассеяния

В классическом случае произведение pV равно удвоенной кинетической энергии
частицы. В предельно релятивистском случае Vp ≈ с·р и почти равно кинетической
энергии, поэтому при грубой оценке можно считать, что

Многократное рассеяние играет большую роль при
экспериментальном изучении частиц большой энергии. Измерение угла многократного
рассеяния в ядерной эмульсии является эффективным методом определения жергии
быстрых частиц. В других случаях как. например, при работе с вершинными
детекторами на ускорителе. необходимо учитывать многократное рассеяние,
поскольку оно искажает углы вылета вторичных частиц и затрудняет кинематический
анализ явления.
2.9. Тормозное излучение
Тормозное излучение – это электромагнитное излучение заряженной частицей, возникающее в результате ее торможения (изменения скорости) при взаимодействии с электростатическим полем атомного ядра и атомных электронов. В электродинамике доказывается, что заряженная частица, движущаяся с ускорением, обязательно излучает электромагнитные волны. Аналогичное излучение возникает при движении электронов в однородном магнитном поле. Впервые такое излучение наблюдалось в синхротроне, и поэтому получило название синхротронное излучение. Большой интерес представляет синхротронное излучение космических объектов, например, сверхновых звезд, пульсаров, квазаров, радиогалактик. Синхротронная природа излучения подтверждается особенностями спектра фотонов и их поляризации. По этим параметрам можно определить в этих объектах концентрацию и энергетический спектр релятивистских электронов, величину направление магнитных полей.
В случае же возникновения излучения при кулоновском заряженных частиц с ядрами и электронами среды
тормозным излучением и приводит к радиационным потерям энергии заряженной частицей.
Основные закономерности тормозного излучения можно понять на основе классической электродинамики.
Пусть частица с массой М, зарядом ze и скоростью V = βс движется мимо ядра с зарядом Ze и массой mя. При кулоновском рассеянии на ядре частица претерпевает отклонение и, следовательно, получает ускорение
|dV/dt| и в течение времени dt она излучает энергию, пропорциональную квадрату ускорения:

Поскольку

то излучаемая энергия будет описываться выражением

Из этого соотношения можно сделать два важных для нас заключения.
- Потери энергии на излучение обратно пропорциональны квадрату массы частицы. Это приводит к тому, что тяжелые частицы излучают значительно меньшую энергию, чем легкие. Например, мюон (Mμ = 207me) излучает энергию в ~40000 раз меньшую, чем электрон, а протон
(Mp =1836me) − в 3.4·106 раз меньше электрона. Поэтому радиационные потери энергии наибольшее значение имеют для легчайших заряженных частиц − электронов.
- Излучаемая энергия прямо пропорциональна квадрату заряда рассеивающего центра, т.е. наиболее существенны радиационные потери в тяжелых веществах, например, в свинце. Поэтому в экспериментах с космическими лучами, где мы часто имеем дело с релятивистскими электронами и со свинцом в качестве фильтра, тормозное излучение играет очень существенную роль и его обязательно надо учитывать.
В 1934 г. Бете и
Гайтлер впервые описали тормозное излучение электрона при взаимодействии его с кулоновским полем ядра с помощью квантовой электродинамики, уравнений Дирака для электрона и борновского приближения. Ими было получено выражение для вероятности излучения электроном с энергией Е при прохождении слоя вещества (Z,A,ρ) толщиной 1см фотона с энергией Е′ в интервале (Е′,
Е′+dЕ′).Для случая Е >> mес2 оно выглядит так:

где α = e2/ћc = 1/137, re = e2/mec2
– классический радиус электрона, n – число атомов в 1 см3 , Е – полная энергия налетающего электрона. Функции Ф1 и Ф2
– учитывают экранирование кулоновского поля ядра полями атомных электронов, т.е. эти функции зависят от величины прицельного параметра b и, по сути, от начальной энергии тормозящегося электрона Е. Остановимся на этом.
Вероятность излучения существенным образом зависит от эффективного расстояния электрона от ядра, т.е. от прицельного параметра b . Дело в том, что электрическое поле ядра можно считать кулоновским, если а >> b >>
Rя (а – радиус атома, Rя – радиус ядра). Если b ~ a, то начинает сказываться экранирование поля ядра атомными электронами. При b > a экранирование будет максимальным или, как его называют,
полным. Следует заметить, что случай полного экранирования реализуется наиболее часто, т.к. сечение процесса σ = 2πbdb. Остановимся на этом подробнее.
С точки зрения классического подхода изменение импульса тормозящегося электрона

С точки зрения квантового подхода изменение импульса ∆p и прицельный параметр b связаны соотношением неопределенности Гейзенберга b·∆р ~ ħ, т.е. получили то же самое соотношение:
b ~ 1/Δp.
Используя закон сохранения энергии для случая торможения электрона, можно получить выражение для передаваемого электроном импульса:

Cледовательно прицельный параметр b связан с энергией электрона Е соотношением

где
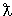 0
= ħ/mec − комптоновская длина волны электрона. Таким образом b ~ E для любого перераспределения энергии (в акте торможения) между электроном (E − E′) и фотоном (E′). 0
= ħ/mec − комптоновская длина волны электрона. Таким образом b ~ E для любого перераспределения энергии (в акте торможения) между электроном (E − E′) и фотоном (E′).
Вернемся к проблеме экранирования и определению функций Ф1 и Ф2 в формуле Бете
- Гайтлера. Чтобы учесть эффект экранирования надо сопоставить величину прицельного параметра b с размером атома а.
По модели Томаса-Ферми размер атома определяется соотношением: a =
a0Z-1/3 = 137λ0·Z-1/3, где a0 = 137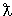 0 − боровский радиус атома водорода , а λ0 = 2.426·10-10 см − комптоновская длина волны электрона (λ0
= 2π 0 − боровский радиус атома водорода , а λ0 = 2.426·10-10 см − комптоновская длина волны электрона (λ0
= 2π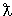 0). 0).
Если b < < a , то можно считать что взаимодействие происходит вблизи ядра, экранированием кулоновского поля ядра атомными электронами можно пренебречь. Используя приведенные выше значения b и а, можно найти энергию электрона, соответствующую этому случаю. Если положить, что Е − Е′ = Е′ (т.е. энергия делится между фотоном и электроном поровну), то соотношению b < < a cответствует соотношение 2E/mec2 << 137Z-1/3, и энергия электрона будет Е <<
(137/2)mес2 Z-1/3.
В этом случае функции Ф1 и Ф2 в формуле Бете - Гайтлера принимают вид:

Если b > a, то взаимодействие − далекое, экранирование кулоновского поля ядра максимальное (полное). Это происходит, если энергия электрона
Е > (137/2)mес2 Z-1/3.
Принято называть энергией полного экранирования величину
Eп экр =137mес2 Z-1/3.
В таблице 2.4 приведены ее значения для некоторых веществ.
Таблица 2. 4. Энергия полного экранирования
| Элемент |
Z |
A |
Eп. экр, МэВ |
| H |
1 |
1 |
68.5 |
| C |
6 |
12 |
38.5 |
| N |
7 |
14 |
36.6 |
| Fe |
26 |
56 |
23.6 |
| Pb |
82 |
207 |
15.0 |
В этом наиболее вероятном случае полного экранирования функции Ф1 и Ф2 равны:
Ф1 = ln(191Z-1/3), Ф2 = -2/3Ф1 + 1/9. Сама формула Бете -Гайтлера принимает более простой вид.
Итак, вероятность излучения электроном с энергией Е фотона с энергией Е′ в интервале
(Е′, Е′+dЕ′) в поле атомных ядер на 1см пути в веществе (Z,A,ρ) будет:

При прохождении вблизи атома электрон будет испытывать торможение не только в поле ядра, но и в поле атомных электронов. Учитывается этот эффект путем следующих рассуждений.
а) В поле одиночного заряда ( Z = 1, т.е. в поле ядра водорода или протона)

б) Заряд электрона по абсолютной величине равен заряду протона. Поэтому можно приближенно считать, что вероятность излучения в поле электрона такая же, как и в поле протона:
 = =
 . .
в) В атоме Z электронов, и на каждом из них возможно торможение (независимые события). Поэтому вероятность торможения на всех Z электронах атома получается суммированием Z раз по
 , т.е.
Z· , т.е.
Z· . .
г) Таким образом полная вероятность излучения от взаимодействия со всем атомом будет
 Z2 + Z2 +
 Z = Z =
 ·Z(Z+1), и формула Бете - Гайтлера приобретает вид: ·Z(Z+1), и формула Бете - Гайтлера приобретает вид:

Коэффициент 4αr2·nZ(Z +1)·ln(183Z-1/3) =
1/t0 имеет размерность cм-1. Поэтому величина t0 называется радиационной единицей длины (еще ее называют t0-единицей, каскадной единицей, лавинной единицей). Величина радиационной единицы длины не зависит от энергии налетающего электрона E и энергии излученного фотона E’, она зависит от рода вещества и его плотности. Для примера в таблице 2.5 приведены для некоторых веществ значения t0.
Радиационная единица длины для смеси веществ, имеющих радиационные единицы ti и весовые доли pi, находится по формуле:
1/t0 = ∑ pi/ti
Tаблица 2.5. Величина t0-единицы и критической энергии ε
| Вещество |
ρ, г/cм3 |
t0,см |
t0, г/cм2 |
ε, МэВ |
| Воздух |
1.29·10-3 |
28.8·103 |
37.1 |
81 |
| Вода |
1.0 |
36.4 |
36.4 |
73 |
| Al |
2.7 |
9.0 |
24.3 |
40 |
| Pb |
11.34 |
0.56 |
6.4 |
7.4 |
Таким образом, если вероятность радиационных потерь энергии относить не к 1 см вещества, а к 1 t0-единице вещества, то оказывается, что вероятность излучения на одной радиационной единице длины во всех веществах будет одинакова

Теперь, когда известна вероятность процесса, можно получить сразу же много физических сведений об этом процессе. Итак, следствия из формулы Бете - Гайтлера для случая полного экранирования.
- Энергетический спектр тормозных фотонов, т.е. распределение излученных фотонов по энергиям, во-первых, является сплошным, а во-вторых,
we(E,E′)dE′ ~ 1/E′ − имеет вид гиперболы, т.е. на единице пути излучается либо много фотонов малой энергии, либо мало фотонов большой энергии.
- Полная излучаемая электроном энергия на единице пути

Отсюда следует, что полная излучаемая на единице пути энергия пропорциональна энергии электрона E.
- Относительная потеря энергии
 постоянна для данного вещества и не зависит от энергии излучающего электрона. (При неполном экранировании относительная потеря энергии слабо возрастает с увеличением E).
постоянна для данного вещества и не зависит от энергии излучающего электрона. (При неполном экранировании относительная потеря энергии слабо возрастает с увеличением E).
- Закон убывания энергии электрона за счет тормозного излучения при прохождении слоя вещества х можно получить при интегрировании дифференциального уравнения dE/E = -dx/t0. В результате получаем уравнение:
E = E0 exp(-x/t0),
где E0 − начальная энергия электрона.
Это соотношение помогает раскрыть смысл радиационной единицы длины t0: при прохождении слоя вещества в 1 t0-единицу ( x = t0 ) энергия электрона в среднем за счет тормозного излучения уменьшается в e раз.
- Дифференциальная вероятность передачи определенной доли энергии E′w(E,E′)dE′ имеет очень простой вид: E′·w(E,E′)dE′ =E′/t0. Это выражение не зависит от энергии фотона E' в рассматриваемом приближении.
На рис.2 .9 приведены дифференциальные потери энергии из-за тормозного излучения на пути в одну радиационную единицу длины в свинце для электронов с энергиями 10 и 10 эВ. Из рисунка видно, что энергия излучения почти с равной вероятностью распределяется между фотонами с большой и малой энергиями, т.е. энергия, передаваемая на единице пути фотонам с энергией в интервале от 0 до 0.5 E, почти равна энергии, передаваемой фотонам в
интервале от 0.5 Е до Е. В первом случае возникает большое число малоэнергичных
фотонов, а во втором − всего один-два фотона высокой энергии.
Следствие этого − большой разброс электронов по энергиям
после первого же акта торможения их в веществе, т.е. электрон может передать
значительную часть своей энергии фотону и сразу затормозиться. В этом ярко
проявляется различие между ионизационными потерями и потерями энергии на
тормозное излучение. Энергия, расходуемая на ионизацию, передастся атомным
электронам, как правило, малыми порциями, и быстро растрачивается на тепловое
движение атомов вещества, т.е. происходит нагрев вещества. Энергия в этом случае
теряется безвозвратно.
При тормозном излучении фотон имеет большую вероятность унести энергию, сравнимую с энергией электрона. В этом случае энергия электрона как бы "перекачивается" к фотонам, а не теряется безвозвратно.
Итак, при торможении электрон может затормозиться сразу, образовав энергичный фотон, или плавно терять энергию, создавая много фотонов. Это обстоятельство приводит к
сильным флуктуациям в радиационных потерях энергии.

Рис.2.9. Дифференциальные потери'энергии на тормозное излучение на одной t0-единице в свинце: 1 − Е = 1010 эВ, 2 − Е = 108 эВ.
Угловое распределение фотонов тормозного излучения существенно зависит от энергии образующих их электронов. В нерелятивистском случае фотоны могут испускаться как вперед, так и назад. Их угловое распределение пропорционально cos2θ , где θ – угол вылета фотона по отношению к траектории тормозящегося электрона.
Чем выше энергия электронов E, тем больше фотонов будет излучаться по направлению движения электронов. В ультрарелятивистском случае ( E
>> mec2 ) фотоны тормозного излучения сильно коллимированы в направлении движения электронов. Угловое распределение фотонов имеет вид:

Средний угол вылета фотонов равен < θ > = mec2/E. Т.е. чем выше энергия электронов E, тем острее конус излучения.
В электронных ускорителях типа бетатрона или синхротрона при торможении пучка быстрых электронов на мишени возникает гамма-излучение
в виде узкого пучка по направлению порождающих его электронов.
Тормозное излучение − это основной метод получения пучков
фотонов высокой энергии, с помощью которых изучаются электромагнитная структура элементарных частиц и атомных ядер, фоторождение элементарных частиц и другие процессы взаимодействия излучения с веществом.
Сравнение удельных потерь энергии электронов на излучение и ионизацию показывает, что они по-разному зависят от энергии электронов и параметров среды.
Радиационные потери сильнее зависят от номера вещества, чем ионизационные (~Z2 вместо ~ Z), и сильнее зависят от энергии электрона.
Как уже отмечалось, радиационные потери быстро растут с возрастанием энергии электрона, в то время как ионизационные потери остаются практически постоянными при Е
>> mec2. Таким образом, при больших энергиях электронов потери на излучение оказываются гораздо более существенными, чем ионизационные потери.

Рис.2.10. Относительные потери энергии электрона на одной
t0-единице пути на ионизацию:
(1 – в свинце, 2 – в воздухе) и на излучение (3 – в свинце, 4 – в воздухе) |
На рис. 2.10 показаны относительные потери энергии на излучение и ионизацию на радиационной единице длины в воздухе и свинце. Возрастание относительных потерь на излучение до энергии электрона Е ~ 109 эВ обусловлено эффектом неполного экранирования атомными электронами поля ядра,
поэтому относительные потери энергии при торможении слабо возрастают с энергией
электрона, достигая единицы при энергии Е ~ 109 эВ.
Количественное сравнение потерь энергии утрарарелятивистскими
электронами на ионизацию и тормозное излучение приводит к соотношению

где Сonst ≈ 600 МэB, если энергию электрона E измерять в МэВ.
Энергия электронов, при которой потери на излучение становятcя равными потерям на ионизацию, называетcя
критической энергией ε. Она разная для разных веществ
ε = Const / Z ~ 600 МэВ /Z.
В табл.2.5 приведены величины ε для разных веществ. Итак, при Е < ε ионизационные потери больше тормозных, при
E > ε преобладают потери на излучение, а при Е = ε: (dE/dx)рад
= (dE/dx)ион. Следовательно, получаем Z·e =
Const и (dE/dx)рад /(dE/dx)ион
= E/ε. Т.к. (dE/dx)рад
= E/t0, то
(dE/dx)ион = ε/E · (dE/dx)рад
= ε/E · E/t0 = ε/t0.
Если E принять за единицу пути радиационную единицу длины, т.е. положить t = x/t0, то
(dE/dx)ион = ε.
Следовательно, численно критическая энергия равна ионизационным потерям на одной радиационной единице пути t0.
2.10. Излучение Вавилова - Черенкова
История вопроса. Очень слабое голубовато-белое свечение прозрачных веществ, находившихся вблизи сильных радиоактивных источников, наблюдалось многими специалистами, изучавшими радиоактивность. Так, в 1910 г.
М. Кюри обнаружила, что бутыли с концентрированными растворами радия испускали этот таинственный свет. Все это произошло задолго до того, как стала ясна природа этого свечения.
Первая попытка изучить это явление была предпринята в 1926-28 годах Л. Малле, работа которого несправедливо игнорирована и забыта. Малле обнаружил, что прозрачные тела, помещенные около радиоактивного источника, всегда имеют одинаковую голубовато-белую окраску. Он нашел, что спектр излучения – непрерывный и отличается от люминесценции. К сожалению, Малле не продолжил своего исследования и не попытался найти объяснения этого явления. Оно было забыто до 1934 года, когда
П.А.Черенков начал серию опытов, продолжавшихся до 1938 г.
Будучи аспирантом С.И. Вавилова П.А. Черенков исследовал люминесценцию растворов ураниловых солей под действием гамма-излучения радия. П.А. Черенков обнаружил свечение, которое нельзя было объяснить обычным механизмом возбуждения флуоресценции.
Флуоресценция возникает в случае перехода атомов из возбужденных энергетических состояний в основные. Длительность флуоресцентного высвечивания ~ 10-10 с, и на вероятность перехода можно воздействовать, изменяя температуру среды или добавляя определенные гасящие вещества. Однако обнаруженное свечение подавить не удавалось – это была не флуоресценция.
Количественные измерения проводились Черенковым методом визуальной фотометрии по порогу зрения (методом гашения). Этот метод был разработан в лаборатории Физического института АН СССР (ФИАН) С.И. Вавиловым и Брунбергом. Метод гашения основывался на том, что сумеречное зрение имеет зрительный порог и
пороговая энергия постоянна для данного наблюдателя. После адаптации на темноту,
продолжавшуюся от 1 до 1.5 часов, светочувствительность глаза повышалась в ~104
раз. Это позволяло проводить измерения свечения методом визуальной фотометрии,
причем для визуального гашения света использовался оптический клин.
Выводы исследований сказались неожиданными:
1) свечение не является флуоресценцией;
2) свечение вызывается не гамма-квантами, а быстрыми комптон- и фотоэлектронами, так как при наложении магнитного поля менялась поляризация свечения;
3) интенсивность излучения не зависит от заряда среды Z, т.е.
оно не может быть радиационного (тормозного) происхождения;
4) излучение направлено под определенным углом к направлению движения частицы;
5) спектр свечения оказался сплошным. Это обстоятельство оказалось решающим для выяснения его природы и создания теории этого явления. Объяснение этого свечения было найдено в 1937 г.
И.Е. Таммом и
И.М. Франком. За открытие и объяснение этого явления И.Е. Тамму, И.М. Франку и П.А.Черенкову в 1958 г. была присуждена Нобелевская премия.
Итак, в 1937 г. Тамм и Франк показали, что свечение Вавилова -Черенкова и качественно и количественно может быть объяснено с помощью представлений как классической, так и квантовой электродинамики, из которых следует, что равномерно движущийся в среде заряд должен излучать свет, если его скорость превышает фазовую скорость света в этой среде, т.е. если V >
c/n. Рассмотрим эти соображения.
1. Квантовый подход. Если заряд движется В однородной среде прямолинейно и равномерно со скоростью V, то и его электромагнитное поле переносится вместе с ним, т.е. излучаемая им волна имеет вид: exp
(i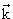 ·( ·(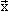 − −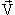 t), где t), где 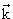 − волновой вектор, характеризующий направление распространения световой волны. Частота этой волны (множитель при t, в показателе экспоненты) определяется равенством: ω = − волновой вектор, характеризующий направление распространения световой волны. Частота этой волны (множитель при t, в показателе экспоненты) определяется равенством: ω = 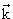 · ·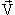 = kV·cos
θ, где θ − угол между направлением распространения волны = kV·cos
θ, где θ − угол между направлением распространения волны 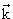 и скоростью заряда и скоростью заряда
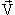 . Но частота всякой электромагнитной волны в среде связана с ее волновым вектором соотношением ω = сk/n, где
n − показатель преломления для данной волны в однородной среде. Следовательно, . Но частота всякой электромагнитной волны в среде связана с ее волновым вектором соотношением ω = сk/n, где
n − показатель преломления для данной волны в однородной среде. Следовательно,
сk/n = kV·cos θ и cos
θ = c/nV = 1/nβ.
Полученное соотношение определяет угол, между направлением движения частицы и направлением распространения излучаемой ею волны. Естественно, что реально волна излучается лишь в том случае, если cos θ ≤ 1, т.е. должно выполняться соотношение: V ≥
c/n – скорость заряженной частицы превосходит фазовую скорость света в среде.
Отсюда следует и другой важный вывод: так как β ≤ 1 а nβ >1, то, следовательно, излучение возможно лишь в средах с показателем преломления n > 1.
2. Классический подход. Заряженная частица, двигаясь в среде с показателем преломления n, вызывает вдоль своего пути поляризацию атомов среды, которые на короткое время превращаются в диполи. Колебание диполей, сопровождающее возвращение поляризованных атомов в исходное состояние, приводит к появлению электромагнитного излучения.

Рис.2.11. Поляризация, возникающая в среде при прохождении заряженной частицы:
а – при скорости V < c/n; б – при V > c/n.
Если частица движется со скоростью V, меньшей скорости распространения света в среде с/n, то поляризация возникает и перед частицей и за ней (рис.2.11а). В целом поляризация сферически симметрична, и излучение всех диполей в сумме полностью скомпенсировано. Если частица движется со скоростью V > с/n, то поляризация возникает позади частицы (рис.2.11б) (эффект запаздывающей поляризации среды), в результате чего диполи ориентируются преимущественно в сторону движения частицы. В этом случае должно существовать такое направление, по которому может возникнуть когерентное излучение диполей, так как волны, испущенные в разных местах пути частицы, могут оказаться в одинаковой фазе.

Рис.2.12. Построение Гюйгенса, иллюстрирующее когерентность |
Таким образом в отдаленных точках будет существовать результирующее поле, причем излучение будет наблюдаться лишь под определенным углом θ относительно траектории частицы (АВ), при котором волны когерентны и образуют плоский волновой фронт
(CB) (рис.2.12). Возникновение черенковского свечения аналогично появлению волн
за пароходом или ударных волн за сверхзвуковым самолетом.
Направление распространения излучения легко найти. Если за время t частица, двигаясь со скоростью V, прошла путь АВ = t·V , то за то же самое время волна, испущенная диполем в точке А, прошла путь АС = t·c/n . Так как АС = АВ·соs
θ , то c/n · t =V·t · cos
θ, откуда получаем уже знакомое нам соотношение: cos θ =
1/βn.
Характерные особенности ченковского излучения
1) Для среды с показателем преломления n можно найти диапазон скоростей частицы β, при котором наблюдается черенковское свечение. Так как сos
θ = 1/βn, то при θmin = 0, cos θmin =1 и β = 1/n. С другой стороны скорость частицы не может превышать с, т.е. βmax = 1. Следовательно, cos
θmax =1/n. Итак, частица будет создавать черенковское излучение, если ее скорость находится в диапазоне:
1/n ≤ β ≤ 1.
При этом угол θ, под которым наблюдается это
свечение относительно траектории частицы, растетет с увеличением скорости
частицы в диапазоне 0 ≤ θ ≤ arccos 1/n и этот угол θ одинаков для
частиц любых зарядов и масс, движуихся в среде со скоростью β > 1/n.
2). Для величины энергии излучения, т.е. для величины энергии, потерянной на черенковское излучение частицей с зарядом ze, скоростью β на единице пути в среде с показателем преломления n, И.Е.Тамм и И.М.Франк получили следующее выражение:

Из этого выражения видно, что излучаемая на единице пути энергия:
- a) пропорциональна квадрату заряда частицы (ze)2,
- b) не зависит от массы частицы М,
- c) не зависит от Z атомов среды,
- d) зависит от показателя преломления среды n(ω); и
- e) пропорциональна частоте излучения ω.
В реальной cреде n зависит от частоты излучения ω, т.е. среда всегда обладает дисперсией, так что излучение ограничено областью, для которой n(ω) >1. На рис.2.13 изображена дисперсии типичной прозрачной среды в разных
диапазонах спектра электромагнитного излучения.

Рис.2.13. Кривая дисперсии типичной прозрачной среды в разных диапазонах спектра электромагнитного излучения:
1 − рентгеновская область; 2 − далекая ультрафиолетовая; 3 − близкая ультрафиолетовая;
4 − видимая; 5 − близкая инфракрасная; 6 − далекая инфракрасная область;
7 − радиочастотная,
ε − диэлектрическая постоянная среды
Так как черенковское излучение образуется только при n > 1, то, следовательно, оно возможно:
- a) в области близкого ультрафиолета и видимого света, т.е. в диапазоне 3500 Å- 7000 Å;
- b) в области далекого инфракрасного излучения;
- c) в области радиочастот.
Черенковское излучение полностью отсутствует в рентгеновском диапазоне и в области далекого ультрафиолета, так как для них. n(ω) < 1.
Так как спектральное распределение излучения имеет вид:

то наибольшая энергия выделяется в ультрафиолета и голубого видимого света. свечение имеет голубой цвет.
3). Зная энергию, переданную черенковское излучение -dE/dx , можно найти число испущенных на этом пути фотонов dN/dx (так как dE = dN·ħω ).
Итак, число фотонов в интервале частот (ω, ω+dω), испускаемых на единице пути в среде с показателем
преломления n частицей с зарядом ze и скоростью βc под углом θ к траектории частицы, по теории Франка-Тайма, имеет вид:

Следствия из этого выражения:
- а) число фотонов растет с увеличением скорости частицы от 0 (при β = 1/n) до максимального числа фотонов (при β = I ), равного
-

- b) число фотонов на единице пуги dx и в единице частотного интервала dω
не зависит от их частоты ω, т.е. спектр черенковского свечения равномерен по
частотам.
Так как энергия фотонов равна ћω, то основная энергия
излучения сконцентрирована в наиболее коротковолновой части спектра. Поэтому
при практическом использовании эффекта Черенкова выгодно выбирать среды,
прозрачные для высоких частот;
- c) так как основная энергия выделяется в диапазоне длин волн от 3500 Å до 7000 Å, то на 1 см пути частицей излучается фотонов:
-
 

- d) интенсивность излучения прямо пропорциональна квадрату заряда частицы;
- e) интенсивность свечения прямо пропорциональна sin2θ, т.е.
существенно зависит от величины угла θ. Для одной и той же среды при
увеличении скорости частицы увеличивается θ, и интенсивность излучения тоже
растет.
4. Доля энергии, теряемая заряженной частицей на черенковское
излучение, вообще незначительна и составляет всего несколько процентов от других видов энергетических потерь.
Отличия излучения Вавилова-Черенкова от тормозного излучения
- Черенковское излучение возникает при движении частиц с постоянной скоростью. Тормозное излучение − при движении заряженных частиц с ускорением.
- Черенковский свет испускается средой, а тормозное излучение − частицей.
- Черенковский свет − это когерентное излучение большого числа атомов. Тормозное излучение возникает при взаимодействии
с отдельным атомом (ядром).
- Черенковское излучение в основном состоит из мягких фотонов видимого или ультрафиолетового света, а тормозные фотоны − жесткие, энергия которых сравнима с энергией частицы.
- Интенсивность черенковского света не зависит от массы М частицы, тормозного излучения
~ 1/M2
- Интенсивность черенковского света не зависит от характеристик среды (Z,A), тормозного ~Z2.
- Угол θ черенковского излучения увеличивается с увеличением энергии (скорости) частицы, а тормозного − уменьшается.
В излучении Вавилова-Черенкова впервые проявилась связь ядерной физики и оптических свойств вещества (n). Характерные свойства излучения Вавилова - Черенкова определяют главным образом три величины: заряд частицы, скорость частицы и показатель преломления света средой. Есть и другие явления, связанные с оптическими свойствами среды, т.е. явления, в которых оптические свойства среды существенны для излучения быстрой частицы. К ним относится переходное излучение.
2.11. Переходное излучение
Переходное излучение – это излучение электромагнитных волн равномерно и прямолинейно движущейся частицей при пересечении ею границы двух сред с разными показателями преломления, т.е. отличающихся скоростью распространения в них света. Такое излучение наблюдается экспериментально и называется
переходным.
При движении частицы в однородной среде ее поле перемещается вместе с ней. Характер поля определяется зарядом, скоростью частицы и свойствами среды. Когда частица переходит в другую среду, ее поле меняется, что сопровождается излучением электромагнитных волн.
Пример 1. Пусть быстрая заряженная частица попадает из вакуума в идеальный проводник. В момент пересечения границы раздела электрическое поле заряда во внешнем пространстве исчезает и
возникает электромагнитное излучение. Если еще при этом энергия частицы очень
велика, и не происходит заметного рассеяния и изменения скорости, то частицу
можно считать равномерно движущейся. Таким образом возникает излучение при равномерном движении частицы, которое существенно зависит от оптических свойств среды.
Переход из вакуума в идеальный проводник (некоторые металлы) – это только частный случай возникновения переходного излучения. Излучение должно возникать каждый раз, когда частица пересекает границу двух сред с разными оптическими характеристиками.
Пример 2. Наблюдаемое свечение анода в катодных трубках под действием падающих электронов оказалось сплошным (Лилиенфельд, 1919 г.), хотя его пытались отнести за счет люминесценции и других видов тормозного излучения. Все были убеждены, что при равномерном движении заряженной частицы излучения происходить не должно. Это представление отпало после появления теории эффекта Вавилова
- Черенкова.
Существование переходного излучения было предсказано
В.Л. Гинзбургом и
И.М. Франком в 1945 г. – задолго до его экспериментального наблюдения. Ими было показано, что излучение должно возникать по обе стороны от границы раздела, "вперед" и "назад".
1. Переходное излучение "назад". Теория на основе уравнений электродинамики и расчеты показали:
- a) "назад" (т.е. в среду, из которой частица выходит) излучаются электромагнитные волны видимого диапазона независимо от скорости частицы,
- b) интенсивность этого излучения мала (1 фотон на 100 падающих частиц),
- c) при малых энергиях частицы (v << c) энергия, излучаемая назад, растет пропорционально энергии частицы, т.е. ∆E ~ E.
При увеличении скорости частицы (v → c) излучаемая энергия ∆E ~ ln E , т.е. рост потерь энергии замедляется.
В 1958 г. излучение "назад" наблюдалось на эксперименте: при падении пучка частиц из вакуума на металл возникало яркое белое светящееся пятно в том месте, куда падает пучок. Экспериментально найденные характеристики хорошо согласовывались с предсказанными.
Определение характеристик переходного излучения ("назад") в оптической области со временем стало настолько точным, что по его параметрам (по спектру, поляризации, угловому распределению) можно судить об оптических свойствах поверхностей, что нашло
применение на практике.
2. Переходное излучение ("вперед") оказалось очень перспективным для наблюдения частиц сверхвысоких энергий.
- а) Частотный спектр переходного излучения оказался сплошным в очень широком диапазоне: от оптического до рентгеновского, причем максимальная частота его прямо пропорциональна энергии частицы Е, т.е. основная часть излучения находится в рентгеновском диапазоне:
ωmax = ω0·(E/Mc2) = ω0γ, где M − масса частицы,
γ − ее лоренц-фактор, а ω0 = (4πnee2/me)1/2 −
плазменная частота среды.
- b). При больших энергиях частиц Е энергия, передаваемая ими в переходное
излучение
-

- где z- заряд частицы. Например, электрон с энергией 10 ГэВ при выходе вперед из плотной среды в газ излучает фотон с энергией 10
кэВ, т.е. фотон в рентгеновском диапазоне (РПИ − рентгеновское переходное излучение).
- c). Испущенное "вперед" излучение распространяется под малыми углами к направлению движения частицы:
-

- т.е. < θ> ~ Mc2/E.
- d). Интенсивность излучения, т.е. число фотонов на границу раздела очень мала:
~ 2/3·α·z2 ≈ 0.5%·z2.
Эти свойства рентгеновского переходного излучения (~1/γ, ∆Е ~ γz2)
используются для идентификации частиц высоких энергий при γ > 103, т.е. когда применение других методов затруднительно. Однако, следует отметить и отрицательные стороны РПИ: очень большие флуктуации и малую интенсивность излучения. Низкая абсолютная интенсивность РПИ привела к необходимости использовать слоистые или пористые радиаторы.
Слоистый радиатор состоит из нескольких сотен тонких (5-100 мкм) слоев легкого вещества (Li, Be, лавсан и др.) вперемежку с воздушными промежутками (или вакуумом) в 0.1 – 2 мм. При этом существует определенное расстояние и внутри плотного вещества и в промежутке, необходимое для возникновения переходного излучения, – зона формирования. Дело в том, что характерной особенностью переходного излучения из стопки пластин является интерференция излучения на двух границах одной пластины, а также от различных пластин, зависящая от материала пластин, частоты излучения ω, величины лоренц-фактора частицы γ, и угла излучения θ.
Результатом этой интерференции является возникновение когерентной длины
излучения или зоны формирования РПИ, причем величина этой зоны как в плотной среде
– "a" (фольга, майлар, полиэтилен), так и в промежутке – "b" (вакуум, воздух) получается равной:

Толщина слоев "a" и "b" должна быть больше величины зоны формирования, иначе интенсивность РПИ резко уменьшается за счет деструктивной интерференции излучения.
Пористый радиатор – гранулированный LiH, легкий пенопласт, полипропиленовое или углеродное волокно. Толщина волокна, фольги и ширина зазоров должны удовлетворять требованиям к длине формирования. Пористый радиатор генерирует на 10 -15 % меньше фотонов, чем слоистый из того же материала.
Использование РПИ для детектирования заряженных частиц имеет некоторые преимущества перед другими методами:
1) идентифицирует частицы с энергиями 102 - 103
ГэВ. т.е. γ ~ 103. других методов в этой области энергий нет;
2) идентифицирует частицы "на лету", т.е. частица сохраняется
как таковая в отличие от других методов, при которых она либо поглощается, либо
рассеивается, либо тормозится и пр.
Вопросы и задачи к главе 2
1. Мюон с кинетической энергией 10 МэВ пролетает на расстоянии 10-9 см от свободного электрона. Какую энергию он потеряет?
2. Протон с кинетической энергией 100 МэВ пролетает на расстоянии 10-9 см от свободного электрона. Какую энергию он потеряет?
3. Сравнить удельные ионизационные потери энергии для α-частиц и для протонов с энергией
100 МэВ при прохождении через алюминий (Z = 13, A = 27, ρ = 2.7 г/см3) и свинец (Z = 82, A = 207, ρ = 11.3 г/см3).
4. Сравнить пробеги протонов и мюонов с одинаковой энергией 50 МэВ в алюминии.
5. Посчитать плотность δ-электронов на пути релятивистского протона в воздухе (Z = 7, A = 14,
ρ = 1.29·10-3 г/см3) и алюминии (Z = 13, A = 27, ρ = 2.7г/см3).
6. Найти угол многократного рассеяния в воздухе и алюминии для протона с энергией 100 МэВ и 100 ГэВ.
7. Какая в среднем энергия останется у монохроматических протонов с энергией 100 МэВ после прохождения пластины из алюминия толщиной 1 см?
8. Поток электронов с кинетической энергией 100 МэВ падает на свинцовую пластинку толщиной
1 см. Какова средняя энергия электронов при выходе из пластинки (t0 = 0.56см)?
9. Какой средний угол вылета фотонов при торможении электронов с энергией 100 МэВ?
10. Найти пороговую энергию эффекта Вавилова - Черенкова для р, π, е в стекле (n = 1.8), плексигласе (n = 1.5), воде (n = 1.33), и в воздухе (n = 1.0003).
11. Определить кинетическую энергию электронов, если черенковский свет от них в плексигласе
(n = 1.5) наблюдается под углом 300 к направлению их движения.
12. Определить интенсивность потока черенковских фотонов при прохождении 1 см плексигласа для условия, приведенного в задаче 11.
  

|


![]() =F·cos
α = F·b/(x2 + b2)1/2 и, следовательно,
=F·cos
α = F·b/(x2 + b2)1/2 и, следовательно,
![]() = z e2·b/(x2 + b2)3/2. Перпендикулярная составляющая переданного импульса получается при интегрировании по всему времени взаимодействия
= z e2·b/(x2 + b2)3/2. Перпендикулярная составляющая переданного импульса получается при интегрировании по всему времени взаимодействия
 , где dt = dx/V
и
, где dt = dx/V
и

![]()






![]()



![]()






 − релятивистская кинетическая энергия электрона.
− релятивистская кинетическая энергия электрона.





















 с электроном −
с электроном −

 с электронами −
с электронами −


 .
.














