Деление ядер
В области тяжелых ядер (Z > 90)
существенную роль играет деление атомных ядер.
Спонтанное деление атомных ядер было открыто в
1940 году Г. Флеровым и К. Петржаком. Исходя из
массовой формулы Вайцзеккера, можно оценить
величину энергии Q, выделяющейся в процессе
деления

|
(10.1) |
(эта оценка получена для случая, когда
отношение масс легкого и тяжелого осколков
деления составляет 2:3). Отсюда следует, что
Q > 0, если Z2/A > 17. Величина Z2/A
называется параметром деления. Деление
оказывается энергетически выгодным для ядер с
Z > 50. Однако, потенциальный барьер
препятствует мгновенному самопроизвольному
делению ядер. В процессе деления меняется форма
ядра, что приводит к изменению кулоновской и
поверхностной энергий. Вероятность спонтанного
деления растет с увеличением параметра деления Z2/A,
то есть при переходе к более тяжелым ядрам. При
переходе от 92-го элемента к 104 вероятность
спонтанного деления увеличивается примерно в 1020
раз.
Барьер деления играет решающую роль в
стабильности тяжелых ядер. Согласно капельной
модели, ядра с Z2/A > 49 не должны
существовать, так как для этих ядер величина
потенциального барьера равна нулю и такие ядра
должны делиться в течение характерного ядерного
времени (10-22 с). Однако более детальные
расчеты, учитывающие влияние оболочечных
эффектов на свойства атомных ядер, указывают на
качественно новые явления.
- В области Z > 100, N > 126 можно ожидать
появление следующих магических чисел по
протонам и нейтронам, что приведет к
дополнительной устойчивости атомных ядер и
увеличению их времени жизни в этой области N-Z
диаграммы. Можно ожидать повышения устойчивости
атомных ядер в районе Z = 114.
- Резкие изменения положения одночастичных
уровней с изменением величины деформации ядра
приводят к перераспределению плотности
одночастичных состояний по сравнению со
сферическими ядрами. Следствием этого является
то, что в основном состоянии атомные ядра имеют
форму отличную от сферически симметричной, то
есть деформированы. Деформация атомных ядер
является еще одной дополнительной степенью
свободы, обеспечивающей повышенную устойчивость
атомных ядер
- Для тяжелых ядер барьер деления имеет двугорбую
форму.
Двугорбый барьер деления позволил объяснить
такие явления как спонтанное деление изомеров,
резонансы в подбарьерном делении и ряд других
экспериментально наблюдаемых фактов.
Одним из важных физических
результатов, полученных в реакциях деления под
действием тяжелых ионов, является обнаружение
важной роли "вязкости" ядерной материи. В
результате взаимодействия тяжелого иона с ядром
образуется компаунд-ядро, которое затем
распадается по различным каналам. Основными
каналами распада компаунд-ядра являются эмиссия
легких частиц (в основном нейтронов, протонов, a
-частиц) и деление. Сечение подбарьерного слияния
тяжелого иона и ядра-мишени плохо описывается в
модели простого одномерного кулоновского
барьера. Это обусловлено тем, что в модели
необходимо учитывать деформации сталкивающихся
ядер, а также возможность передачи частиц от
одного ядра другому.

Рис. 11.18. Функция возбуждения для полного
слияния (черные точки) и неполного слияния
(светлые точки) в реакции 12С + 160Gd |
На рис. 11.18 показана функция
возбуждения для полного слияния (черные точки) и
неполного слияния (светлые точки) в реакции 12С + 160Gd.
Реакции неполного слияния сопровождаются
испусканием предравновесных частиц
преимущественно в направлении первичного пучка.
Однако ряд принципиальных вопросов физики
деления под действием тяжелых ионов остается
пока не решенным. Для надежной интерпретации
процесса деления необходима информация о
конкуренции между процессом деления и процессом
испарения легких фрагментом из компаунд-ядра.
Необходимо исследовать массовые и зарядовые
распределения осколков деления, знать их
кинетические энергии, множественности нейтронов
и протонов, испускаемых до деления из
компаунд-ядра. Так как деление под действием
тяжелых ионов связано с большим угловым моментом
образующейся системы, простая модель жидкой
капли не применима. Угловой момент образующейся
составной системы приводит к уменьшению барьера
деления. Барьер деления Ef (J)
определяется как разность энергий состояний в
равновесной и седловой точках.

где Jседл, Jравн - моменты инерции
седловой и равновесной конфигурации, J1 -
угловой момент в седловой точке, J2 - угловой
момент в равновесной точке.

Рис. 11.19. Зависимость отношения делительной Гf
и нейтронной Гn ширин от энергии
возбуждения E* и величины углового момента J
компаунд-ядра 168Yb |
Величина барьера деления Ef(J)
уменьшается с увеличением J, кроме того надо
учесть, что Jседл > Jравн. На
рис. 11.19 показана зависимость отношения
делительной Гf и нейтронной Гn ширин
от энергии возбуждения E* и величины
углового момента J компаунд-ядра 168Yb. Кривые
соответствуют постоянным значениям отношения Гf/Гn,
указанных цифрами. Отчетливо проявляется эффект
увеличения этого отношения с ростом величины
вращательного момента. Толстая сплошная кривая в
нижней части рисунка соответствует суммарной
энергии барьера деления и вращательной энергии.
На рис. 11.20 показаны сечения реакции слияния
(светлые кружки) и реакции деления (темные кружки)
в зависимости от энергии в системе центра масс
сталкивающихся ионов. Здесь же показаны
результаты расчетов, выполненных по программе
ALERT1, достаточно хорошо описывающие
экспериментальные данные. Пунктирная кривая
соответствует различным вращательным моментам
образующейся компаунд-системы.
Информацию о времени жизни
компаунд-системы от момента образования до ее
развала на два осколка можно извлечь из
измерений множественности нейтронов
предшествующих делению.

Рис. 11.20. Сечения реакции слияния (светлые
кружки) и реакции деления (темные кружки) в
зависимости от энергии в системе центра масс
сталкивающихся ионов |
На рис. 11.21 и 11.22 показаны полная
множественность и множественности
предделительных нейтронов в зависимости от
энергии возбуждения ядра. Из приведенных данных
были получены оценки времени перехода от
седловой точки к точке разрыва, составляющие
величину ~(14-40)·10-21c. По
сравнению с делением слабовозбужденного
компаунд-ядра процесс деления под действием
тяжелых ионов, когда образуется сильно
возбужденное вращающееся ядро, происходит
гораздо быстрее.
 Рис. 11.21. Полная множественность
нейтронов в зависимости от энергии возбуждения,
реализующейся при делении Рис. 11.21. Полная множественность
нейтронов в зависимости от энергии возбуждения,
реализующейся при делении |
 Рис. 11.22. Множественность
предделительных нейтронов в зависимости от
энергии возбуждения компаунд-системы Рис. 11.22. Множественность
предделительных нейтронов в зависимости от
энергии возбуждения компаунд-системы |
Энергетические спектры нейтронов
также сильно зависят от энергии возбуждения и
момента испускания нейтронов из
компаунд-системы. На рис. 11.23 показаны спектры
нейтронов вылетающих под разными углами
относительно направления первичного пучка 12С
падающего на мишень 175Lu. Сплошная кривая
аппроксимирует суммарный спектр нейтронов,
короткие штрихи - долю спектра нейтронов,
испущенных из компаунд-ядра до разрыва,
штрих-пунктирные и пунктирные кривые показывают
долю спектра нейтронов, испущенных из обоих
осколков, длинные штрихи - предравновесная
составляющая части спектра.

Рис. 11.23. Спектры нейтронов, вылетающих под
разными углами относительно направления
первичного пучка 12С, падающего на мишень 175Lu |
|

Рис. 11.24. Спектр
 -квантов образующихся в реакции
16O+208Pb
при энергии налетающих ионов 16O: а - 100, б - 120
и в - 140 Мэв -квантов образующихся в реакции
16O+208Pb
при энергии налетающих ионов 16O: а - 100, б - 120
и в - 140 Мэв |
Наряду с нейтронами из компаунд-ядра
и осколков деления испускаются  -кванты. На рис. 11.24 показан
спектр γ-квантов,
образующихся в реакции 16O + 208Pb
при энергии налетающих ионов 16O: а - 100, б - 120
и в - 140 Мэв. Наряду с малоэнергетическими
фотонами наблюдаются фотоны с энергией >10Мэв от
распада гигантского дипольного резонанса,
который возбуждается как в компаунд-ядре, так и в
осколках деления. Энергии ГДР для
компаунд-систем ниже, чем для осколков деления,
что находится в хорошем согласии с данными,
полученными в реакциях под действием γ-квантов. -кванты. На рис. 11.24 показан
спектр γ-квантов,
образующихся в реакции 16O + 208Pb
при энергии налетающих ионов 16O: а - 100, б - 120
и в - 140 Мэв. Наряду с малоэнергетическими
фотонами наблюдаются фотоны с энергией >10Мэв от
распада гигантского дипольного резонанса,
который возбуждается как в компаунд-ядре, так и в
осколках деления. Энергии ГДР для
компаунд-систем ниже, чем для осколков деления,
что находится в хорошем согласии с данными,
полученными в реакциях под действием γ-квантов.
Динамика деления атомных ядер связана
с поведением сверхплотной среды, каковой
является ядерная материя. Другой особенностью
атомных ядер является то, что число частиц в ядре
относительно невелико. Поэтому взаимодействие
нуклонов с ядерной поверхностью оказывается
существенным. Обусловлено это тем, что среднее
ядерное поле формируется самими нуклонами (в
отличие от атома, где кулоновское поле
формируется центральным ядром), поэтому в ядре
возможны различные виды коллективных движений:
вращение, колебание, возбуждение гигантских
резонансов.

Рис. 11.25. Влияние диссипации на формы в точке
разрыва для делящихся ядер с различными Z2/A |
Характеристики ядерной
материи и, в частности, вязкость ядерной среды
оказывают существенное влияние, например, на
динамику процесса деления и, в частности, на
форму ядра в точке разрыва. На рис. 11.25 показана
эта зависимость для различных ядер в двух
случаях - нулевой и бесконечной вязкости.
На рис. 11.26 показана зависимость
средней множественности предделительных
нейтронов для реакции 16O + 142Nd от
коэффициента 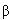 ,
описывающего затухание в ядерной среде. Видно,
что простая статическая модель (SM), показанная
прямыми пунктирными линиями, не описывает
экспериментальные данные (заштрихованный
участок). Для описания экспериментальных данных
необходимо дополнительно учесть влияние
затухания в ядерной среде (пунктирная линия Т) и
испускание нейтронов при переходе от седловой
точки к точке разрыва (сплошная линия SST).
Приведенные результаты показывают как меняются
характеристики и поведение ядерной системы в
промежуточной области между образованием
низкоэнергетической компаунд-системы и системы,
образующейся в результате глубоконеупругого
взаимодействия. ,
описывающего затухание в ядерной среде. Видно,
что простая статическая модель (SM), показанная
прямыми пунктирными линиями, не описывает
экспериментальные данные (заштрихованный
участок). Для описания экспериментальных данных
необходимо дополнительно учесть влияние
затухания в ядерной среде (пунктирная линия Т) и
испускание нейтронов при переходе от седловой
точки к точке разрыва (сплошная линия SST).
Приведенные результаты показывают как меняются
характеристики и поведение ядерной системы в
промежуточной области между образованием
низкоэнергетической компаунд-системы и системы,
образующейся в результате глубоконеупругого
взаимодействия.
|

Pис. 11.26 Зависимость средней множественности
предделительных нейтронов для реакции 16O + 142Nd
от коэффициента b, описывающего затухание в
ядерной среде |
Запаздывающее деление
В тяжелых ядрах, удаленных от полосы
β--стабильности,
энергия β-распада
может быть сравнима с величиной барьера деления
дочернего ядра. Для таких ядер β-распад на возбужденные
состояния может сопровождаться делением. Для
того, чтобы наблюдалось запаздывающее деление,
необходимо выполнение соотношение Qb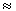 Qf. Если это условие
выполняется, собственное время деления из
возбужденного состояния будет составлять ~10-14 c.
При таких временах деление оказывается вполне
конкурентноспособным с γ-распадом из возбужденных
состояний. Наиболее благоприятная область, в
которой можно наблюдать запаздывающее деление,
будет определяться условиями Qf. Если это условие
выполняется, собственное время деления из
возбужденного состояния будет составлять ~10-14 c.
При таких временах деление оказывается вполне
конкурентноспособным с γ-распадом из возбужденных
состояний. Наиболее благоприятная область, в
которой можно наблюдать запаздывающее деление,
будет определяться условиями
T1/2(β) < T1/2( ); T1/2(β) < T1/2(спонтанное деление). ); T1/2(β) < T1/2(спонтанное деление).
То есть период полураспада ядра по
отношению к β-распаду
должен быть меньше, чем период a -распада и
спонтанного деления. Явление запаздывающего
деления было обнаружено в Дубне [В.И. Кузнецов,
Н.К. Скобелев, Г.Н. Флеров. Я.Ф. 1967 Т5, с.1136] при
облучении мишеней из 209Bi ускоренными
ионами 22Ne и 230Th ионами 10B.
Наблюдалось деление ядер с аномально
малыми для данных ядер периодами полураспада
~1-3 мин. Этот результат противоречил оценкам
периода полураспада ~108-1010 лет,
которые получались при делении нечетно-нечетных
ядер  и и  , исходя из высоты барьера деления. В то
же время из оценок, полученных на основе масс
атомных ядер, следовало, что энергии возбуждения
ядер , исходя из высоты барьера деления. В то
же время из оценок, полученных на основе масс
атомных ядер, следовало, что энергии возбуждения
ядер  и и  , образующихся в результате e-захвата,
сравнимы с высотой барьера и в некоторых случаях
превышают его. Наблюдаемое на эксперименте
увеличение вероятности деления примерно в 1015раз
было интерпретировано как запаздывающее деление
четно-четных ядер , образующихся в результате e-захвата,
сравнимы с высотой барьера и в некоторых случаях
превышают его. Наблюдаемое на эксперименте
увеличение вероятности деления примерно в 1015раз
было интерпретировано как запаздывающее деление
четно-четных ядер  и и  из возбужденных состояний,
образующихся в результате предшествующего
e-захвата. из возбужденных состояний,
образующихся в результате предшествующего
e-захвата.
Последующие эксперименты подтвердили
этот вывод. В табл. 11.3 приведены некоторые
изотопы, для которых наблюдалось запаздывающее
деление.
Таблица 11.3. Излучатели запаздывающего
деления
Изотоп |
T1/2, мин |
Тип распада |
Pf |
Реакция |
236 Pa |
9.1 |
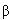 - -
|
10-9 |
238 U( ,np); 238U(d, ,np); 238U(d, ) ) |
238 Pa |
2.3 |
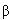 - -
|
10-8 |
238 U(n,p) |
228 Np |
1.0 |
е-захват |
|
209 Bi(22Ne,3n) |
232 Am |
1.0 |
е-захват |
1.3·10-2 |
230 Th(10B,8n); 237Np( ,9n) ,9n) |
234 Am |
2.6 |
е-захват |
8·10-5 |
230 Th(10B,6n) |
240 Bk |
5.0 |
е-захват |
~10-5 |
232 Th(14N,6n) |
244 Es |
0.66 |
е-захват |
2·10-4 |
237 Np(12C,5n) |
246 Es |
7.33 |
е-захват |
4·10-5 |
238 U(14N,6n) |
Так же, как и α-распад, запаздывающее деление возможно
как для нейтронодефицитных ядер (делящееся ядро
получается в результате e-захвата), так и для
нейтроноизбыточных ядер (делящееся ядро
получается в результате β--распада). Исходя из
особенностей процесса запаздывающего деления,
следует ожидать наибольшую вероятность
запаздывающего деления для нечетно-нечетных
ядер, так как в этих случаях энергия 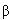 -перехода
увеличивается по сравнению с соседними ядрами.
Большинство обнаруженных в настоящее время
источников запаздывающего деления является
нечетнонечетными изотопами. На вероятность
запаздывающего деления существенное влияние
оказывают как величина (Qb - Qf),
так и форма барьера деления. -перехода
увеличивается по сравнению с соседними ядрами.
Большинство обнаруженных в настоящее время
источников запаздывающего деления является
нечетнонечетными изотопами. На вероятность
запаздывающего деления существенное влияние
оказывают как величина (Qb - Qf),
так и форма барьера деления.
Капельная модель соответствует
усредненному описанию масс атомных ядер и их
формы в зависимости от числа нейтронов и
протонов в ядре и от деформации ядра. Оболочечные
эффекты обычно рассматривались для сферических
ядер. Считалось, что с ростом деформации ядра
из-за расщепления состояний по квантовым числам j
и m происходит существенное увеличение числа
состояний (снятие вырождения по j и m) и
оболочечные эффекты исчезают.
В работах В. Струтинского было
показано, что при изменениях формы ядра
происходит перераспределение плотности уровней,
приводящее к появлению новых оболочек. При этом
некоторые формы ядра могут обладать повышенной
стабильностью. Было показано также, что
изменение полной энергии ядра вокруг
усредненной величины, даваемой капельной
моделью, можно связать с вариацией суммы
одночастичных энергий вблизи границы Ферми. То
есть полная энергия ядра может быть представлена
в виде V = Vкап + Vобол. В то
время как Vкап плавно меняется от ядра к
ядру Vобол может испытывать сильные
флуктуации при небольших изменениях числа
нуклонов в ядре.

Рис. 11.27. Изменение полной энергии ядра в
зависимости от деформации в модели жидкой капли
(штриховая кривая) и с учетом оболочечных
эффектов (сплошная кривая): 1 - быстрое деление; 2 -
запаздывающее деление; 3 - деление из изомерного
состояния; 4 - спонтанное деление |
На рис.11.27 показано, как изменяется
полная энергия ядра в зависимости от деформации
в модели жидкой капли (штриховая кривая) и с
учетом оболочечных эффектов (сплошная кривая).
Существенным является то, что появляются две
потенциальные ямы, разделенные барьером.
Рассмотрим разные случаи, приводящие к
запаздывающему делению.
- Энергия уровня Ei меньше энергии отделения
нейтрона Bn (Ei < Bn). В этом
случае произойдет деление ядра, так как ширина
радиационных переходов в низшие свободные
состояния Гγ
значительно меньше делительной ширины Гf (Гγ << Гf).
- В случае если Ei > Bn, то
вероятность деления с уровня Ei будет
определяться конкуренцией между испусканием
запаздывающих нейтронов и запаздывающим
делением
Wf(Ei) = Гf(Ei)/(Гγ(Ei) + Гf(Ei)).
- Энергия уровня Ei расположена между
энергией второго барьера Eb и энергией
второго минимума Emin. В этом случае деление
происходит из состояний во второй потенциальной
яме. При этом если ядро в результате β-распада сразу
оказывается в состояниях второй потенциальной
ямы, то вероятность запаздывающего деления будут
зависеть от вероятности прохождения через
барьер второй потенциальной ямы. Если ядро после
β-распада
оказывается в состоянии первой потенциальной
ямы, то вначале оно должно в результате γ-перехода
перейти в состояние второй потенциальной ямы и
затем только происходит деление. В результате
исследований механизма запаздывающего деления
сформировалось современное представление о
двугорбом барьере деления, зависимости его
параметров от N и Z, существенном влиянии ядерных
оболочек на энергию деформации ядра.
Смешивание состояний, находящихся в
двух потенциальных ямах, проявляется при
энергиях близких к высоте внутреннего барьера и
при тех энергиях, когда совпадают уровни внешней
и внутренней ямы. Барьер, разделяющий
потенциальные ямы, вызывает сильную
заторможенность γ-переходов из нижних состояний внешней
потенциальной ямы на более низкорасположенные
по энергии состояния во внутренней
потенциальной яме. Заторможенность составляет 1010-1012
по сравнению с обычными переходами с той же
энергией (2-5 МэВ). Для тяжелых ядер деление из
второй потенциальной ямы в некоторых случаях
может оказаться более вероятностным процессом
по сравнению с радиационным распадом.
|

Рис. 11.28. Характеристики барьеров деления Ea
и Eb изотопов плутония, полученные из
анализа данных мгновенного деления и деления
изомеров: кружки - мгновенное деление, квадраты -
деление изомеров; черные - EA, светлые - EB |
На рис. 11.28 показаны характеристики
барьеров деления Ea и Eb изотопов
плутония, полученные из анализа данных
мгновенного и запаздывающего делений. Из этих
данных видно, что высота внешнего барьера Eb
изотопов Pu с массовым числом A < 235 должна
быть меньше 4 МэB.
Изучение вероятностей запаздывающего деления
и деления из изомерного состояния позволило
сделать следующие выводы об изменении формы
барьера деления.
- Высота внутреннего барьера Ea и энергия
минимума Ei слабо меняются в области ядер от
Th до Bk и составляют, соответственно 5.5-6.5 МэВ и
2-3 МэВ.
- Высота внешнего барьера Eb уменьшается с
ростом Z от 6.5 МэВ для Th (Z = 90) до 4 МэВ для
Bk (Z = 97).
Спонтанное деление изомеров обнаружено в 1961
году, когда был открыт первый спонтанно делящийся
изомер 242Am с периодом полураспада 14 мс. В
табл. 11.4 приведены периоды полураспада некоторых
обнаруженных в настоящее время
спонтанноделящихся изомеров.
Таблица 11.4. Периоды полураспада
спонтанно делящихся изомеров
| Изомер |
236U |
238U |
235Pu |
236Pu |
238Pu |
239Pu |
240Pu |
241Pu |
241Cm |
243Cm |
| T1/2, нс |
110 |
200 |
20 |
34 |
6.5 |
8·103 |
4.4 |
27·103 |
19 |
38 |
|

Рис. 11.29. Периоды полураспада спонтанного
деления изомерных (нижняя группа точек) и
основных состояний (верхняя группа точек)
различных изотопов ядер от U до Cm |
На рис. 11.29 показаны периоды
полураспада спонтанного деления изомерных
(нижняя группа точек) и основных состояний
(верхняя группа точек) различных изотопов ядер от
U до Cm. Для спонтанно делящихся изомеров
характерно увеличение вероятности деления в 1020-25
раз. Этот результат не связан просто с
увеличением проницаемости барьера деления с
ростом энергии возбуждения ядра. Наблюдаемые
особенности были объяснены на основе модели
двугорбого барьера деления, развитой в работах
В. Струтинского. Основные закономерности
деления атомных ядер достаточно хорошо
описываются в рамках капельной модели с учетом
оболочечных поправок.
![[Содержание]](../react/images/sod.gif) ![[Экзотические распады]](../introduction/images/next.gif)

|




 Рис. 11.21. Полная множественность
нейтронов в зависимости от энергии возбуждения,
реализующейся при делении
Рис. 11.21. Полная множественность
нейтронов в зависимости от энергии возбуждения,
реализующейся при делении Рис. 11.22. Множественность
предделительных нейтронов в зависимости от
энергии возбуждения компаунд-системы
Рис. 11.22. Множественность
предделительных нейтронов в зависимости от
энергии возбуждения компаунд-системы





