Двухчастичные корреляции заряженных частиц

    Изучение корреляций при множественном рождении частиц позволяет более детально сравнивать различные модели множественного рождения и генераторы частиц. Эффективность исследования двухчастичных корреляций была показана в экспериментах при меньших энергиях и для разных типов сталкивающихся частиц.  Моделирование корреляционных эффектов в инклюзивных реакциях множественного рождения должно включать процессы фрагментации, распады резонансов, многопартонные взаимодействия и рождение струй. Измерение корреляций в соударениях протонов необходимо и потому, что позволяет при столкновениях тяжелых ионов путем сравнения выделить эффекты множественных взаимодействий партонов и присутствия горячей и плотной среды.
    Двухчастичные корреляции заряженных частиц были измерены в эксперименте ATLAS в протонных соударениях при энергиях √s = 0.9 и 7 ТэВ от переменных псевдобыстроты η и азимутального угла φ [1]. Корреляционная функция F(n_ch, Δη, Δφ) зависит от расстояний в паре частиц по псевдобыстроте Δη, азимутальному углу Δφи множественности частиц в событии n_ch  (≥ 2) и выражается следующим образом: 

.

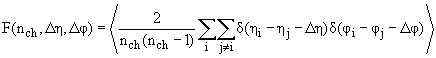   Суммирование проводится по частицам i и j в событии, дельта-функции отбирают пары  с заданными Δη и Δφ, множитель перед суммированиями учитывает число парных комбинаций при множественности n_ch, равное n_ch∙(n_ch-1)/2.  Его присутствие уравнивает статистически вклады от событий с малой и большой множественностью в корреляционную функцию. Плотность заряженных частиц по η практически равномерная и распределение по Δηимеет вид максимума с вершиной при Δη = 0 и линейно падающими сторонами к значениям  Δη = ±η_max. Поэтому вводится функция фона В(n_ch, Δη, Δφ), аналогичная F(n_ch, Δη, Δφ), но учитывающая особенности одночастичных распределений по η при заданном n_chи кинематические границы области измерений. При заданном n_ch корреляционная функция С(n_ch, Δη, Δφ),  будет выражаться как

Значения С(n_ch, Δη, Δφ) по распределению n_ch усредняются с весом (n_ch-1), а затем делятся на полученную усреднением по n_ch  фоновую функцию В(Δη, Δφ). В результате получаем усредненную по распределению по множественности не зависящую от n_ch двухчастичную корреляционную функцию

    На практике величину ‹(n_ch-1)F(n_ch, Δη, Δφ)›_ch  получают выбирая из каждого события все пары частиц, вычисляют расстояния в паре Δη и Δφ и заполняют квадрант двумерного распределения по Δη и Δφ с весом 2/n_ch. Остальные три квадранта заполняются путем отражения относительно (0,0), делая распределение симметричным. Фон определяется выбором пар из разных событий и заполнением другого двумерного распределения,  которое затем нормируется на единичный интеграл. Проекции двухмерной корреляционной функции на переменные Δηи Δφ позволяют более детально исследовать структуру распределений. При этом проекции сначала интегрируются и нормируются на n_ch., а затем берется отношение функции F к В.
    На рис.5.1 приведены измеренные функции R(Δη,Δφ) для рр взаимодействий при энергиях 0.9 и
7 ТэВ. Распределения показывают отчетливый максимум при (Δη,Δφ)= (0,0) и «хребет» в распределении по Δφпри  Δη ~ 0. Максимум распределения более выражен при большей энергии
7 ТэВ. 

 
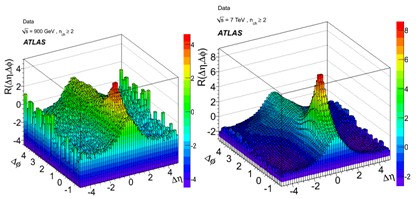
Рис.5.1. Двумерные корреляционные функции заряженных частиц в событиях с n_ch ≥ 2 при энергии  √s = 0.9 (слева) и 7 ТэВ (справа).

На следующих рисунках корреляционные функции при 7 ТэВ сравниваются с модельными расчетами для проекций распределений по Δη и Δφ. Функция R(Δη), проинтегрированная по разности азимутальных углов Δφменьше π/2, показана на рис.5.2 слева и проинтегрированная по Δφ  от π/2 до π показана справа. В нижней части рисунков приведены разности модельных распределений и экспериментальных значений. Большая часть расчетов качественно воспроизводит вид корреляционной функции, но не достигает по величине в её максимуме. Корреляционный максимум наблюдается как для пар частиц, вылетающих в одну полусферу по азимутальному углу, так и для пар, вылетающих в противоположные полусферы.  

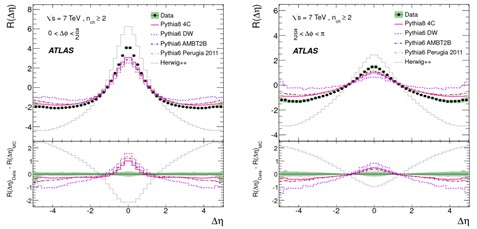
Рис.5.2. Корреляционные функции R(Δη) для пар частиц с Δφменьше π/2 (слева) и пар с Δφ  от π/2 до π (справа) для рр соударений при 7 ТэВ с n_ch≥ 2. Линиями показаны предсказания моделей.

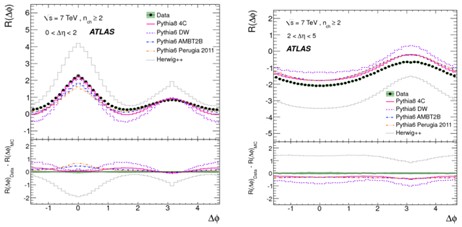
Рис.5.3. Корреляционные функции R(Δφ) для пар частиц с Δη< 2 (слева) и пар удаленных по η частиц с 2 < Δη < 5 (справа) для рр соударений при 7 ТэВ с n_ch≥ 2. Линиями показаны предсказания моделей.

    Корреляционная функция R(Δφ) показана на рис.5.3. Видно, что характер корреляций по азимутальным углам различается для близких по псевдобыстроте частиц (с  Δη < 2) и удаленных
(с 2 < Δη < 5). Удаленные частицы вылетают преимущественно в  противоположных направлениях по азимутальному углу (Δφ ≈ π). Характер распределений в целом воспроизводится в моделях. Характер корреляционных функций не меняется для выборки событий с n_ch≥ 20. Количественные отличия модельных распределений n_ch ≥ 2 могут происходить из-за некорректного учета дифракционных взаимодействий.
    В эксперименте CMS для корреляционной функции в рр взаимодействиях очень большой множественности n_ch ≥ 100 и  частиц с большими РТ при 7 ТэВ впервые наблюдался «хребет» по Δηпри Δφ ≈ 0, который до этого наблюдался только в соударениях тяжелых ионов.

Коллективные корреляции

    Существующие генераторы событий не настраиваются на описание двухчастичных корреляций по псевдобыстроте, поэтому более детальный анализ корреляционных явлений может способствовать дальнейшему их отбору. В эксперименте ATLAS в протонных соударениях при энергиях
√s = 0.9 и 7 ТэВ выполнен анализ корреляций между множественностью заряженных частиц в интервалах псевдобыстроты, симметричных относительно η = 0. Такие корреляции получили название FB-корреляций (вперед-назад корреляции). Помимо множественности частиц, впервые измерены корреляции между суммарными поперечными импульсами заряженных частиц в таких интервалах [2]

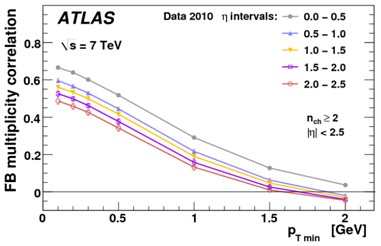Рис.5.4. FB-корреляции множественности заряженных частиц для разных интервалов по псевдобыстроте η между полусферами по и против направления пучка в зависимости от порога поперечного импульса заряженных частиц [2].

    В анализе было найдено, что FB-корреляции становятся слабее при увеличении интервала η между выбранными промежутками псевдобыстроты. Этот результат приведен на рис.5.4. Корреляции ведут себя подобным образом при увеличении порогового значения поперечного импульса заряженных частиц. При 7 ТэВ корреляции существенно увеличиваются для больших интервалов по отношению к данным при 0.9 ТэВ. Стандартные Монте-Карло генераторы недооценивают найденные корреляции на 15% при 7 ТэВ и еще значительнее при
0.9 ТэВ.
    Азимутальные корреляции относительно лидирующей по р_Т частицы в событии показывают еще более заметные расхождения с предсказаниями Монте-Карло генераторов. Расхождения велики как для ближайшей к лидирующей частице области азимутальных углов, так и для противоположной по отношению к лидирующей частице полусферы.
    Форма событий, выраженная в коллективных переменных сферичности и траста в зависимости от поперечного импульса р_Т лидирующей заряженной частицы, представлена в [3] для рр взаимодействий при энергии 7 ТэВ. Эти переменные характеризуют потоки импульсов части в событии. Их поведение чувствительно к процессам, описывающимся как в пертурбативной, так и непертурбативной квантовой хромодинамике. Их использование в анализе формы событий в процессе е⁺е⁻-аннигиляции способствовало выделению трех струйных событий и открытию глюона.
    В эксперименте использовались события с числом заряженных частиц n_ch ≥ 6 и │η│ < 2.5.  Наиболее широко используемая переменная поперечного траста Т_┴ определяется для каждого события следующим образом:

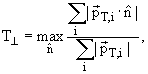
 где суммирование проводится по всем векторам поперечных импульсов частиц i. Вектор n_T определяет направление оси траста, задающейся единичным вектором  n, для которого величина Т_┴ максимальна. Для полностью сбалансированного по р_Т события в форме «карандаша» как образа рождения двух струй  величина Т_┴ = 1. Для равномерного в азимутальной плоскости разлета частиц величина Т_┴ = 2/π. Для удобства представления используется величина τ_┴, равная 0 для чисто двух струйного события.
    Переменная сферичности S определяет поток импульса в событии через тензор

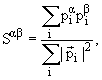
 где символы α, β представляют поперечную x,y и продольную  z компоненты импульса частицы i. Значения сферичности меняются от 0 до 1, для двух струйного события S = 0 и для изотропного S = 1. Для БАК более удобно использовать переменную поперечной сферичности S_┴, которая определяется в плоскости x,y:

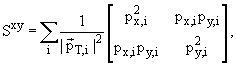
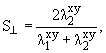
где λ₂^xy < λ₁^xyсобственные векторы  S^xy.
    Анализ выполнялся для событий с разными значениями наибольшего поперечного импульса частицы в событии р_Т^lead,  или лидирующей частицы. Было получено, что форма событий существенно зависит от величины р_Т^lead. На рис.5.5 и 5.6 приведены распределения событий по τ_┴ и  S_┴ для событий, в которых р_Т^lead минимальна и имеет величину 0.5-2.5 ГэВ/с и максимальна с значениями р_Т^lead ≥ 10 ГэВ/с. Из рисунков видно, что форма событий существенно меняется при увеличении р_Т лидирующей в событии частицы.

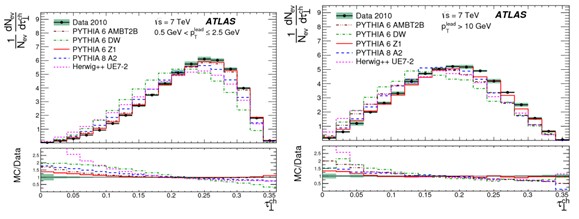
Рис.5.5. Распределения по переменной τ_┴ (см. текст) для событий с р_Т^lead 0.5-2.5 ГэВ/с (слева) и значениями р_Т^lead ≥ 10 ГэВ/с (справа). Символ ch у переменных означает использование в анализе только заряженных частиц.

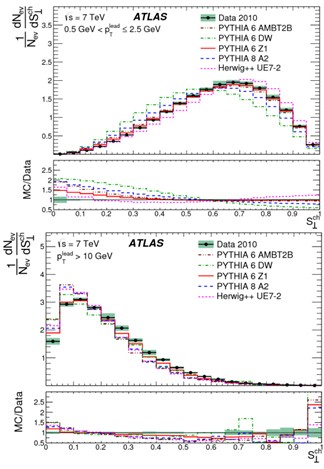
Рис.5.6. Распределения по переменной S_┴(см. текст) для событий с р_Т^lead 0.5-2.5 ГэВ/с (верхний рисунок) и значениями р_Т^lead ≥ 10 ГэВ/с (нижний рисунок). Символ ch у переменных означает использование в анализе только заряженных частиц.

Сопутствующие события (UE)

    Для прецизионной проверки Стандартной модели и поиска явлений новой физики важно не только правильно описывать процессы жесткого рассеяния, происходящие при соударениях протонов на малых расстояниях, но и «мягкие» взаимодействия на больших расстояниях, которые происходят между фрагментами протонов, не участвовавших в жестком рассеянии. Продукты эволюции таких фрагментов принято называть «сопутствующими событиями», underlying events (UE). Разделить жесткие и сопутствующие события в конкретном случае невозможно, но можно выделить такие характеристики события, которые будут чувствительны именно к  сопутствующим событиям, или для сокращения UE-события. В общем случае,  UE-события содержат продукты и жестких, и «мягких» рассеяний с малыми переданными импульсами. Процессы с малыми переданными импульсами описываются генераторами событий. Для  описания процессов рождения струй в жестких соударениях необходимо, чтобы генераторы событий были правильно настроены для воспроизведения как инклюзивных характеристик (или событий с минимальным отбором, minimum bias), так и сопутствующих событий. Для определения UE-событий используется выделенное направление в пространстве переменных η и φ, соответствующее направлению вылета лидирующей частицы (leading particle) с максимальным в событии поперечным импульсом р_Т.  На рис.5.7 слева показано направление вылета лидирующей частицы в азимутальной плоскости и определение областей относительно этого направления с разной чувствительностью к UE-событиям:

1. Δφ│  < 60° - область сопровождения (toward);
2. 60° < │Δφ│< 120° - поперечная область (transverse);
3. Δφ│> 120° - область компенсации (away).

 
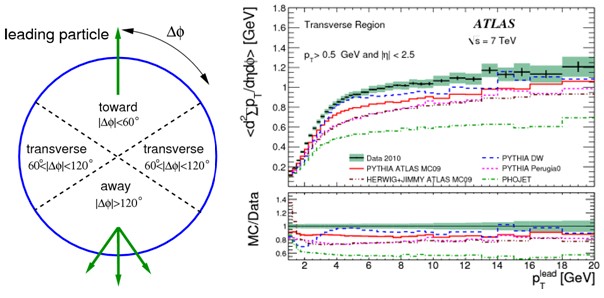
Рис.5.7. Определение областей в азимутальной плоскости для поперечной области сопутствующих событий – слева; зависимость плотности d²N_ch/dηdφ для заряженных частиц с р_Т > 0.5 ГэВ/с и
│η│ < 2.5 от величины р_Т^lead – справа для рр соударений при 7 ТэВ. Кривые показывают предсказания генераторов событий.

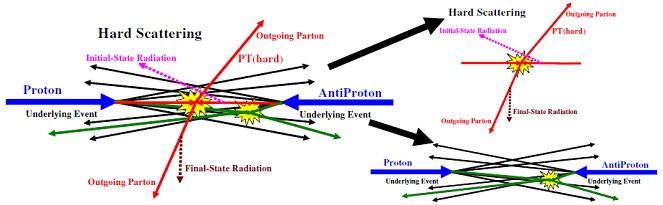
Рис.5.7а. Схема соударения протона и антипротона с жестким рассеянием, включая излучение в начальном и конечном состоянии (hard scattering with Initial-state and Final-state radiation), и сопутствующим событием [7].

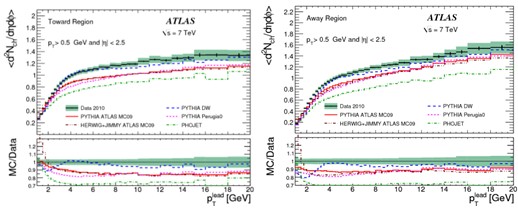
Рис.5.8 Плотности d²N_ch/dηdφ для заряженных частиц с р_Т > 0.5 ГэВ/с и │η│ < 2.5 от величины р_Т^lead  для областей сопровождения (слева) и компенсации (справа) для рр соударений при 7 ТэВ. Кривые показывают предсказания генераторов событий.

    Значения d²N_ch/dηdφ на рис.5.7 для поперечной области увеличиваются вдвое при изменении р_Т^lead от 2 до 5 ГэВ/с, а затем практически не меняются по величине, составляя  величину ~0,8. Если предположить, что эта плотность равномерна по φ, то множественности dN_ch/dη, интегрированной по φ, соответствует значение, равное 5. Эту величину можно сравнить с измеренной величиной dN_ch/dη для событий с минимальным отбором 2.432±0.001±0.042 для р_Т > 0.5 ГэВ/с и убедиться, что множественность заряженных частиц в сопутствующих событиях с лидирующей частицей с р_Т^lead от 2 до 5 ГэВ/с вдвое превышает множественность в событиях с минимальным отбором. Очевидно, что этот эффект вызван присутствием жесткого рассеяния в отобранных событиях, отсутствием вклада дифракционных событий и того факта, что в событиях с жестким рассеянием более вероятны многопартонные взаимодействия (multiparton interactions, MPI). Присутствие таких взаимодействий было отмечено на коллайдере Теватрон, но столь значительное их проявление было обнаружено при энергиях БАК.  Активность в сопутствующих событиях оказалась на ~15% выше, чем предсказания генераторов событий, настроенных на данных Теватрона.  Сравнение результатов эксперимента ATLAS при 0.9 и 7 Тэв показало, что множественность сопутствующих событий возросла с энергией в два раза. Если плотность частиц выходит на плато для поперечной области на рис.7 (справа), то для областей сопровождения и компенсации, данные для которых при 7 ТэВ показаны на рис.8, плато не наблюдается. Множественности непрерывно растут, следуя возрастанию энергии струй. Аналогичная картина наблюдается и при 0.9 ТэВ.
    Поведение величин d²Σр_Тch/dηdφ и <р_Т> от величины р_Т^lead оказалось подобным поведению множественности для всех трех областей.
    В эксперименте ATLAS характеристики сопутствующих событий были измерены также с помощью системы калориметров. Измеряемые потоки энергии относительно лидирующей частицы включают вклад как от заряженных, так и нейтральных частиц [5]. Результаты подтвердили закономерности, найденные при анализе заряженных частиц [4]. На рис. 5.9 приведены d²N_ch/dηdφ и d²Σр_Тch/dηdφ для рр взаимодействий при энергии 7 ТэВ по измерениям в калориметрах.

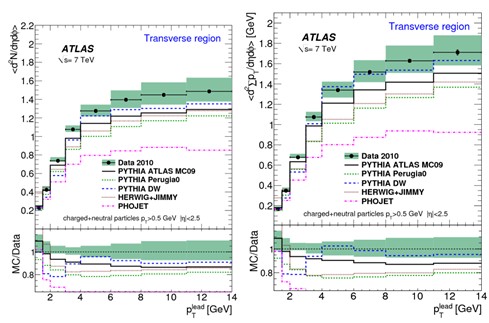
Рис.5.9. Зависимости d²N_ch/dηdφ (слева) и d²Σр_Тch/dηdφ (справа) для рр взаимодействий при энергии 7 ТэВ по измерениям кластеров с р_Т > 0.5 ГэВ/с и │η│ < 2.5   в калориметрах для нейтральных и заряженных частиц [5].

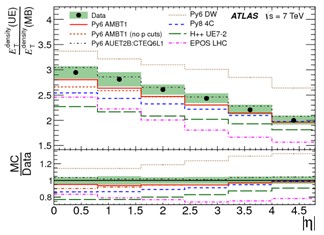
Рис.5.10. Отношение потоков поперечной энергии Е_Т в сопутствующих событиях UE с рождением двух струй  к потоку Е_Т в событиях с минимальным отбором (MB) в диапазоне │η│ < 4.8 в рр взаимодействиях при 7 ТэВ [6].

Литература к разделу 5

1. Measurement of inclusive two-particle angular correlations in pp collisions with the ATLAS detector at the LHC, ATLAS Collaboration, JHEP 1205 (2012)157.
2. Forward-backward correlations and charged-particle azimuthal distributions in pp interactions using the ATLAS detector, ATLAS Collaboration, JHEP 1207 (2012)019.
3. Measurement of charged-particle event shape variables in inclusive √ s = 7 TeV proton–proton interactions with the ATLAS detector, ATLAS Collaboration, Phys.Rev.D 88, 032004 (2013)
4. Measurement of underlying event characteristics using charged particles in pp collisions at √s = 900 GeV and 7 TeV with the ATLAS detector, ATLAS Collaboration, Phys.Rev.D83 (2011)112001.
5. Measurements of underlying-event properties using neutral and charged particles in pp collisions at 900 GeV and 7 TeV with the ATLAS detector at the LHC, ATLAS Collaboration, Eur.Phys.J. C71 (2011)1636.
6. Measurements of the pseudorapidity dependence of the total transverse energy in proton-proton collisions at  √s=7 TeV with ATLAS, ATLAS Collaboration, JHEP11(2012)033.
7. Studying the underlying event in Drell-Yan and high transverse momentum jet production at the Tevatron, T.Aaltonen et al., CDF Collaboration, Phys.Rev.D82, 034001 (2010).