< Previous | Contents | Next >
По современным представлениям образование подавляющего числа тяже- лых изотопов в природе происходит за счет звездного r-процесса. Это малоизу- ченный механизм, требующий экстремальных внешних условий, возможных, например, на взрывных стадиях звездной эволюции или при столкновении ком- пактных астрофизических объектов, таких как нейтронные звезды. Между тем исследование этого явления чрезвычайно важно, так как оно непосредственно влияет на распространенность изотопов во Вселенной.
Основным методом исследования r-процесса и эволюции астрофизических ядерных систем в целом является математическое моделирование. Для получе- ния надежных результатов симуляции необходимо достоверно знать ряд вход- ных параметров, таких как состав звездного вещества, его температуры и плот- ности, а также сечения ядерных реакций, протекающих в звездах. На данный момент эти величины известны в основном из теоретических моделей, астро- физических и ядерных, что вызывает существенные неопределенности входных данных.
Трудность вызывает также и сам расчет эволюции ядерных систем, целью которого является получение конечных массовых распределений изотопов за время эволюции системы. С математической точки зрения эта задача оказыва- ется достаточно нестандартной, большинство отработанных численных методов к ней неприменимы. Проблема поиска быстрой и точной расчетной схемы для симуляции процессов естественного нуклеосинтеза, которую можно было бы внедрить в полномасштабные системы астрофизического моделирования, все еще остается актуальной.
Настоящая работа посвящена компьютерному расчету r-процесса и других механизмов звездного нуклеосинтеза. Раздел 1 дает краткий обзор астрофизи- ческого нуклеосинтеза, описывает принцип и сценарии r-процесса и обосновы- вает важность этого механизма. В разделе 2 рассматривается влияние, оказы- ваемое на точность результатов моделирования факторами неопределенности входных данных о сечениях ядерных реакций на нейтроноизбыточных ядрах. В разделе 3 исследуются численные схемы решения систем обыкновенных диф- ференциальных уравнений повышенной жесткости, которые возникают при мо- делировании процессов звездного нуклеосинтеза, рассматривается возможность применения ряда новых методов, с помощью которых можно было бы сократить трудоемкость расчета.

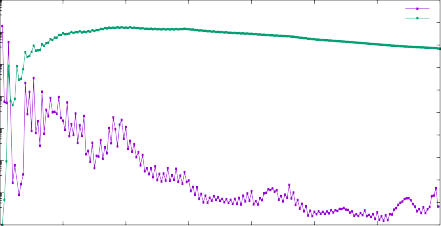
Отн. концентрация Энергия связи
1012 10
Относительная концентрация, N(Si) = 16
9
Удельная энергия связи, МэВ/нуклон
1010
8
108 7
106 6
5
104
4
102 3
2
100
1
10-2
0
30 60 90 120 150
Массовое число
180
0
210